The LAB

Chapter 1. Vectors, scalars, and geometry

1. Scalars, Vectors, and Coordinate Systems

Let’s get our hands dirty! This lab is about playing with the building blocks of linear algebra: scalars and vectors. Think of a scalar as just a plain number, like 3 or -1.5. A vector is a small list of numbers, which you can picture as an arrow in space.

We’ll use Python (with NumPy) to explore them. Don’t worry if this is your first time with NumPy - we’ll go slowly.

Set Up Your Lab

import numpy as np

That’s it - we’re ready! NumPy is the main tool we’ll use for linear algebra.

Step-by-Step Code Walkthrough

Scalars are just numbers.

a = 5       # a scalar
b = -2.5    # another scalar

print(a + b)   # add them
print(a * b)   # multiply them

2.5
-12.5

Vectors are lists of numbers.

v = np.array([2, 3])      # a vector in 2D
w = np.array([1, -1, 4])  # a vector in 3D

print(v)
print(w)

[2 3]
[ 1 -1  4]

Coordinates tell us where we are. Think of [2, 3] as “go 2 steps in the x-direction, 3 steps in the y-direction.”

We can even draw it:

import matplotlib.pyplot as plt

# plot vector v
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(0, 4)
plt.ylim(0, 4)
plt.grid()
plt.show()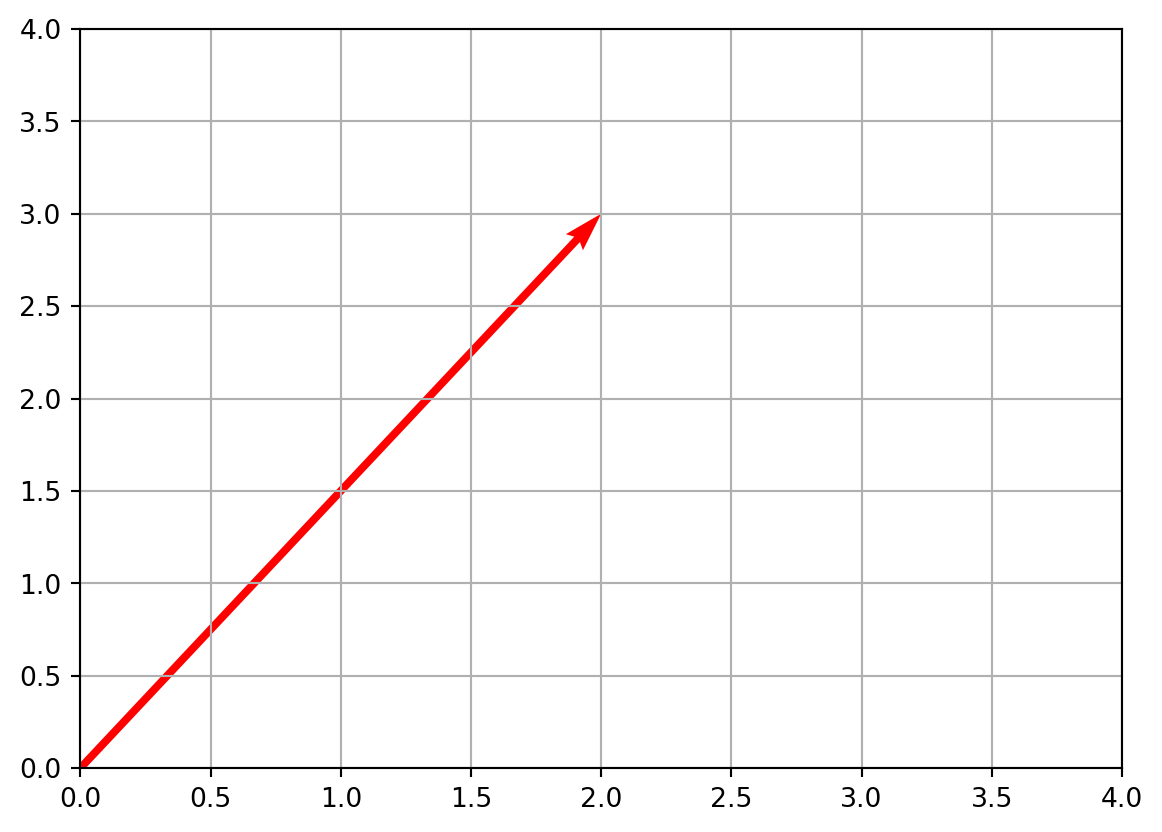

This makes a little arrow from the origin (0,0) to (2,3).

Try It Yourself

1. Change the vector v to [4, 1]. Where does the arrow point now?
2. Try making a 3D vector with 4 numbers, like [1, 2, 3, 4]. What happens?
3. Replace np.array([2,3]) with np.array([0,0]). What does the arrow look like?

2. Vector Notation, Components, and Arrows

In this lab, we’ll practice reading, writing, and visualizing vectors in different ways. A vector can look simple at first - just a list of numbers - but how we write it and how we interpret it really matters. This is where notation and components come into play.

A vector has:

• A symbol (we might call it v, w, or even →AB in geometry).
• Components (the individual numbers, like 2 and 3 in [2, 3]).
• An arrow picture (a geometric way to see the vector as a directed line segment).

Let’s see all three in action with Python.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Writing vectors in Python

# Two-dimensional vector
v = np.array([2, 3])

# Three-dimensional vector
w = np.array([1, -1, 4])

print("v =", v)
print("w =", w)

v = [2 3]
w = [ 1 -1  4]

Here v has components (2, 3) and w has components (1, -1, 4).

2. Accessing components Each number in the vector is a component. We can pick them out using indexing.

print("First component of v:", v[0])
print("Second component of v:", v[1])

First component of v: 2
Second component of v: 3

Notice: in Python, indices start at 0, so v[0] is the first component.

3. Visualizing vectors as arrows In 2D, it’s easy to draw a vector from the origin (0,0) to its endpoint (x,y).

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(-1, 4)
plt.ylim(-2, 4)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()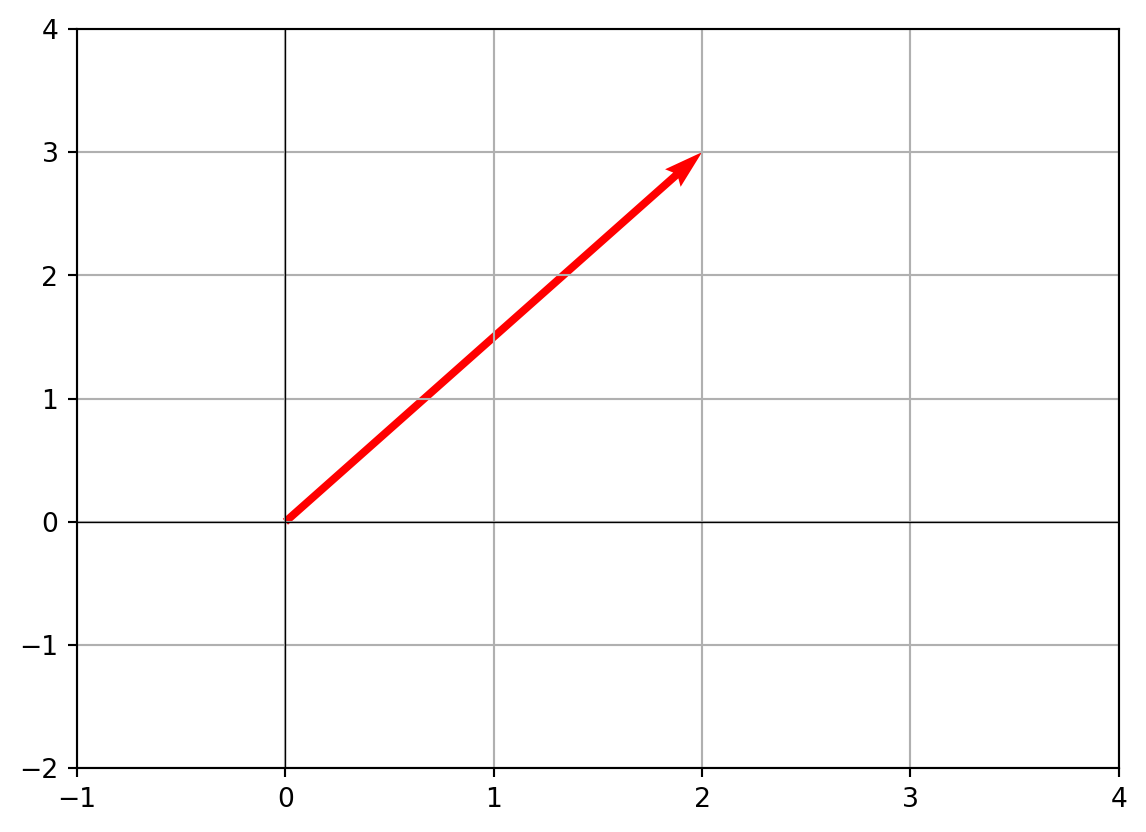

This shows vector v as a red arrow from (0,0) to (2,3).

4. Drawing multiple vectors We can plot several arrows at once to compare them.

u = np.array([3, 1])
z = np.array([-1, 2])

# Draw v, u, z in different colors
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='v')
plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b', label='u')
plt.quiver(0, 0, z[0], z[1], angles='xy', scale_units='xy', scale=1, color='g', label='z')

plt.xlim(-2, 4)
plt.ylim(-2, 4)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()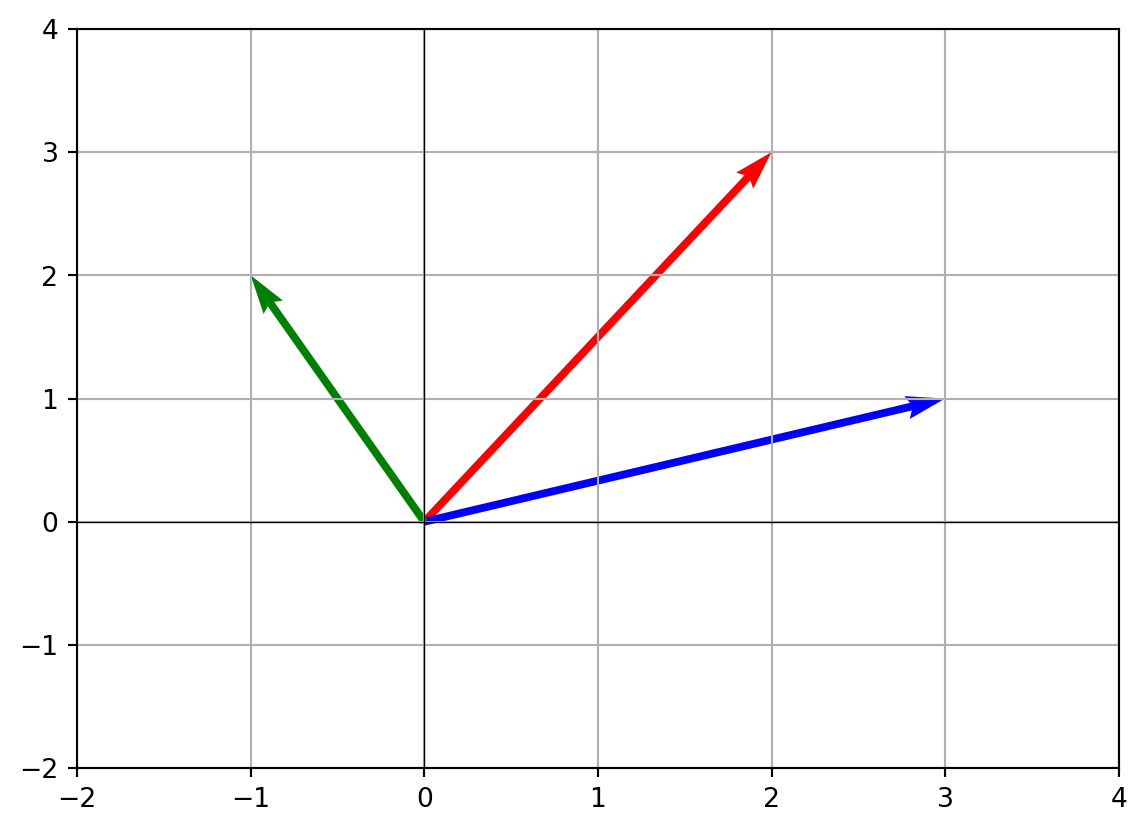

Now you’ll see three arrows starting at the same point, each pointing in a different direction.

Try It Yourself

1. Change v to [5, 0]. What does the arrow look like now?
2. Try a vector like [0, -3]. Which axis does it line up with?
3. Make a new vector q = np.array([2, 0, 0]). What happens if you try to plot it with plt.quiver in 2D?

3. Vector Addition and Scalar Multiplication

In this lab, we’ll explore the two most fundamental operations you can perform with vectors: adding them together and scaling them by a number (a scalar). These operations form the basis of everything else in linear algebra, from geometry to machine learning. Understanding how they work, both in code and visually, is key to building intuition.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Vector addition When you add two vectors, you simply add their components one by one.

v = np.array([2, 3])
u = np.array([1, -1])

sum_vector = v + u
print("v + u =", sum_vector)

v + u = [3 2]

Here, (2,3) + (1,-1) = (3,2).

2. Visualizing vector addition (tip-to-tail method) Graphically, vector addition means placing the tail of one vector at the head of the other. The resulting vector goes from the start of the first to the end of the second.

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='v')
plt.quiver(v[0], v[1], u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b', label='u placed at end of v')
plt.quiver(0, 0, sum_vector[0], sum_vector[1], angles='xy', scale_units='xy', scale=1, color='g', label='v + u')

plt.xlim(-1, 5)
plt.ylim(-2, 5)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()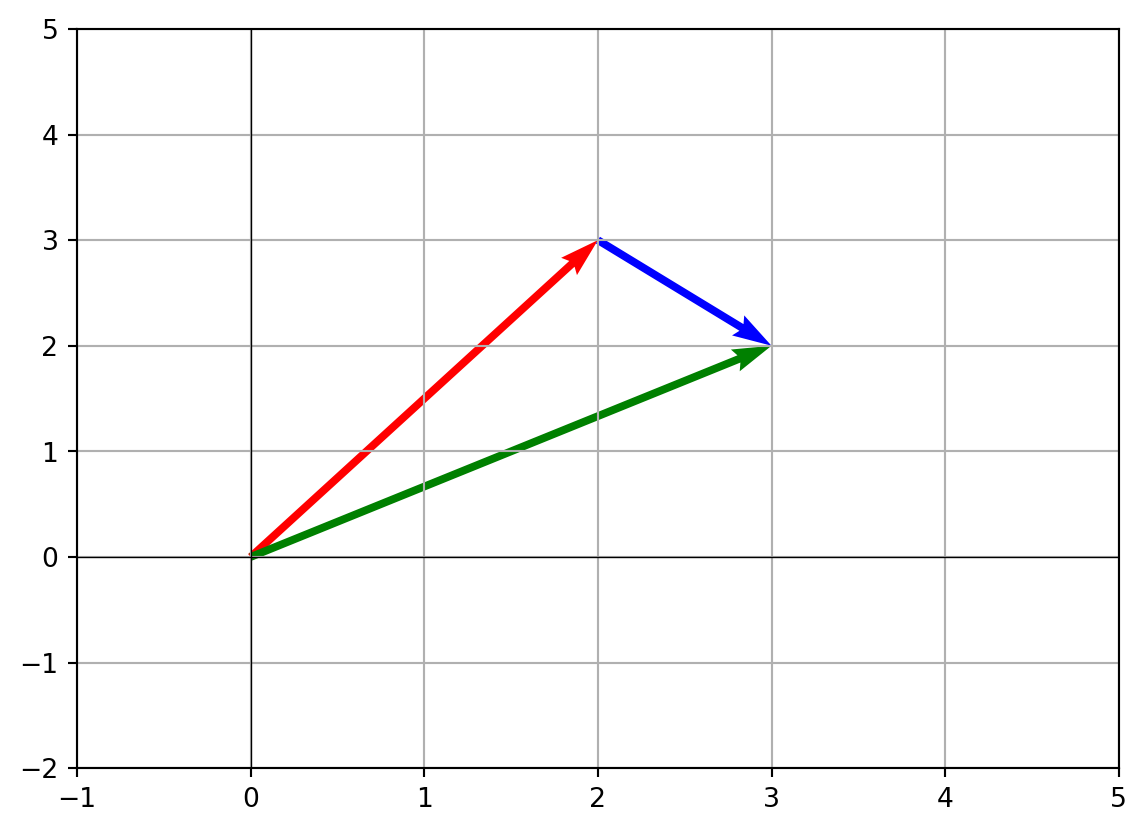

The green arrow is the result of adding v and u.

3. Scalar multiplication Multiplying a vector by a scalar stretches or shrinks it. If the scalar is negative, the vector flips direction.

c = 2
scaled_v = c * v
print("2 * v =", scaled_v)

d = -1
scaled_v_neg = d * v
print("-1 * v =", scaled_v_neg)

2 * v = [4 6]
-1 * v = [-2 -3]

So 2 * (2,3) = (4,6) and -1 * (2,3) = (-2,-3).

4. Visualizing scalar multiplication

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='v')
plt.quiver(0, 0, scaled_v[0], scaled_v[1], angles='xy', scale_units='xy', scale=1, color='b', label='2 * v')
plt.quiver(0, 0, scaled_v_neg[0], scaled_v_neg[1], angles='xy', scale_units='xy', scale=1, color='g', label='-1 * v')

plt.xlim(-5, 5)
plt.ylim(-5, 7)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()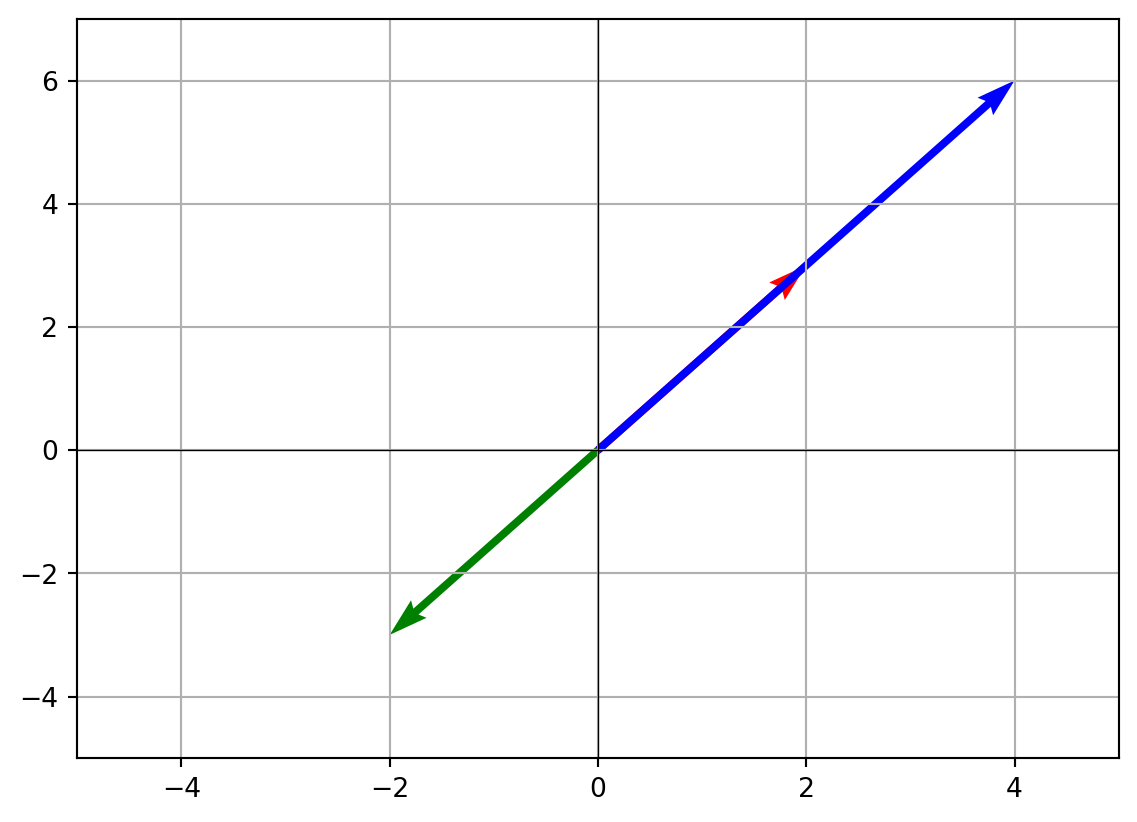

Here, the blue arrow is twice as long as the red arrow, while the green arrow points in the opposite direction.

5. Combining both operations We can scale vectors and then add them. This is called a linear combination (and it’s the foundation for the next section).

combo = 3*v + (-2)*u
print("3*v - 2*u =", combo)

3*v - 2*u = [ 4 11]

Try It Yourself

1. Replace c = 2 with c = 0.5. What happens to the vector?
2. Try adding three vectors: v + u + np.array([-1,2]). Can you predict the result before printing?
3. Visualize 3*v + 2*u using arrows. How does it compare to just v + u?

4. Linear Combinations and Span

Now that we know how to add vectors and scale them, we can combine these two moves to create linear combinations. A linear combination is just a recipe: multiply vectors by scalars, then add them together. The set of all possible results you can get from such recipes is called the span.

This idea is powerful because span tells us what directions and regions of space we can reach using given vectors.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Linear combinations in Python

v = np.array([2, 1])
u = np.array([1, 3])

combo1 = 2*v + 3*u
combo2 = -1*v + 4*u

print("2*v + 3*u =", combo1)
print("-v + 4*u =", combo2)

2*v + 3*u = [ 7 11]
-v + 4*u = [ 2 11]

Here, we multiplied and added vectors using scalars. Each result is a new vector.

2. Visualizing linear combinations Let’s plot v, u, and their combinations.

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='v')
plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b', label='u')
plt.quiver(0, 0, combo1[0], combo1[1], angles='xy', scale_units='xy', scale=1, color='g', label='2v + 3u')
plt.quiver(0, 0, combo2[0], combo2[1], angles='xy', scale_units='xy', scale=1, color='m', label='-v + 4u')

plt.xlim(-5, 10)
plt.ylim(-5, 10)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()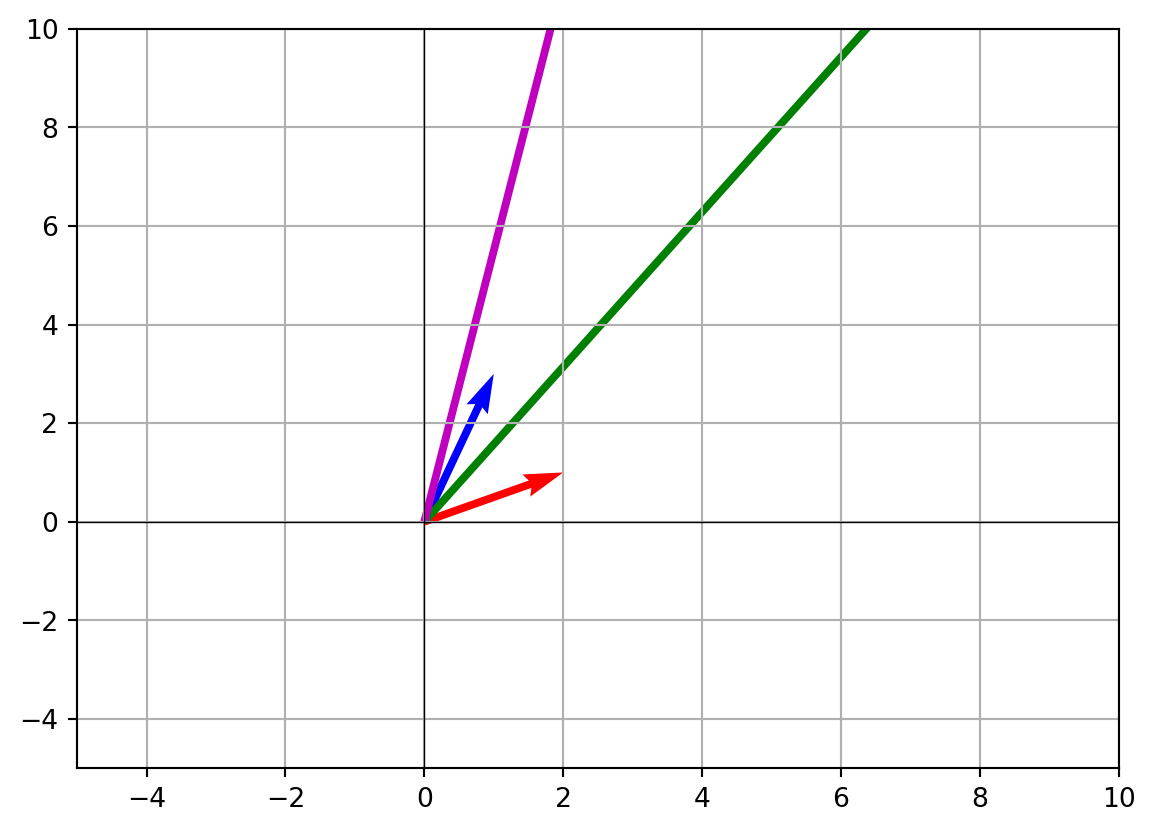

This shows how new arrows can be generated from scaling and adding the original ones.

3. Exploring the span The span of two 2D vectors is either:

• A line (if one is a multiple of the other).
• The whole 2D plane (if they are independent).

# Generate many combinations
coeffs = range(-5, 6)
points = []
for a in coeffs:
    for b in coeffs:
        point = a*v + b*u
        points.append(point)

points = np.array(points)

plt.scatter(points[:,0], points[:,1], s=10, color='gray')
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b')

plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()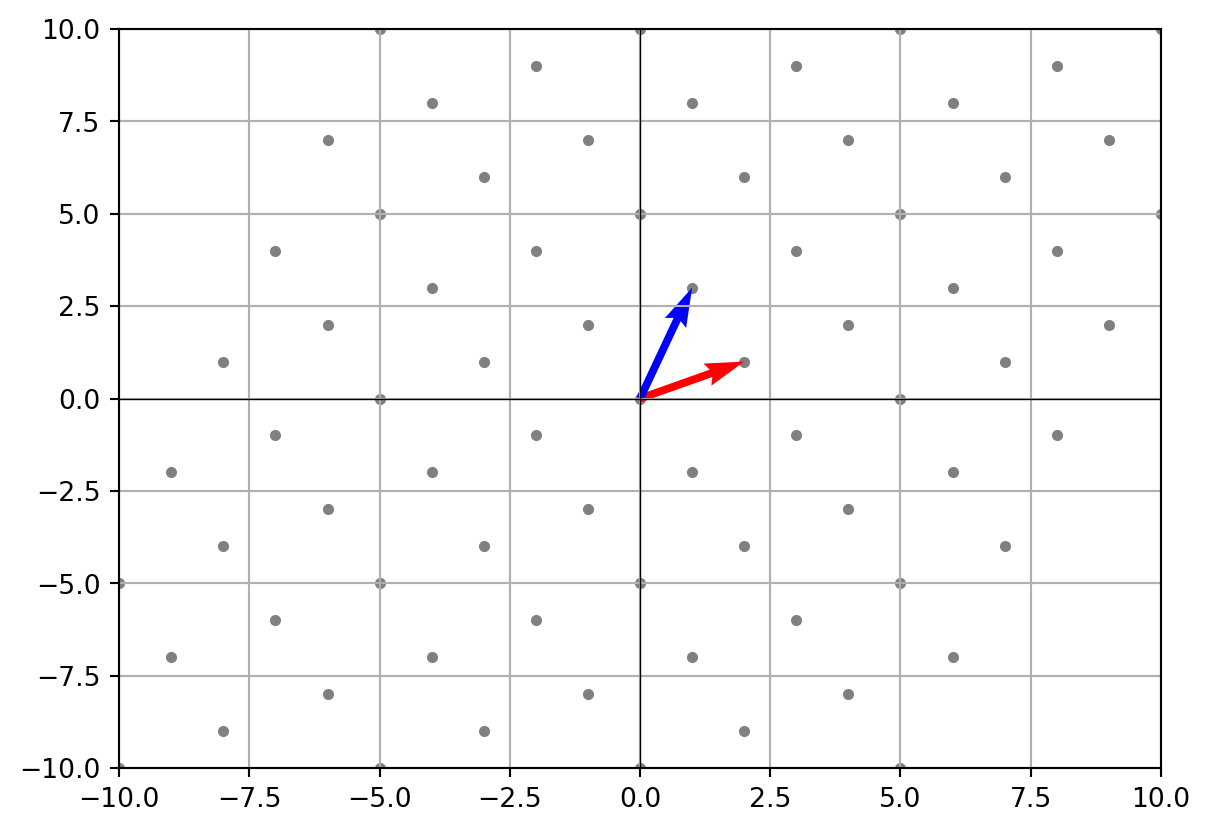

The gray dots show all reachable points with combinations of v and u.

4. Special case: dependent vectors

w = np.array([4, 2])  # notice w = 2*v
coeffs = range(-5, 6)
points = []
for a in coeffs:
    for b in coeffs:
        points.append(a*v + b*w)

points = np.array(points)

plt.scatter(points[:,0], points[:,1], s=10, color='gray')
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.quiver(0, 0, w[0], w[1], angles='xy', scale_units='xy', scale=1, color='b')

plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()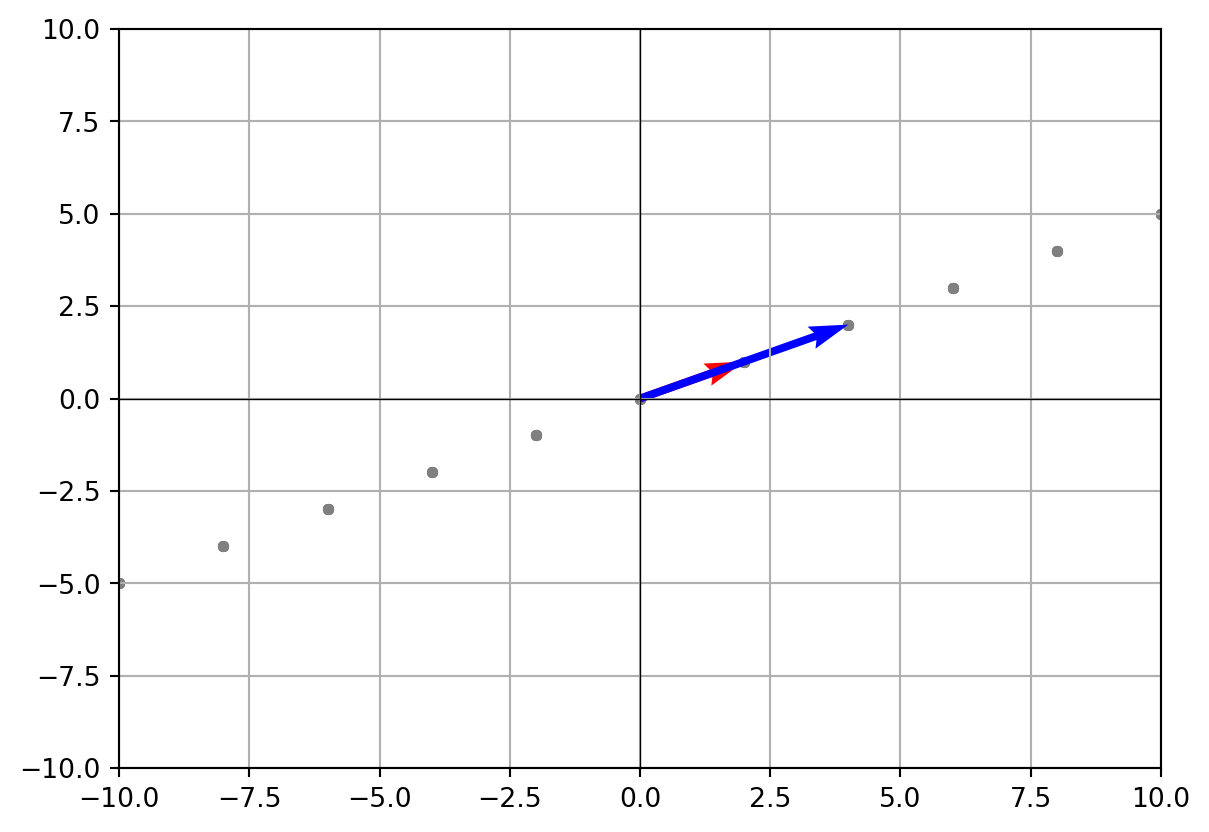

Here, the span collapses to a line because w is just a scaled copy of v.

Try It Yourself

1. Replace u = [1,3] with u = [-1,2]. What does the span look like?
2. Try three vectors in 2D (e.g., v, u, w). Do you get more than the whole plane?
3. Experiment with 3D vectors. Use np.array([x,y,z]) and check whether different vectors span a plane or all of space.

5. Length (Norm) and Distance

In this lab, we’ll measure how big a vector is (its length, also called its norm) and how far apart two vectors are (their distance). These ideas connect algebra to geometry: when we compute a norm, we’re measuring the size of an arrow; when we compute a distance, we’re measuring the gap between two points in space.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Vector length (norm) in 2D The length of a vector is computed using the Pythagorean theorem. For a vector (x, y), the length is sqrt(x² + y²).

v = np.array([3, 4])
length = np.linalg.norm(v)
print("Length of v =", length)

Length of v = 5.0

This prints 5.0, because (3,4) forms a right triangle with sides 3 and 4, and sqrt(3²+4²)=5.

2. Manual calculation vs NumPy

manual_length = (v[0]**2 + v[1]**2)**0.5
print("Manual length =", manual_length)
print("NumPy length =", np.linalg.norm(v))

Manual length = 5.0
NumPy length = 5.0

Both give the same result.

3. Visualizing vector length

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.text(v[0]/2, v[1]/2, f"Length={length}", fontsize=10, color='blue')
plt.grid()
plt.show()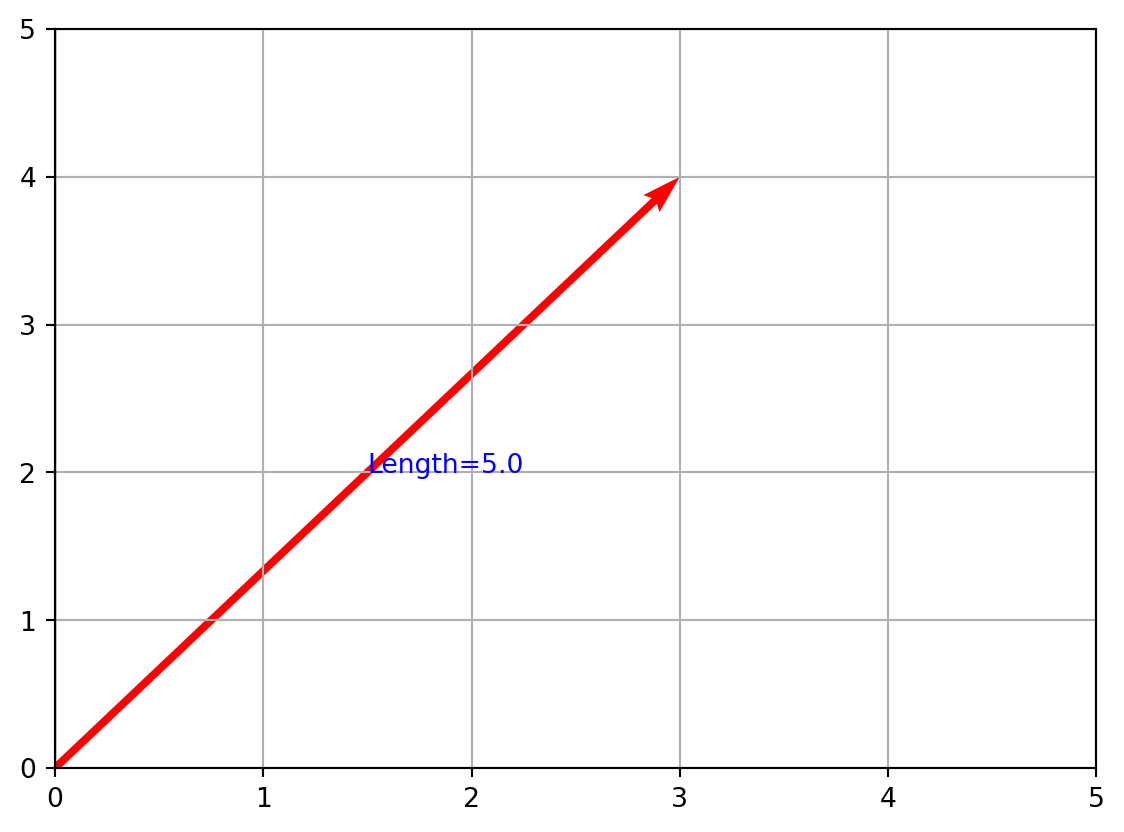

You’ll see the arrow (3,4) with its length labeled.

4. Distance between two vectors The distance between v and another vector u is the length of their difference: ‖v - u‖.

u = np.array([0, 0])   # the origin
dist = np.linalg.norm(v - u)
print("Distance between v and u =", dist)

Distance between v and u = 5.0

Since u is the origin, this is just the length of v.

5. A more interesting distance

u = np.array([1, 1])
dist = np.linalg.norm(v - u)
print("Distance between v and u =", dist)

Distance between v and u = 3.605551275463989

This measures how far (3,4) is from (1,1).

6. Visualizing distance between points

plt.scatter([v[0], u[0]], [v[1], u[1]], color=['red','blue'])
plt.plot([v[0], u[0]], [v[1], u[1]], 'k--')
plt.text(v[0], v[1], 'v', fontsize=12, color='red')
plt.text(u[0], u[1], 'u', fontsize=12, color='blue')
plt.grid()
plt.show()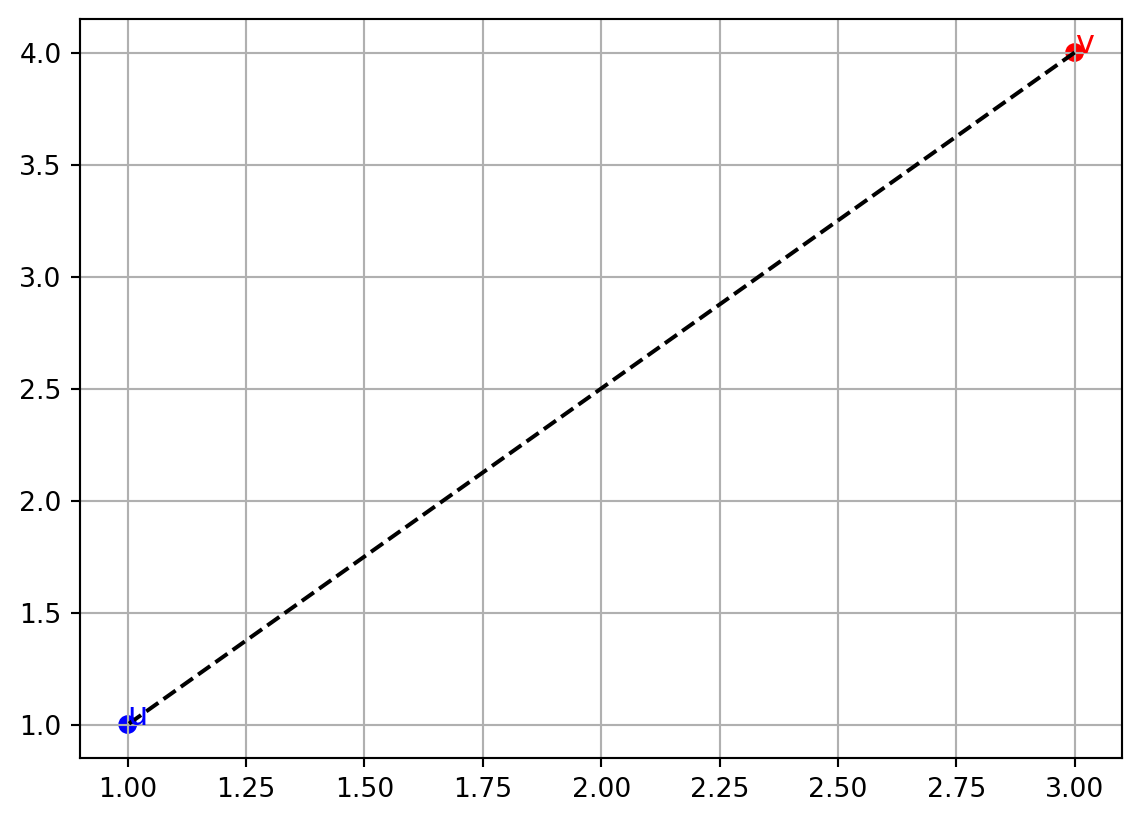

The dashed line shows the distance between the two points.

7. Higher-dimensional vectors Norms and distances work the same way in any dimension:

a = np.array([1,2,3])
b = np.array([4,0,8])
print("‖a‖ =", np.linalg.norm(a))
print("‖b‖ =", np.linalg.norm(b))
print("Distance between a and b =", np.linalg.norm(a-b))

‖a‖ = 3.7416573867739413
‖b‖ = 8.94427190999916
Distance between a and b = 6.164414002968976

Even though we can’t draw 3D easily on paper, the formulas still apply.

Try It Yourself

1. Compute the length of np.array([5,12]). What do you expect?
2. Find the distance between (2,3) and (7,7). Can you sketch it by hand and check?
3. In 3D, try vectors (1,1,1) and (2,2,2). Why is the distance exactly sqrt(3)?

6. Dot Product

The dot product is one of the most important operations in linear algebra. It takes two vectors and gives you a single number. That number combines both the lengths of the vectors and how much they point in the same direction. In this lab, we’ll calculate dot products in several ways, see how they relate to geometry, and visualize their meaning.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Algebraic definition The dot product of two vectors is the sum of the products of their components:

v = np.array([2, 3])
u = np.array([4, -1])

dot_manual = v[0]*u[0] + v[1]*u[1]
dot_numpy = np.dot(v, u)

print("Manual dot product:", dot_manual)
print("NumPy dot product:", dot_numpy)

Manual dot product: 5
NumPy dot product: 5

Here, (2*4) + (3*-1) = 8 - 3 = 5.

2. Geometric definition The dot product also equals the product of the lengths of the vectors times the cosine of the angle between them:

\[ v \cdot u = \|v\| \|u\| \cos \theta \]

We can compute the angle:

norm_v = np.linalg.norm(v)
norm_u = np.linalg.norm(u)

cos_theta = np.dot(v, u) / (norm_v * norm_u)
theta = np.arccos(cos_theta)

print("cos(theta) =", cos_theta)
print("theta (in radians) =", theta)
print("theta (in degrees) =", np.degrees(theta))

cos(theta) = 0.33633639699815626
theta (in radians) = 1.2277723863741932
theta (in degrees) = 70.3461759419467

This gives the angle between v and u.

3. Visualizing the dot product Let’s draw the two vectors:

plt.quiver(0,0,v[0],v[1],angles='xy',scale_units='xy',scale=1,color='r',label='v')
plt.quiver(0,0,u[0],u[1],angles='xy',scale_units='xy',scale=1,color='b',label='u')
plt.xlim(-1,5)
plt.ylim(-2,4)
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.show()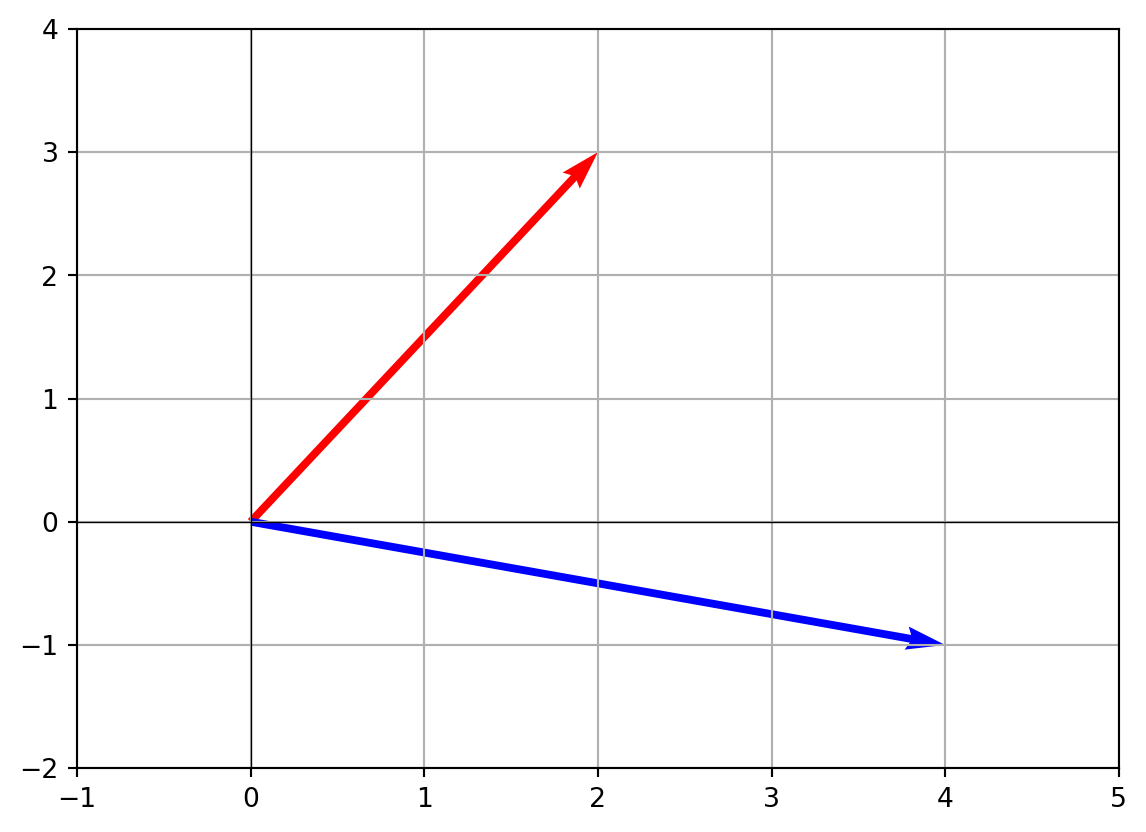

The dot product is positive if the angle is less than 90°, negative if greater than 90°, and zero if the vectors are perpendicular.

4. Projections and dot product The dot product lets us compute how much of one vector lies in the direction of another.

proj_length = np.dot(v, u) / np.linalg.norm(u)
print("Projection length of v onto u:", proj_length)

Projection length of v onto u: 1.212678125181665

This is the length of the shadow of v onto u.

5. Special cases

• If vectors point in the same direction, the dot product is large and positive.
• If vectors are perpendicular, the dot product is zero.
• If vectors point in opposite directions, the dot product is negative.

a = np.array([1,0])
b = np.array([0,1])
c = np.array([-1,0])

print("a · b =", np.dot(a,b))   # perpendicular
print("a · a =", np.dot(a,a))   # length squared
print("a · c =", np.dot(a,c))   # opposite

a · b = 0
a · a = 1
a · c = -1

Try It Yourself

1. Compute the dot product of (3,4) with (4,3). Is the result larger or smaller than the product of their lengths?
2. Try (1,2,3) · (4,5,6). Does the geometric meaning still work in 3D?
3. Create two perpendicular vectors (e.g. (2,0) and (0,5)). Verify the dot product is zero.

7. Angles Between Vectors and Cosine

In this lab, we’ll go deeper into the connection between vectors and geometry by calculating angles. Angles tell us how much two vectors “point in the same direction.” The bridge between algebra and geometry here is the cosine formula, which comes directly from the dot product.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Formula for the angle The angle \(\theta\) between two vectors \(v\) and \(u\) is given by:

\[ \cos \theta = \frac{v \cdot u}{\|v\| \, \|u\|} \]

This means:

• If \(\cos \theta = 1\), the vectors point in exactly the same direction.
• If \(\cos \theta = 0\), they are perpendicular.
• If \(\cos \theta = -1\), they point in opposite directions.

2. Computing the angle in Python

v = np.array([2, 3])
u = np.array([3, -1])

dot = np.dot(v, u)
norm_v = np.linalg.norm(v)
norm_u = np.linalg.norm(u)

cos_theta = dot / (norm_v * norm_u)
theta = np.arccos(cos_theta)

print("cos(theta) =", cos_theta)
print("theta in radians =", theta)
print("theta in degrees =", np.degrees(theta))

cos(theta) = 0.2631174057921088
theta in radians = 1.3045442776439713
theta in degrees = 74.74488129694222

This gives both the cosine value and the actual angle.

3. Visualizing the vectors

plt.quiver(0,0,v[0],v[1],angles='xy',scale_units='xy',scale=1,color='r',label='v')
plt.quiver(0,0,u[0],u[1],angles='xy',scale_units='xy',scale=1,color='b',label='u')

plt.xlim(-1,4)
plt.ylim(-2,4)
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.show()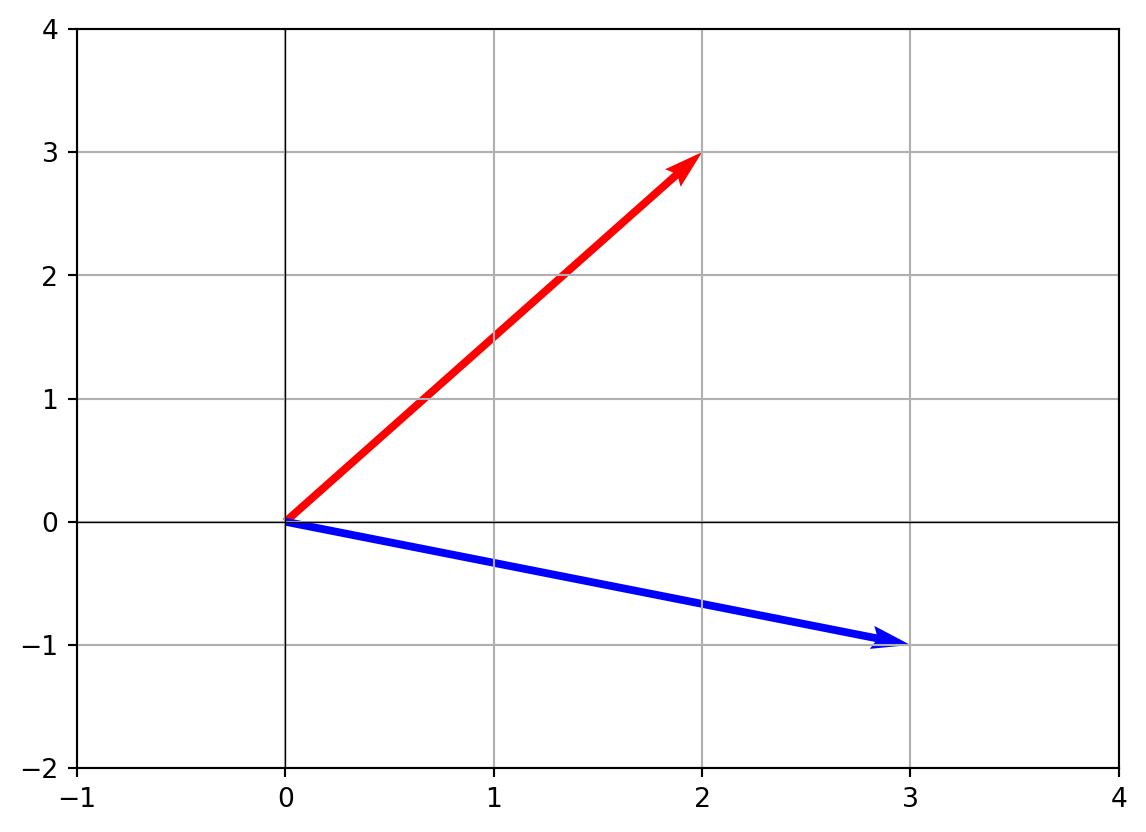

You can see the angle between v and u as the gap between the red and blue arrows.

4. Checking special cases

a = np.array([1,0])
b = np.array([0,1])
c = np.array([-1,0])

print("Angle between a and b =", np.degrees(np.arccos(np.dot(a,b)/(np.linalg.norm(a)*np.linalg.norm(b)))))
print("Angle between a and c =", np.degrees(np.arccos(np.dot(a,c)/(np.linalg.norm(a)*np.linalg.norm(c)))))

Angle between a and b = 90.0
Angle between a and c = 180.0

• Angle between (1,0) and (0,1) is 90°.
• Angle between (1,0) and (-1,0) is 180°.

5. Using cosine as a similarity measure In data science and machine learning, people often use cosine similarity instead of raw angles. It’s just the cosine value itself:

cosine_similarity = np.dot(v,u)/(np.linalg.norm(v)*np.linalg.norm(u))
print("Cosine similarity =", cosine_similarity)

Cosine similarity = 0.2631174057921088

Values close to 1 mean vectors are aligned, values near 0 mean unrelated, and values near -1 mean opposite.

Try It Yourself

1. Create two random vectors with np.random.randn(3) and compute the angle between them.
2. Verify that swapping the vectors gives the same angle (symmetry).
3. Find two vectors where cosine similarity is exactly 0. Can you come up with an example in 2D?

8. Projections and Decompositions

In this lab, we’ll learn how to split one vector into parts: one part that lies along another vector, and one part that is perpendicular. This process is called projection and decomposition. Projections let us measure “how much of a vector points in a given direction,” and decompositions give us a way to break vectors into useful components.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Projection formula The projection of vector \(v\) onto vector \(u\) is:

\[ \text{proj}_u(v) = \frac{v \cdot u}{u \cdot u} \, u \]

This gives the component of \(v\) that points in the direction of \(u\).

2. Computing projection in Python

v = np.array([3, 2])
u = np.array([2, 0])

proj_u_v = (np.dot(v, u) / np.dot(u, u)) * u
print("Projection of v onto u:", proj_u_v)

Projection of v onto u: [3. 0.]

Here, \(v = (3,2)\) and \(u = (2,0)\). The projection of v onto u is a vector pointing along the x-axis.

3. Decomposing into parallel and perpendicular parts

We can write:

\[ v = \text{proj}_u(v) + (v - \text{proj}_u(v)) \]

The first part is parallel to u, the second part is perpendicular.

perp = v - proj_u_v
print("Parallel part:", proj_u_v)
print("Perpendicular part:", perp)

Parallel part: [3. 0.]
Perpendicular part: [0. 2.]

4. Visualizing projection and decomposition

plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='v')
plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b', label='u')
plt.quiver(0, 0, proj_u_v[0], proj_u_v[1], angles='xy', scale_units='xy', scale=1, color='g', label='proj_u(v)')
plt.quiver(proj_u_v[0], proj_u_v[1], perp[0], perp[1], angles='xy', scale_units='xy', scale=1, color='m', label='perpendicular')

plt.xlim(-1, 5)
plt.ylim(-1, 4)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.show()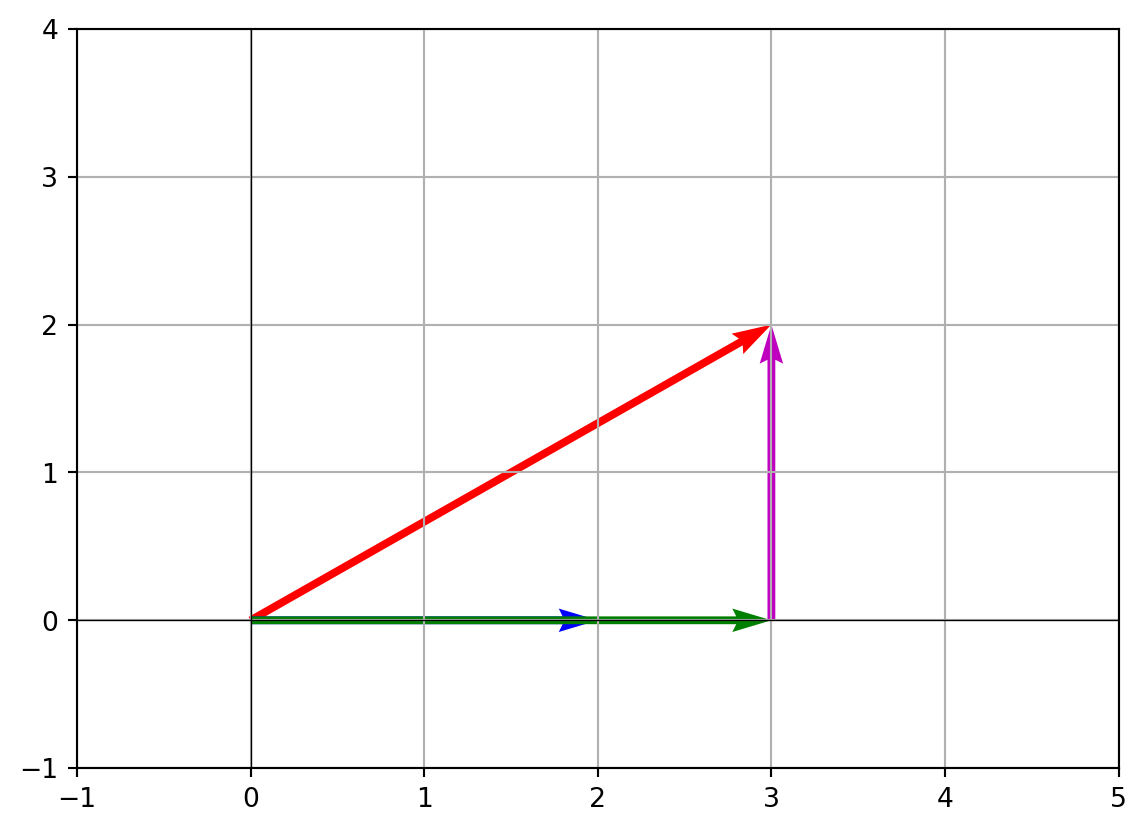

You’ll see v (red), u (blue), the projection (green), and the perpendicular remainder (magenta).

5. Projection in higher dimensions

This formula works in any dimension:

a = np.array([1,2,3])
b = np.array([0,1,0])

proj = (np.dot(a,b)/np.dot(b,b)) * b
perp = a - proj

print("Projection of a onto b:", proj)
print("Perpendicular component:", perp)

Projection of a onto b: [0. 2. 0.]
Perpendicular component: [1. 0. 3.]

Even in 3D or higher, projections are about splitting into “along” and “across.”

Try It Yourself

1. Try projecting (2,3) onto (0,5). Where does it land?
2. Take a 3D vector like (4,2,6) and project it onto (1,0,0). What does this give you?
3. Change the base vector u to something not aligned with the axes, like (1,1). Does the projection still work?

9. Cauchy–Schwarz and Triangle Inequalities

This lab introduces two fundamental inequalities in linear algebra. They may look abstract at first, but they provide guarantees that always hold true for vectors. We’ll explore them with small examples in Python to see why they matter.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Cauchy–Schwarz inequality

The inequality states:

\[ |v \cdot u| \leq \|v\| \, \|u\| \]

It means the dot product is never “bigger” than the product of the vector lengths. Equality happens only if the two vectors are pointing in exactly the same (or opposite) direction.

v = np.array([3, 4])
u = np.array([1, 2])

lhs = abs(np.dot(v, u))
rhs = np.linalg.norm(v) * np.linalg.norm(u)

print("Left-hand side (|v·u|):", lhs)
print("Right-hand side (‖v‖‖u‖):", rhs)
print("Inequality holds?", lhs <= rhs)

Left-hand side (|v·u|): 11
Right-hand side (‖v‖‖u‖): 11.180339887498949
Inequality holds? True

2. Testing Cauchy–Schwarz with different vectors

pairs = [
    (np.array([1,0]), np.array([0,1])),  # perpendicular
    (np.array([2,3]), np.array([4,6])),  # multiples
    (np.array([-1,2]), np.array([3,-6])) # opposite multiples
]

for v,u in pairs:
    lhs = abs(np.dot(v, u))
    rhs = np.linalg.norm(v) * np.linalg.norm(u)
    print(f"v={v}, u={u} -> |v·u|={lhs}, ‖v‖‖u‖={rhs}, holds={lhs<=rhs}")

v=[1 0], u=[0 1] -> |v·u|=0, ‖v‖‖u‖=1.0, holds=True
v=[2 3], u=[4 6] -> |v·u|=26, ‖v‖‖u‖=25.999999999999996, holds=False
v=[-1  2], u=[ 3 -6] -> |v·u|=15, ‖v‖‖u‖=15.000000000000002, holds=True

• Perpendicular vectors give |v·u| = 0, far less than the product of norms.
• Multiples give equality (lhs = rhs).

3. Triangle inequality

The triangle inequality states:

\[ \|v + u\| \leq \|v\| + \|u\| \]

Geometrically, the length of one side of a triangle can never be longer than the sum of the other two sides.

v = np.array([3, 4])
u = np.array([1, 2])

lhs = np.linalg.norm(v + u)
rhs = np.linalg.norm(v) + np.linalg.norm(u)

print("‖v+u‖ =", lhs)
print("‖v‖ + ‖u‖ =", rhs)
print("Inequality holds?", lhs <= rhs)

‖v+u‖ = 7.211102550927978
‖v‖ + ‖u‖ = 7.23606797749979
Inequality holds? True

4. Visual demonstration with a triangle

import matplotlib.pyplot as plt

origin = np.array([0,0])
points = np.array([origin, v, v+u, origin])

plt.plot(points[:,0], points[:,1], 'ro-')  # triangle outline
plt.text(v[0], v[1], 'v')
plt.text(v[0]+u[0], v[1]+u[1], 'v+u')
plt.text(u[0], u[1], 'u')

plt.grid()
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.axis('equal')
plt.show()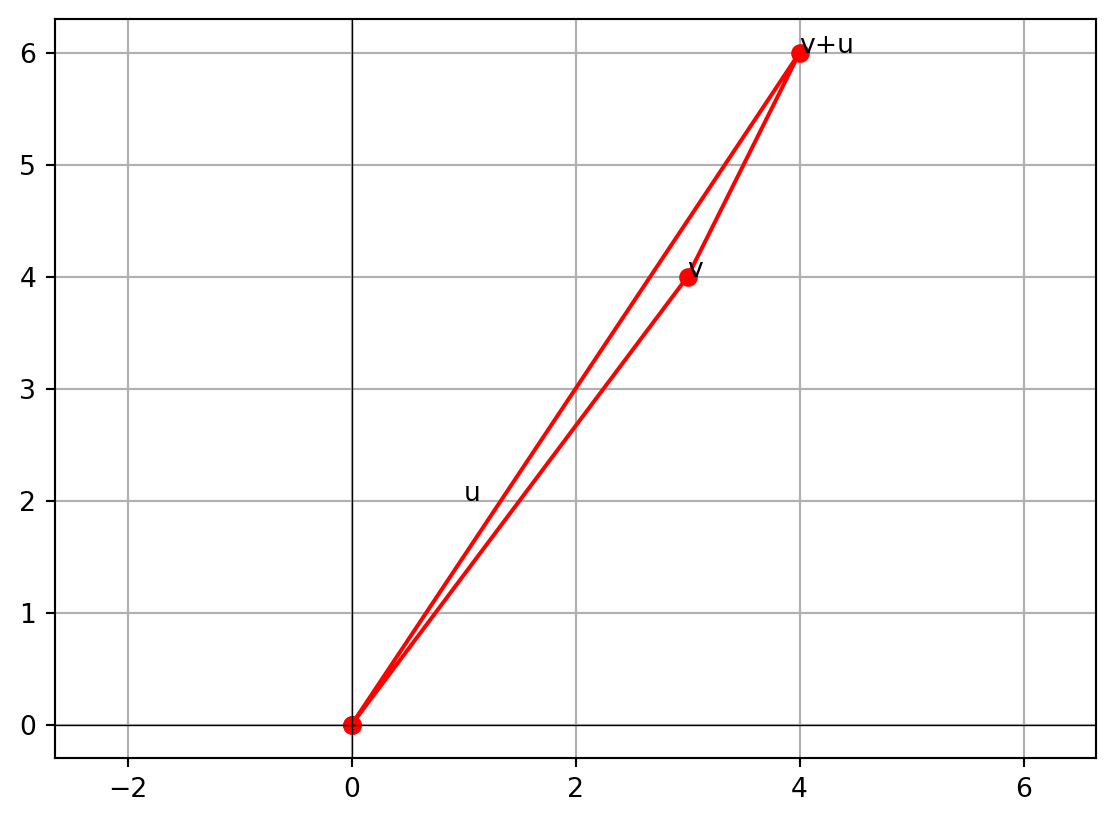

This triangle shows why the inequality is called the “triangle” inequality.

5. Testing triangle inequality with random vectors

for _ in range(5):
    v = np.random.randn(2)
    u = np.random.randn(2)
    lhs = np.linalg.norm(v+u)
    rhs = np.linalg.norm(v) + np.linalg.norm(u)
    print(f"‖v+u‖={lhs:.3f}, ‖v‖+‖u‖={rhs:.3f}, holds={lhs <= rhs}")

‖v+u‖=0.778, ‖v‖+‖u‖=2.112, holds=True
‖v+u‖=1.040, ‖v‖+‖u‖=2.621, holds=True
‖v+u‖=1.632, ‖v‖+‖u‖=2.482, holds=True
‖v+u‖=1.493, ‖v‖+‖u‖=2.250, holds=True
‖v+u‖=2.653, ‖v‖+‖u‖=2.692, holds=True

No matter what vectors you try, the inequality always holds.

The Takeaway

• Cauchy–Schwarz: The dot product is always bounded by the product of vector lengths.
• Triangle inequality: The length of one side of a triangle can’t exceed the sum of the other two.
• These inequalities form the backbone of geometry, analysis, and many proofs in linear algebra.

10. Orthonormal Sets in ℝ²/ℝ³

In this lab, we’ll explore orthonormal sets - collections of vectors that are both orthogonal (perpendicular) and normalized (length = 1). These sets are the “nicest” possible bases for vector spaces. In 2D and 3D, they correspond to the coordinate axes we already know, but we can also construct and test new ones.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Orthogonal vectors Two vectors are orthogonal if their dot product is zero.

x_axis = np.array([1, 0])
y_axis = np.array([0, 1])

print("x_axis · y_axis =", np.dot(x_axis, y_axis))  # should be 0

x_axis · y_axis = 0

So the standard axes are orthogonal.

2. Normalizing vectors Normalization means dividing a vector by its length to make its norm equal to 1.

v = np.array([3, 4])
v_normalized = v / np.linalg.norm(v)

print("Original v:", v)
print("Normalized v:", v_normalized)
print("Length of normalized v:", np.linalg.norm(v_normalized))

Original v: [3 4]
Normalized v: [0.6 0.8]
Length of normalized v: 1.0

Now v_normalized points in the same direction as v but has unit length.

3. Building an orthonormal set in 2D

u1 = np.array([1, 0])
u2 = np.array([0, 1])

print("u1 length:", np.linalg.norm(u1))
print("u2 length:", np.linalg.norm(u2))
print("u1 · u2 =", np.dot(u1,u2))

u1 length: 1.0
u2 length: 1.0
u1 · u2 = 0

Both have length 1, and their dot product is 0. That makes {u1, u2} an orthonormal set in 2D.

4. Visualizing 2D orthonormal vectors

plt.quiver(0,0,u1[0],u1[1],angles='xy',scale_units='xy',scale=1,color='r')
plt.quiver(0,0,u2[0],u2[1],angles='xy',scale_units='xy',scale=1,color='b')

plt.xlim(-1.5,1.5)
plt.ylim(-1.5,1.5)
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.show()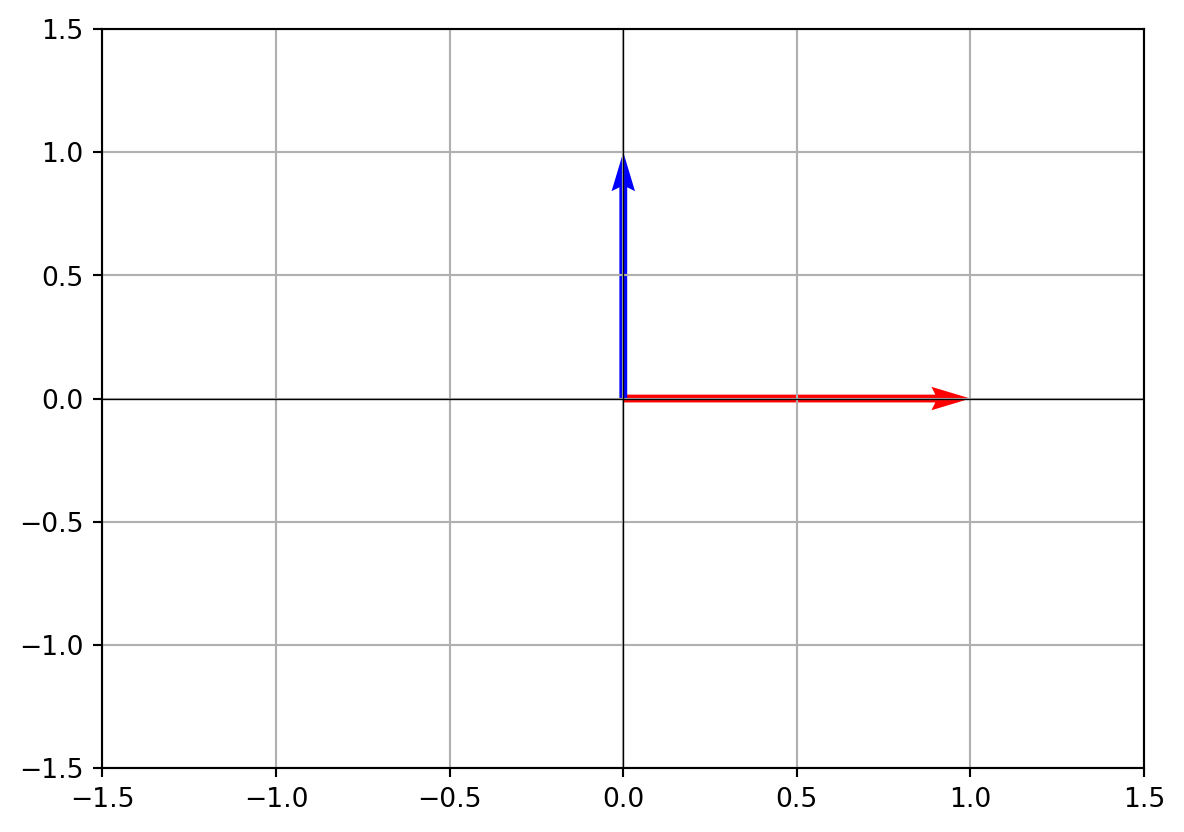

You’ll see the red and blue arrows at right angles, each of length 1.

5. Orthonormal set in 3D In 3D, the standard basis vectors are:

i = np.array([1,0,0])
j = np.array([0,1,0])
k = np.array([0,0,1])

print("‖i‖ =", np.linalg.norm(i))
print("‖j‖ =", np.linalg.norm(j))
print("‖k‖ =", np.linalg.norm(k))
print("i·j =", np.dot(i,j))
print("j·k =", np.dot(j,k))
print("i·k =", np.dot(i,k))

‖i‖ = 1.0
‖j‖ = 1.0
‖k‖ = 1.0
i·j = 0
j·k = 0
i·k = 0

Lengths are all 1, and dot products are 0. So {i, j, k} is an orthonormal set in ℝ³.

6. Testing if a set is orthonormal We can write a helper function:

def is_orthonormal(vectors):
    for i in range(len(vectors)):
        for j in range(len(vectors)):
            dot = np.dot(vectors[i], vectors[j])
            if i == j:
                if not np.isclose(dot, 1): return False
            else:
                if not np.isclose(dot, 0): return False
    return True

print(is_orthonormal([i, j, k]))  # True

True

7. Constructing a new orthonormal pair Not all orthonormal sets look like the axes.

u1 = np.array([1,1]) / np.sqrt(2)
u2 = np.array([-1,1]) / np.sqrt(2)

print("u1·u2 =", np.dot(u1,u2))
print("‖u1‖ =", np.linalg.norm(u1))
print("‖u2‖ =", np.linalg.norm(u2))

u1·u2 = 0.0
‖u1‖ = 0.9999999999999999
‖u2‖ = 0.9999999999999999

This gives a rotated orthonormal basis in 2D.

Try It Yourself

1. Normalize (2,2,1) to make it a unit vector.
2. Test whether the set {[1,0,0], [0,2,0], [0,0,3]} is orthonormal.
3. Construct two vectors in 2D that are not perpendicular. Normalize them and check if the dot product is still zero.

Chapter 2. Matrices and basic operations

11. Matrices as Tables and as Machines

Matrices can feel mysterious at first, but there are two simple ways to think about them:

1. As tables of numbers - just a grid you can store and manipulate.
2. As machines - something that takes a vector in and spits a new vector out.

In this lab, we’ll explore both views and see how they connect.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. A matrix as a table of numbers

A = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

print("Matrix A:\n", A)
print("Shape of A:", A.shape)

Matrix A:
 [[1 2 3]
 [4 5 6]]
Shape of A: (2, 3)

Here, A is a 2×3 matrix (2 rows, 3 columns).

• Rows = horizontal slices → [1,2,3] and [4,5,6]
• Columns = vertical slices → [1,4], [2,5], [3,6]

2. Accessing rows and columns

first_row = A[0]        # row 0
second_column = A[:,1]  # column 1

print("First row:", first_row)
print("Second column:", second_column)

First row: [1 2 3]
Second column: [2 5]

Rows are whole vectors too, and so are columns.

3. A matrix as a machine

A matrix can “act” on a vector. If x = [x1, x2, x3], then A·x is computed by taking linear combinations of the columns of A.

x = np.array([1, 0, -1])  # a 3D vector
result = A.dot(x)

print("A·x =", result)

A·x = [-2 -2]

Interpretation: multiply A by x = combine columns of A with weights from x.

\[ A \cdot x = 1 \cdot \text{(col 1)} + 0 \cdot \text{(col 2)} + (-1) \cdot \text{(col 3)} \]

4. Verifying column combination view

col1 = A[:,0]
col2 = A[:,1]
col3 = A[:,2]

manual = 1*col1 + 0*col2 + (-1)*col3
print("Manual combination:", manual)
print("A·x result:", result)

Manual combination: [-2 -2]
A·x result: [-2 -2]

They match exactly. This shows the “machine” interpretation is just a shortcut for column combinations.

5. Geometric intuition (2D example)

B = np.array([
    [2, 0],
    [0, 1]
])

v = np.array([1,2])
print("B·v =", B.dot(v))

B·v = [2 2]

Here, B scales the x-direction by 2 while leaving the y-direction alone. So (1,2) becomes (2,2).

Try It Yourself

1. Create a 3×3 identity matrix with np.eye(3) and multiply it by different vectors. What happens?
2. Build a matrix [[0,-1],[1,0]]. Try multiplying it by (1,0) and (0,1). What transformation is this?
3. Create your own 2×2 matrix that flips vectors across the x-axis. Test it on (1,2) and (−3,4).

The Takeaway

• A matrix is both a grid of numbers and a machine that transforms vectors.
• Matrix–vector multiplication is the same as combining columns with given weights.
• Thinking of matrices as machines helps build intuition for rotations, scalings, and other transformations later.

12. Matrix Shapes, Indexing, and Block Views

Matrices come in many shapes, and learning to read their structure is essential. Shape tells us how many rows and columns a matrix has. Indexing lets us grab specific entries, rows, or columns. Block views let us zoom in on submatrices, which is extremely useful for both theory and computation.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Matrix shapes

The shape of a matrix is (rows, columns).

A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

print("Matrix A:\n", A)
print("Shape of A:", A.shape)

Matrix A:
 [[1 2 3]
 [4 5 6]
 [7 8 9]]
Shape of A: (3, 3)

Here, A is a 3×3 matrix.

2. Indexing elements

In NumPy, rows and columns are 0-based. The first entry is A[0,0].

print("A[0,0] =", A[0,0])  # top-left element
print("A[1,2] =", A[1,2])  # second row, third column

A[0,0] = 1
A[1,2] = 6

3. Extracting rows and columns

row1 = A[0]       # first row
col2 = A[:,1]     # second column

print("First row:", row1)
print("Second column:", col2)

First row: [1 2 3]
Second column: [2 5 8]

Notice: A[i] gives a row, A[:,j] gives a column.

4. Slicing submatrices (block view)

You can slice multiple rows and columns to form a smaller matrix.

block = A[0:2, 1:3]  # rows 0–1, columns 1–2
print("Block submatrix:\n", block)

Block submatrix:
 [[2 3]
 [5 6]]

This block is:

\[ \begin{bmatrix} 2 & 3 \\ 5 & 6 \end{bmatrix} \]

5. Modifying parts of a matrix

A[0,0] = 99
print("Modified A:\n", A)

A[1,:] = [10, 11, 12]   # replace row 1
print("After replacing row 1:\n", A)

Modified A:
 [[99  2  3]
 [ 4  5  6]
 [ 7  8  9]]
After replacing row 1:
 [[99  2  3]
 [10 11 12]
 [ 7  8  9]]

6. Non-square matrices

Not all matrices are square. Shapes can be rectangular, too.

B = np.array([
    [1, 2],
    [3, 4],
    [5, 6]
])

print("Matrix B:\n", B)
print("Shape of B:", B.shape)

Matrix B:
 [[1 2]
 [3 4]
 [5 6]]
Shape of B: (3, 2)

Here, B is 3×2 (3 rows, 2 columns).

7. Block decomposition idea

We can think of large matrices as made of smaller blocks. This is common in linear algebra proofs and algorithms.

C = np.array([
    [1,2,3,4],
    [5,6,7,8],
    [9,10,11,12],
    [13,14,15,16]
])

top_left = C[0:2, 0:2]
bottom_right = C[2:4, 2:4]

print("Top-left block:\n", top_left)
print("Bottom-right block:\n", bottom_right)

Top-left block:
 [[1 2]
 [5 6]]
Bottom-right block:
 [[11 12]
 [15 16]]

This is the start of block matrix notation.

Try It Yourself

1. Create a 4×5 matrix with values 1–20 using np.arange(1,21).reshape(4,5). Find its shape.
2. Extract the middle row and last column.
3. Cut it into four 2×2 blocks. Can you reassemble them in a different order?

13. Matrix Addition and Scalar Multiplication

Now that we understand matrix shapes and indexing, let’s practice two of the simplest but most important operations: adding matrices and scaling them with numbers (scalars). These operations extend the rules we already know for vectors.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Adding two matrices You can add two matrices if (and only if) they have the same shape. Addition happens entry by entry.

A = np.array([
    [1, 2],
    [3, 4]
])

B = np.array([
    [5, 6],
    [7, 8]
])

C = A + B
print("A + B =\n", C)

A + B =
 [[ 6  8]
 [10 12]]

Each element in C is the sum of corresponding elements in A and B.

2. Scalar multiplication Multiplying a matrix by a scalar multiplies every entry by that number.

k = 3
D = k * A
print("3 * A =\n", D)

3 * A =
 [[ 3  6]
 [ 9 12]]

Here, each element of A is tripled.

3. Combining both operations We can mix addition and scaling, just like with vectors.

combo = 2*A - B
print("2A - B =\n", combo)

2A - B =
 [[-3 -2]
 [-1  0]]

This creates new matrices as linear combinations of others.

4. Zero matrix A matrix of all zeros acts like “nothing happens” for addition.

zero = np.zeros((2,2))
print("Zero matrix:\n", zero)
print("A + Zero =\n", A + zero)

Zero matrix:
 [[0. 0.]
 [0. 0.]]
A + Zero =
 [[1. 2.]
 [3. 4.]]

5. Shape mismatch (what fails) If shapes don’t match, NumPy throws an error.

X = np.array([
    [1,2,3],
    [4,5,6]
])

try:
    print(A + X)
except ValueError as e:
    print("Error:", e)

Error: operands could not be broadcast together with shapes (2,2) (2,3) 

This shows why shape consistency matters.

Try It Yourself

1. Create two random 3×3 matrices with np.random.randint(0,10,(3,3)) and add them.
2. Multiply a 4×4 matrix by -1. What happens to its entries?
3. Compute 3A + 2B with the matrices from above. Compare with doing each step manually.

14. Matrix–Vector Product (Linear Combinations of Columns)

This lab introduces the matrix–vector product, one of the most important operations in linear algebra. Multiplying a matrix by a vector doesn’t just crunch numbers - it produces a new vector by combining the matrix’s columns in a weighted way.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. A simple matrix and vector

A = np.array([
    [1, 2],
    [3, 4],
    [5, 6]
])  # 3×2 matrix

x = np.array([2, -1])  # 2D vector

Here, A has 2 columns, so we can multiply it by a 2D vector x.

2. Matrix–vector multiplication in NumPy

y = A.dot(x)
print("A·x =", y)

A·x = [0 2 4]

Result: a 3D vector.

3. Interpreting the result as linear combinations

Matrix A has two columns:

col1 = A[:,0]   # first column
col2 = A[:,1]   # second column

manual = 2*col1 + (-1)*col2
print("Manual linear combination:", manual)

Manual linear combination: [0 2 4]

This matches A·x. In words: multiply each column by the corresponding entry of x and then add them up.

4. Another example (geometry)

B = np.array([
    [2, 0],
    [0, 1]
])  # stretches x-axis by 2

v = np.array([1, 3])
print("B·v =", B.dot(v))

B·v = [2 3]

Here, (1,3) becomes (2,3). The x-component was doubled, while y stayed the same.

5. Visualization of matrix action

import matplotlib.pyplot as plt

# draw original vector
plt.quiver(0,0,v[0],v[1],angles='xy',scale_units='xy',scale=1,color='r',label='v')

# draw transformed vector
v_transformed = B.dot(v)
plt.quiver(0,0,v_transformed[0],v_transformed[1],angles='xy',scale_units='xy',scale=1,color='b',label='B·v')

plt.xlim(-1,4)
plt.ylim(-1,4)
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.show()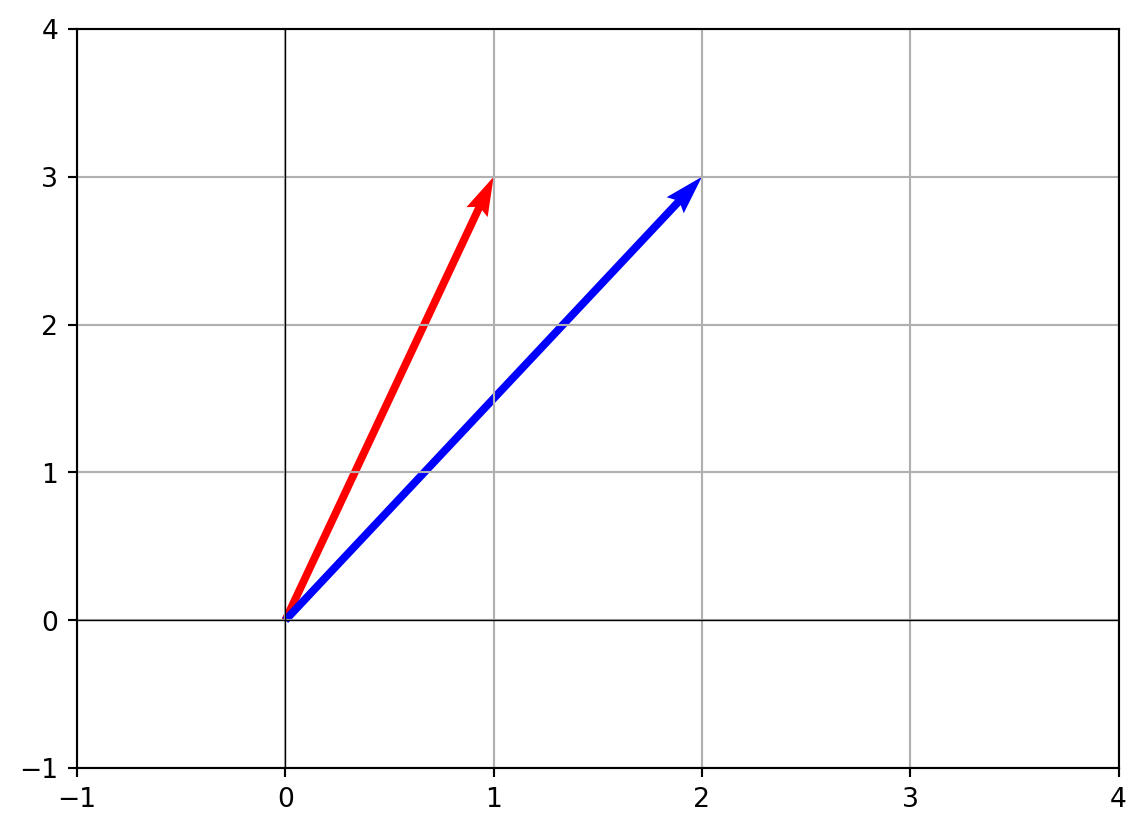

Red arrow = original vector, blue arrow = transformed vector.

Try It Yourself

1. Multiply

   \[ A = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ -1 & 2\end{bmatrix},\; x = [3,1] \]

   What’s the result?

2. Replace B with [[0,-1],[1,0]]. Multiply it by (1,0) and (0,1). What geometric transformation does this represent?

3. For a 4×4 identity matrix (np.eye(4)), try multiplying by any 4D vector. What do you observe?

15. Matrix–Matrix Product (Composition of Linear Steps)

Matrix–matrix multiplication is how we combine two linear transformations into one. Instead of applying one transformation, then another, we can multiply their matrices and get a single matrix that does both at once.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Matrix–matrix multiplication in NumPy

A = np.array([
    [1, 2],
    [3, 4]
])  # 2×2

B = np.array([
    [2, 0],
    [1, 2]
])  # 2×2

C = A.dot(B)   # or A @ B
print("A·B =\n", C)

A·B =
 [[ 4  4]
 [10  8]]

The result C is another 2×2 matrix.

2. Manual computation

Each entry of C is computed as a row of A dotted with a column of B:

c11 = A[0,:].dot(B[:,0])
c12 = A[0,:].dot(B[:,1])
c21 = A[1,:].dot(B[:,0])
c22 = A[1,:].dot(B[:,1])

print("Manual C =\n", np.array([[c11,c12],[c21,c22]]))

Manual C =
 [[ 4  4]
 [10  8]]

This should match A·B.

3. Geometric interpretation

Let’s see how two transformations combine.

• Matrix B scales x by 2 and stretches y by 2.
• Matrix A applies another linear transformation.

Together, C = A·B does both in one step.

v = np.array([1,1])

print("First apply B:", B.dot(v))
print("Then apply A:", A.dot(B.dot(v)))
print("Directly with C:", C.dot(v))

First apply B: [2 3]
Then apply A: [ 8 18]
Directly with C: [ 8 18]

The result is the same: applying B then A is equivalent to applying C.

4. Non-square matrices

Matrix multiplication also works for rectangular matrices, as long as the inner dimensions match.

M = np.array([
    [1, 0, 2],
    [0, 1, 3]
])  # 2×3

N = np.array([
    [1, 2],
    [0, 1],
    [4, 0]
])  # 3×2

P = M.dot(N)  # result is 2×2
print("M·N =\n", P)

M·N =
 [[ 9  2]
 [12  1]]

Shape rule: (2×3)·(3×2) = (2×2).

5. Associativity (but not commutativity)

Matrix multiplication is associative: (A·B)·C = A·(B·C). But it’s not commutative: in general, A·B ≠ B·A.

A = np.array([[1,2],[3,4]])
B = np.array([[0,1],[1,0]])

print("A·B =\n", A.dot(B))
print("B·A =\n", B.dot(A))

A·B =
 [[2 1]
 [4 3]]
B·A =
 [[3 4]
 [1 2]]

The two results are different.

Try It Yourself

1. Multiply

   \[ A = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix},\; B = \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix} \]

   What transformation does A·B represent?

2. Create a random 3×2 matrix and a 2×4 matrix. Multiply them. What shape is the result?

3. Verify with Python that (A·B)·C = A·(B·C) for some 3×3 random matrices.

16. Identity, Inverse, and Transpose

In this lab, we’ll meet three special matrix operations and objects: the identity matrix, the inverse, and the transpose. These are the building blocks of matrix algebra, each with a simple meaning but deep importance.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Identity matrix The identity matrix is like the number 1 for matrices: multiplying by it changes nothing.

I = np.eye(3)  # 3×3 identity matrix
print("Identity matrix:\n", I)

A = np.array([
    [2, 1, 0],
    [0, 1, 3],
    [4, 0, 1]
])

print("A·I =\n", A.dot(I))
print("I·A =\n", I.dot(A))

Identity matrix:
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
A·I =
 [[2. 1. 0.]
 [0. 1. 3.]
 [4. 0. 1.]]
I·A =
 [[2. 1. 0.]
 [0. 1. 3.]
 [4. 0. 1.]]

Both equal A.

2. Transpose The transpose flips rows and columns.

B = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

print("B:\n", B)
print("B.T:\n", B.T)

B:
 [[1 2 3]
 [4 5 6]]
B.T:
 [[1 4]
 [2 5]
 [3 6]]

• Original: 2×3
• Transpose: 3×2

Geometrically, transpose swaps the axes when vectors are viewed in row/column form.

3. Inverse The inverse matrix is like dividing by a number: multiplying a matrix by its inverse gives the identity.

C = np.array([
    [2, 1],
    [5, 3]
])

C_inv = np.linalg.inv(C)
print("Inverse of C:\n", C_inv)

print("C·C_inv =\n", C.dot(C_inv))
print("C_inv·C =\n", C_inv.dot(C))

Inverse of C:
 [[ 3. -1.]
 [-5.  2.]]
C·C_inv =
 [[ 1.00000000e+00  2.22044605e-16]
 [-8.88178420e-16  1.00000000e+00]]
C_inv·C =
 [[1.00000000e+00 3.33066907e-16]
 [0.00000000e+00 1.00000000e+00]]

Both products are (approximately) the identity.

4. Matrices that don’t have inverses Not every matrix is invertible. If a matrix is singular (determinant = 0), it has no inverse.

D = np.array([
    [1, 2],
    [2, 4]
])

try:
    np.linalg.inv(D)
except np.linalg.LinAlgError as e:
    print("Error:", e)

Error: Singular matrix

Here, the second row is a multiple of the first, so D can’t be inverted.

5. Transpose and inverse together For invertible matrices,

\[ (A^T)^{-1} = (A^{-1})^T \]

We can check this numerically:

A = np.array([
    [1, 2],
    [3, 5]
])

lhs = np.linalg.inv(A.T)
rhs = np.linalg.inv(A).T

print("Do they match?", np.allclose(lhs, rhs))

Do they match? True

Try It Yourself

1. Create a 4×4 identity matrix. Multiply it by any 4×1 vector. Does it change?
2. Take a random 2×2 matrix with np.random.randint. Compute its inverse and check if multiplying gives identity.
3. Pick a rectangular 3×2 matrix. What happens when you try np.linalg.inv? Why?
4. Compute (A.T).T for some matrix A. What do you notice?

17. Symmetric, Diagonal, Triangular, and Permutation Matrices

In this lab, we’ll meet four important families of special matrices. They have patterns that make them easier to understand, compute with, and use in algorithms.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Symmetric matrices A matrix is symmetric if it equals its transpose: \(A = A^T\).

A = np.array([
    [2, 3, 4],
    [3, 5, 6],
    [4, 6, 8]
])

print("A:\n", A)
print("A.T:\n", A.T)
print("Is symmetric?", np.allclose(A, A.T))

A:
 [[2 3 4]
 [3 5 6]
 [4 6 8]]
A.T:
 [[2 3 4]
 [3 5 6]
 [4 6 8]]
Is symmetric? True

Symmetric matrices appear in physics, optimization, and statistics (e.g., covariance matrices).

2. Diagonal matrices A diagonal matrix has nonzero entries only on the main diagonal.

D = np.diag([1, 5, 9])
print("Diagonal matrix:\n", D)

x = np.array([2, 3, 4])
print("D·x =", D.dot(x))  # scales each component

Diagonal matrix:
 [[1 0 0]
 [0 5 0]
 [0 0 9]]
D·x = [ 2 15 36]

Diagonal multiplication simply scales each coordinate separately.

3. Triangular matrices Upper triangular: all entries below the diagonal are zero. Lower triangular: all entries above the diagonal are zero.

U = np.array([
    [1, 2, 3],
    [0, 4, 5],
    [0, 0, 6]
])

L = np.array([
    [7, 0, 0],
    [8, 9, 0],
    [1, 2, 3]
])

print("Upper triangular U:\n", U)
print("Lower triangular L:\n", L)

Upper triangular U:
 [[1 2 3]
 [0 4 5]
 [0 0 6]]
Lower triangular L:
 [[7 0 0]
 [8 9 0]
 [1 2 3]]

These are important in solving linear systems (e.g., Gaussian elimination).

4. Permutation matrices A permutation matrix rearranges the order of coordinates. Each row and each column has exactly one 1, everything else is 0.

P = np.array([
    [0, 1, 0],
    [0, 0, 1],
    [1, 0, 0]
])

print("Permutation matrix P:\n", P)

v = np.array([10, 20, 30])
print("P·v =", P.dot(v))

Permutation matrix P:
 [[0 1 0]
 [0 0 1]
 [1 0 0]]
P·v = [20 30 10]

Here, P cycles (10,20,30) into (20,30,10).

5. Checking properties

def is_symmetric(M): return np.allclose(M, M.T)
def is_diagonal(M): return np.count_nonzero(M - np.diag(np.diag(M))) == 0
def is_upper_triangular(M): return np.allclose(M, np.triu(M))
def is_lower_triangular(M): return np.allclose(M, np.tril(M))

print("A symmetric?", is_symmetric(A))
print("D diagonal?", is_diagonal(D))
print("U upper triangular?", is_upper_triangular(U))
print("L lower triangular?", is_lower_triangular(L))

A symmetric? True
D diagonal? True
U upper triangular? True
L lower triangular? True

Try It Yourself

1. Create a random symmetric matrix by generating any matrix M and computing (M + M.T)/2.
2. Build a 4×4 diagonal matrix with diagonal entries [2,4,6,8] and multiply it by [1,1,1,1].
3. Make a permutation matrix that swaps the first and last components of a 3D vector.
4. Check whether the identity matrix is diagonal, symmetric, upper triangular, and lower triangular all at once.

18. Trace and Basic Matrix Properties

In this lab, we’ll introduce the trace of a matrix and a few quick properties that often appear in proofs, algorithms, and applications. The trace is simple to compute but surprisingly powerful.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. What is the trace? The trace of a square matrix is the sum of its diagonal entries:

\[ \text{tr}(A) = \sum_i A_{ii} \]

A = np.array([
    [2, 1, 3],
    [0, 4, 5],
    [7, 8, 6]
])

trace_A = np.trace(A)
print("Matrix A:\n", A)
print("Trace of A =", trace_A)

Matrix A:
 [[2 1 3]
 [0 4 5]
 [7 8 6]]
Trace of A = 12

Here, trace = \(2 + 4 + 6 = 12\).

2. Trace is linear For matrices A and B:

\[ \text{tr}(A+B) = \text{tr}(A) + \text{tr}(B) \]

\[ \text{tr}(cA) = c \cdot \text{tr}(A) \]

B = np.array([
    [1, 0, 0],
    [0, 2, 0],
    [0, 0, 3]
])

print("tr(A+B) =", np.trace(A+B))
print("tr(A) + tr(B) =", np.trace(A) + np.trace(B))

print("tr(3A) =", np.trace(3*A))
print("3 * tr(A) =", 3*np.trace(A))

tr(A+B) = 18
tr(A) + tr(B) = 18
tr(3A) = 36
3 * tr(A) = 36

3. Trace of a product One important property is:

\[ \text{tr}(AB) = \text{tr}(BA) \]

C = np.array([
    [0,1],
    [2,3]
])

D = np.array([
    [4,5],
    [6,7]
])

print("tr(CD) =", np.trace(C.dot(D)))
print("tr(DC) =", np.trace(D.dot(C)))

tr(CD) = 37
tr(DC) = 37

Both are equal, even though CD and DC are different matrices.

4. Trace and eigenvalues The trace equals the sum of eigenvalues of a matrix (counting multiplicities).

vals, vecs = np.linalg.eig(A)
print("Eigenvalues:", vals)
print("Sum of eigenvalues =", np.sum(vals))
print("Trace =", np.trace(A))

Eigenvalues: [12.83286783  2.13019807 -2.9630659 ]
Sum of eigenvalues = 12.000000000000007
Trace = 12

The results should match (within rounding error).

5. Quick invariants

• Trace doesn’t change under transpose: tr(A) = tr(A.T)
• Trace doesn’t change under similarity transforms: tr(P^-1 A P) = tr(A)

print("tr(A) =", np.trace(A))
print("tr(A.T) =", np.trace(A.T))

tr(A) = 12
tr(A.T) = 12

Try It Yourself

1. Create a 2×2 rotation matrix for 90°:

   \[ R = \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix} \]

   What is its trace? What does that tell you about its eigenvalues?

2. Make a random 3×3 matrix and compare tr(A) with the sum of eigenvalues.

3. Test tr(AB) and tr(BA) with a rectangular matrix A (e.g. 2×3) and B (3×2). Do they still match?

19. Affine Transforms and Homogeneous Coordinates

Affine transformations let us do more than just linear operations - they include translations (shifting points), which ordinary matrices can’t handle alone. To unify rotations, scalings, reflections, and translations, we use homogeneous coordinates.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Linear transformations vs affine transformations

• A linear transformation can rotate, scale, or shear, but always keeps the origin fixed.
• An affine transformation allows translation as well.

For example, shifting every point by (2,3) is affine but not linear.

2. Homogeneous coordinates idea We add an extra coordinate (usually 1) to vectors.

• A 2D point (x,y) becomes (x,y,1).
• A 3D point (x,y,z) becomes (x,y,z,1).

This trick lets us represent translations using matrix multiplication.

3. 2D translation matrix

\[ T = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \]

T = np.array([
    [1, 0, 2],
    [0, 1, 3],
    [0, 0, 1]
])

p = np.array([1, 1, 1])  # point at (1,1)
p_translated = T.dot(p)

print("Original point:", p)
print("Translated point:", p_translated)

Original point: [1 1 1]
Translated point: [3 4 1]

This shifts (1,1) to (3,4).

4. Combining rotation and translation

A 90° rotation around the origin in 2D:

R = np.array([
    [0, -1, 0],
    [1,  0, 0],
    [0,  0, 1]
])

M = T.dot(R)  # rotate then translate
print("Combined transform:\n", M)

p = np.array([1, 0, 1])
print("Rotated + translated point:", M.dot(p))

Combined transform:
 [[ 0 -1  2]
 [ 1  0  3]
 [ 0  0  1]]
Rotated + translated point: [2 4 1]

Now we can apply rotation and translation in one step.

5. Visualization of translation

points = np.array([
    [0,0,1],
    [1,0,1],
    [1,1,1],
    [0,1,1]
])  # a unit square

transformed = points.dot(T.T)

plt.scatter(points[:,0], points[:,1], color='r', label='original')
plt.scatter(transformed[:,0], transformed[:,1], color='b', label='translated')

for i in range(len(points)):
    plt.arrow(points[i,0], points[i,1],
              transformed[i,0]-points[i,0],
              transformed[i,1]-points[i,1],
              head_width=0.05, color='gray')

plt.legend()
plt.axis('equal')
plt.grid()
plt.show()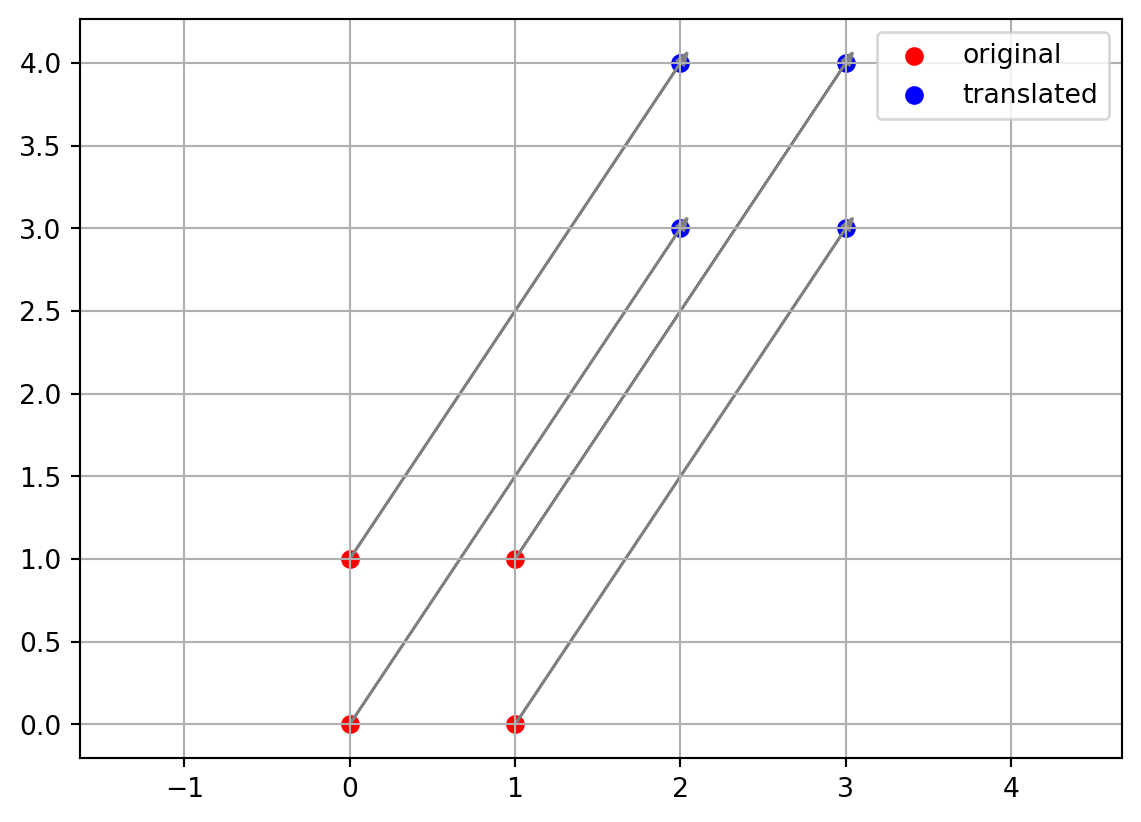

You’ll see the red unit square moved to a blue unit square shifted by (2,3).

6. Extending to 3D In 3D, homogeneous coordinates use 4×4 matrices. Translations, rotations, and scalings all fit the same framework.

T3 = np.array([
    [1,0,0,5],
    [0,1,0,-2],
    [0,0,1,3],
    [0,0,0,1]
])

p3 = np.array([1,2,3,1])
print("Translated 3D point:", T3.dot(p3))

Translated 3D point: [6 0 6 1]

This shifts (1,2,3) to (6,0,6).

Try It Yourself

1. Build a scaling matrix in homogeneous coordinates that doubles both x and y, and apply it to (1,1).
2. Create a 2D transform that rotates by 90° and then shifts by (−2,1). Apply it to (0,2).
3. In 3D, translate (0,0,0) by (10,10,10). What homogeneous matrix did you use?

20. Computing with Matrices (Cost Counts and Simple Speedups)

Working with matrices is not just about theory - in practice, we care about how much computation it takes to perform operations, and how we can make them faster. This lab introduces basic cost analysis (counting operations) and demonstrates simple NumPy optimizations.

Set Up Your Lab

import numpy as np
import time

Step-by-Step Code Walkthrough

1. Counting operations (matrix–vector multiply)

If A is an \(m \times n\) matrix and x is an \(n\)-dimensional vector, computing A·x takes about \(m \times n\) multiplications and the same number of additions.

m, n = 3, 4
A = np.random.randint(1,10,(m,n))
x = np.random.randint(1,10,n)

print("Matrix A:\n", A)
print("Vector x:", x)
print("A·x =", A.dot(x))

Matrix A:
 [[6 6 6 2]
 [1 1 1 1]
 [1 8 7 4]]
Vector x: [6 5 4 5]
A·x = [100  20  94]

Here the cost is \(3 \times 4 = 12\) multiplications + 12 additions.

2. Counting operations (matrix–matrix multiply)

For an \(m \times n\) times \(n \times p\) multiplication, the cost is about \(m \times n \times p\).

m, n, p = 3, 4, 2
A = np.random.randint(1,10,(m,n))
B = np.random.randint(1,10,(n,p))

C = A.dot(B)
print("A·B =\n", C)

A·B =
 [[ 59  92]
 [ 43  81]
 [ 65 102]]

Here the cost is \(3 \times 4 \times 2 = 24\) multiplications + 24 additions.

3. Timing with NumPy (vectorized vs loop)

NumPy is optimized in C and Fortran under the hood. Let’s compare matrix multiplication with and without vectorization.

n = 50
A = np.random.randn(n,n)
B = np.random.randn(n,n)

# Vectorized
start = time.time()
C1 = A.dot(B)
end = time.time()
print("Vectorized dot:", round(end-start,3), "seconds")

# Manual loops
C2 = np.zeros((n,n))
start = time.time()
for i in range(n):
    for j in range(n):
        for k in range(n):
            C2[i,j] += A[i,k]*B[k,j]
end = time.time()
print("Triple loop:", round(end-start,3), "seconds")

Vectorized dot: 0.0 seconds
Triple loop: 0.026 seconds

The vectorized version should be thousands of times faster.

4. Broadcasting tricks

NumPy lets us avoid loops by broadcasting operations across entire rows or columns.

A = np.array([
    [1,2,3],
    [4,5,6]
])

# Add 10 to every entry
print("A+10 =\n", A+10)

# Multiply each row by a different scalar
scales = np.array([1,10])[:,None]
print("Row-scaled A =\n", A*scales)

A+10 =
 [[11 12 13]
 [14 15 16]]
Row-scaled A =
 [[ 1  2  3]
 [40 50 60]]

5. Memory and data types

For large computations, data type matters.

A = np.random.randn(1000,1000).astype(np.float32)  # 32-bit floats
B = np.random.randn(1000,1000).astype(np.float32)

start = time.time()
C = A.dot(B)
print("Result shape:", C.shape, "dtype:", C.dtype)
print("Time:", round(time.time()-start,3), "seconds")

Result shape: (1000, 1000) dtype: float32
Time: 0.002 seconds

Using float32 instead of float64 halves memory use and can speed up computation (at the cost of some precision).

Try It Yourself

1. Compute the cost of multiplying a 200×500 matrix with a 500×1000 matrix. How many multiplications are needed?
2. Time matrix multiplication for sizes 100, 500, 1000 in NumPy. How does the time scale?
3. Experiment with float32 vs float64 in NumPy. How do speed and memory change?
4. Try broadcasting: multiply each column of a matrix by [1,2,3,...].

The Takeaway

• Matrix operations have predictable computational costs: A·x ~ \(m \times n\), A·B ~ \(m \times n \times p\).
• Vectorized NumPy operations are vastly faster than Python loops.
• Broadcasting and choosing the right data type are simple speedups every beginner should learn.

Chapter 3. Linear Systems and Elimination

21. From Equations to Matrices (Augmenting and Encoding)

Linear algebra often begins with solving systems of linear equations. For example:

\[ \begin{cases} x + 2y = 5 \\ 3x - y = 4 \end{cases} \]

Instead of juggling symbols, we can encode the entire system into a matrix. This is the key idea that lets computers handle thousands or millions of equations efficiently.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Write a system of equations

We’ll use this small example:

\[ \begin{cases} 2x + y = 8 \\ -3x + 4y = -11 \end{cases} \]

2. Encode coefficients and constants

• Coefficient matrix \(A\): numbers multiplying variables.
• Variable vector \(x\): unknowns [x, y].
• Constant vector \(b\): right-hand side.

A = np.array([
    [2, 1],
    [-3, 4]
])

b = np.array([8, -11])

print("Coefficient matrix A:\n", A)
print("Constants vector b:", b)

Coefficient matrix A:
 [[ 2  1]
 [-3  4]]
Constants vector b: [  8 -11]

So the system is \(A·x = b\).

3. Augmented matrix

We can bundle the system into one compact matrix:

\[ [A|b] = \begin{bmatrix}2 & 1 & | & 8 \\ -3 & 4 & | & -11 \end{bmatrix} \]

augmented = np.column_stack((A, b))
print("Augmented matrix:\n", augmented)

Augmented matrix:
 [[  2   1   8]
 [ -3   4 -11]]

This format is useful for elimination algorithms.

4. Solving directly with NumPy

solution = np.linalg.solve(A, b)
print("Solution (x,y):", solution)

Solution (x,y): [3.90909091 0.18181818]

Here NumPy solves the system using efficient algorithms.

5. Checking the solution

Always verify:

check = A.dot(solution)
print("A·x =", check, "should equal b =", b)

A·x = [  8. -11.] should equal b = [  8 -11]

6. Another example (3 variables)

\[ \begin{cases} x + y + z = 6 \\ 2x - y + z = 3 \\ - x + 2y - z = 2 \end{cases} \]

A = np.array([
    [1, 1, 1],
    [2, -1, 1],
    [-1, 2, -1]
])

b = np.array([6, 3, 2])

print("Augmented matrix:\n", np.column_stack((A, b)))
print("Solution:", np.linalg.solve(A, b))

Augmented matrix:
 [[ 1  1  1  6]
 [ 2 -1  1  3]
 [-1  2 -1  2]]
Solution: [2.33333333 2.66666667 1.        ]

Try It Yourself

1. Encode the system:

   \[ \begin{cases} 2x - y = 1 \\ x + 3y = 7 \end{cases} \]

   Write A and b, then solve.

2. For a 3×3 system, try creating a random coefficient matrix with np.random.randint(-5,5,(3,3)) and a random b. Use np.linalg.solve.

3. Modify the constants b slightly and see how the solution changes. This introduces the idea of sensitivity.

The Takeaway

• Systems of linear equations can be neatly written as \(A·x = b\).
• The augmented matrix \([A|b]\) is a compact way to set up elimination.
• This matrix encoding transforms algebra problems into matrix problems - the gateway to all of linear algebra.

22. Row Operations (Legal Moves That Keep Solutions)

When solving linear systems, we don’t want to change the solutions - just simplify the system into an easier form. This is where row operations come in. They are the “legal moves” we can do on an augmented matrix \([A|b]\) without changing the solution set.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Three legal row operations

2. Swap two rows \((R_i \leftrightarrow R_j)\)

3. Multiply a row by a nonzero scalar \((R_i \to c·R_i)\)

4. Replace a row with itself plus a multiple of another row \((R_i \to R_i + c·R_j)\)

These preserve the solution set.

2. Start with an augmented matrix

System:

\[ \begin{cases} x + 2y = 5 \\ 3x + 4y = 6 \end{cases} \]

A = np.array([
    [1, 2, 5],
    [3, 4, 6]
], dtype=float)

print("Initial augmented matrix:\n", A)

Initial augmented matrix:
 [[1. 2. 5.]
 [3. 4. 6.]]

3. Row swap

Swap row 0 and row 1.

A[[0,1]] = A[[1,0]]
print("After swapping rows:\n", A)

After swapping rows:
 [[3. 4. 6.]
 [1. 2. 5.]]

4. Multiply a row by a scalar

Make the pivot in row 0 equal to 1.

A[0] = A[0] / A[0,0]
print("After scaling first row:\n", A)

After scaling first row:
 [[1.         1.33333333 2.        ]
 [1.         2.         5.        ]]

5. Add a multiple of another row

Eliminate the first column of row 1.

A[1] = A[1] - 3*A[0]
print("After eliminating x from second row:\n", A)

After eliminating x from second row:
 [[ 1.          1.33333333  2.        ]
 [-2.         -2.         -1.        ]]

Now the system is simpler: second row has only y.

6. Solving from the new system

y = A[1,2] / A[1,1]
x = (A[0,2] - A[0,1]*y) / A[0,0]
print("Solution: x =", x, ", y =", y)

Solution: x = 1.3333333333333335 , y = 0.5

7. Using NumPy step-by-step vs solver

coeff = np.array([[1,2],[3,4]])
const = np.array([5,6])
print("np.linalg.solve result:", np.linalg.solve(coeff,const))

np.linalg.solve result: [-4.   4.5]

Both methods give the same solution.

Try It Yourself

1. Take the system:

   \[ \begin{cases} 2x + y = 7 \\ x - y = 1 \end{cases} \]

   Write its augmented matrix, then:

   • Swap rows.
   • Scale the first row.
   • Eliminate one variable.

2. Create a random 3×3 system with integers between -5 and 5. Perform at least one of each row operation manually in code.

3. Experiment with multiplying a row by 0. What happens, and why is this not allowed as a legal operation?

The Takeaway

• The three legal row operations are row swap, row scaling, and row replacement.
• These steps preserve the solution set while moving toward a simpler form.
• They are the foundation of Gaussian elimination, the standard algorithm for solving linear systems.

23. Row-Echelon and Reduced Row-Echelon Forms (Target Shapes)

When solving systems, our goal is to simplify the augmented matrix into a standard shape where the solutions are easy to read. These shapes are called row-echelon form (REF) and reduced row-echelon form (RREF).

Set Up Your Lab

import numpy as np
from sympy import Matrix

We’ll use NumPy for basic work and SymPy for exact RREF (since NumPy doesn’t have it built-in).

Step-by-Step Code Walkthrough

1. Row-Echelon Form (REF)

• All nonzero rows are above any zero rows.
• Each leading entry (pivot) is to the right of the pivot in the row above.
• Pivots are usually scaled to 1, but not strictly required.

Example system:

\[ \begin{cases} x + 2y + z = 7 \\ 2x + 4y + z = 12 \\ 3x + 6y + 2z = 17 \end{cases} \]

A = np.array([
    [1, 2, 1, 7],
    [2, 4, 1, 12],
    [3, 6, 2, 17]
], dtype=float)

print("Augmented matrix:\n", A)

Augmented matrix:
 [[ 1.  2.  1.  7.]
 [ 2.  4.  1. 12.]
 [ 3.  6.  2. 17.]]

Perform elimination manually:

# eliminate first column entries below pivot
A[1] = A[1] - 2*A[0]
A[2] = A[2] - 3*A[0]
print("After eliminating first column:\n", A)

After eliminating first column:
 [[ 1.  2.  1.  7.]
 [ 0.  0. -1. -2.]
 [ 0.  0. -1. -4.]]

Now the pivots move diagonally across the matrix - this is row-echelon form.

2. Reduced Row-Echelon Form (RREF) In RREF, we go further:

• Every pivot = 1.
• Every pivot is the only nonzero in its column.

Instead of coding manually, we’ll let SymPy handle it:

M = Matrix([
    [1, 2, 1, 7],
    [2, 4, 1, 12],
    [3, 6, 2, 17]
])

M_rref = M.rref()
print("RREF form:\n", M_rref[0])

RREF form:
 Matrix([[1, 2, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])

SymPy shows the final canonical form.

3. Reading solutions from RREF

If the RREF looks like:

\[ \begin{bmatrix} 1 & 0 & a & b \\ 0 & 1 & c & d \\ 0 & 0 & 0 & 0 \end{bmatrix} \]

It means:

• The first two variables are leading (pivots).
• The third variable is free.
• Solutions can be written in terms of the free variable.

4. A quick example with free variables

System:

\[ x + y + z = 3 \\ 2x + y - z = 0 \]

M2 = Matrix([
    [1,1,1,3],
    [2,1,-1,0]
])

M2_rref = M2.rref()
print("RREF form:\n", M2_rref[0])

RREF form:
 Matrix([[1, 0, -2, -3], [0, 1, 3, 6]])

Here, one column will not have a pivot → that variable is free.

Try It Yourself

1. Take the system:

   \[ 2x + 3y = 6, \quad 4x + 6y = 12 \]

   Write the augmented matrix and compute its RREF. What does it tell you about solutions?

2. Create a random 3×4 matrix in NumPy. Use SymPy’s Matrix.rref() to compute its reduced form. Identify the pivot columns.

3. For the system:

   \[ x + 2y + 3z = 4, \quad 2x + 4y + 6z = 8 \]

   Check if the equations are independent or multiples of each other by looking at the RREF.

The Takeaway

• REF organizes equations into a staircase shape.
• RREF goes further, making each pivot the only nonzero in its column.
• These canonical forms make it easy to identify pivot variables, free variables, and the solution set structure.

24. Pivots, Free Variables, and Leading Ones (Reading Solutions)

Once a matrix is in row-echelon or reduced row-echelon form, the solutions to the system become visible. The key is identifying pivots, leading ones, and free variables.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. What are pivots?

• A pivot is the first nonzero entry in a row (after elimination).
• In RREF, pivots are scaled to 1 and are called leading ones.
• Pivot columns correspond to basic variables.

2. Example system

\[ \begin{cases} x + y + z = 6 \\ 2x + 3y + z = 10 \end{cases} \]

M = Matrix([
    [1,1,1,6],
    [2,3,1,10]
])

M_rref = M.rref()
print("RREF form:\n", M_rref[0])

RREF form:
 Matrix([[1, 0, 2, 8], [0, 1, -1, -2]])

3. Interpreting the RREF

Suppose the RREF comes out as:

\[ \begin{bmatrix} 1 & 0 & -2 & 4 \\ 0 & 1 & 1 & 2 \end{bmatrix} \]

This means:

• Pivot columns: 1 and 2 → variables \(x\) and \(y\) are basic.

• Free variable: \(z\).

• Equations:

  \[ x - 2z = 4, \quad y + z = 2 \]

• Solution in terms of \(z\):

  \[ x = 4 + 2z, \quad y = 2 - z, \quad z = z \]

4. Coding the solution extraction

rref_matrix, pivots = M_rref
print("Pivot columns:", pivots)

# free variables are the columns not in pivots
all_vars = set(range(rref_matrix.shape[1]-1))  # exclude last column (constants)
free_vars = all_vars - set(pivots)
print("Free variable indices:", free_vars)

Pivot columns: (0, 1)
Free variable indices: {2}

5. Another example with infinitely many solutions

\[ x + 2y + 3z = 4, \quad 2x + 4y + 6z = 8 \]

M2 = Matrix([
    [1,2,3,4],
    [2,4,6,8]
])

M2_rref = M2.rref()
print("RREF form:\n", M2_rref[0])

RREF form:
 Matrix([[1, 2, 3, 4], [0, 0, 0, 0]])

The second row becomes all zeros, showing redundancy. Pivot in column 1, free variables in columns 2 and 3.

6. Solving underdetermined systems

If you have more variables than equations, expect free variables. Example:

\[ x + y = 3 \]

M3 = Matrix([[1,1,3]])
print("RREF form:\n", M3.rref()[0])

RREF form:
 Matrix([[1, 1, 3]])

Here, \(x = 3 - y\). Variable \(y\) is free.

Try It Yourself

1. Take the system:

   \[ x + y + z = 2, \quad y + z = 1 \]

   Compute its RREF and identify pivot and free variables.

2. Create a random 3×4 system and compute its pivots. How many free variables do you get?

3. For the system:

   \[ x - y = 0, \quad 2x - 2y = 0 \]

   Verify that the system has infinitely many solutions and describe them in terms of a free variable.

The Takeaway

• Pivots / leading ones mark the basic variables.
• Free variables correspond to non-pivot columns.
• Solutions are written in terms of free variables, showing whether the system has a unique, infinite, or no solution.

25. Solving Consistent Systems (Unique vs. Infinite Solutions)

Now that we can spot pivots and free variables, we can classify systems of equations as having a unique solution or infinitely many solutions (assuming they’re consistent). In this lab, we’ll practice solving both types.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Unique solution example

System:

\[ x + y = 3, \quad 2x - y = 0 \]

from sympy import Matrix

M = Matrix([
    [1, 1, 3],
    [2, -1, 0]
])

M_rref = M.rref()
print("RREF form:\n", M_rref[0])

# Split into coefficient matrix A and right-hand side b
A = M[:, :2]
b = M[:, 2]

solution = A.solve_least_squares(b)
print("Solution:", solution)

RREF form:
 Matrix([[1, 0, 1], [0, 1, 2]])
Solution: Matrix([[1], [2]])

2. Infinite solution example

System:

\[ x + y + z = 2, \quad 2x + 2y + 2z = 4 \]

M2 = Matrix([
    [1, 1, 1, 2],
    [2, 2, 2, 4]
])

M2_rref = M2.rref()
print("RREF form:\n", M2_rref[0])

RREF form:
 Matrix([[1, 1, 1, 2], [0, 0, 0, 0]])

Only one pivot → two free variables.

Interpretation:

• \(x = 2 - y - z\)
• \(y, z\) are free
• Infinite solutions described by parameters.

3. Classifying consistency

A system is consistent if the RREF does not have a row like:

\[ [0, 0, 0, c] \quad (c \neq 0) \]

Example consistent system:

M3 = Matrix([
    [1, 2, 3],
    [0, 1, 4]
])
print("RREF:\n", M3.rref()[0])

RREF:
 Matrix([[1, 0, -5], [0, 1, 4]])

Example inconsistent system (no solution):

M4 = Matrix([
    [1, 1, 2],
    [2, 2, 5]
])
print("RREF:\n", M4.rref()[0])

RREF:
 Matrix([[1, 1, 0], [0, 0, 1]])

The second one ends with [0,0,1], meaning contradiction (0 = 1).

4. Quick NumPy comparison

For systems with unique solutions:

A = np.array([[1,1],[2,-1]], dtype=float)
b = np.array([3,0], dtype=float)
print("Unique solution with np.linalg.solve:", np.linalg.solve(A,b))

Unique solution with np.linalg.solve: [1. 2.]

For systems with infinite solutions, np.linalg.solve will fail, but SymPy handles parametric solutions.

Try It Yourself

1. Solve:

   \[ x + y + z = 1, \quad 2x + 3y + z = 2 \]

   Is the solution unique or infinite?

2. Check consistency of:

   \[ x + 2y = 3, \quad 2x + 4y = 8 \]

3. Build a random 3×4 augmented matrix and compute its RREF. Identify:

   • Does it have a unique solution, infinitely many, or none?

The Takeaway

• Unique solution: pivot in every variable column.
• Infinite solutions: free variables remain, system is still consistent.
• No solution: an inconsistent row appears.

Understanding pivots and free variables gives a complete picture of the solution set.

26. Detecting Inconsistency (When No Solution Exists)

Not all systems of linear equations can be solved. Some are inconsistent, meaning the equations contradict each other. In this lab, we’ll learn how to recognize inconsistency using augmented matrices and RREF.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. An inconsistent system

\[ x + y = 2, \quad 2x + 2y = 5 \]

Notice the second equation looks like a multiple of the first, but the constant doesn’t match - contradiction.

M = Matrix([
    [1, 1, 2],
    [2, 2, 5]
])

M_rref = M.rref()
print("RREF:\n", M_rref[0])

RREF:
 Matrix([[1, 1, 0], [0, 0, 1]])

RREF gives:

\[ \begin{bmatrix} 1 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \]

The last row means \(0 = 1\), so no solution exists.

2. A consistent system (for contrast)

\[ x + y = 2, \quad 2x + 2y = 4 \]

M2 = Matrix([
    [1, 1, 2],
    [2, 2, 4]
])

print("RREF:\n", M2.rref()[0])

RREF:
 Matrix([[1, 1, 2], [0, 0, 0]])

This reduces to one equation and a redundant row of zeros → infinitely many solutions.

3. Visualizing inconsistency (2D case)

System:

\[ x + y = 2 \quad \text{and} \quad x + y = 3 \]

These are parallel lines that never meet.

import matplotlib.pyplot as plt

x_vals = np.linspace(-1, 3, 100)
y1 = 2 - x_vals
y2 = 3 - x_vals

plt.plot(x_vals, y1, label="x+y=2")
plt.plot(x_vals, y2, label="x+y=3")

plt.legend()
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.show()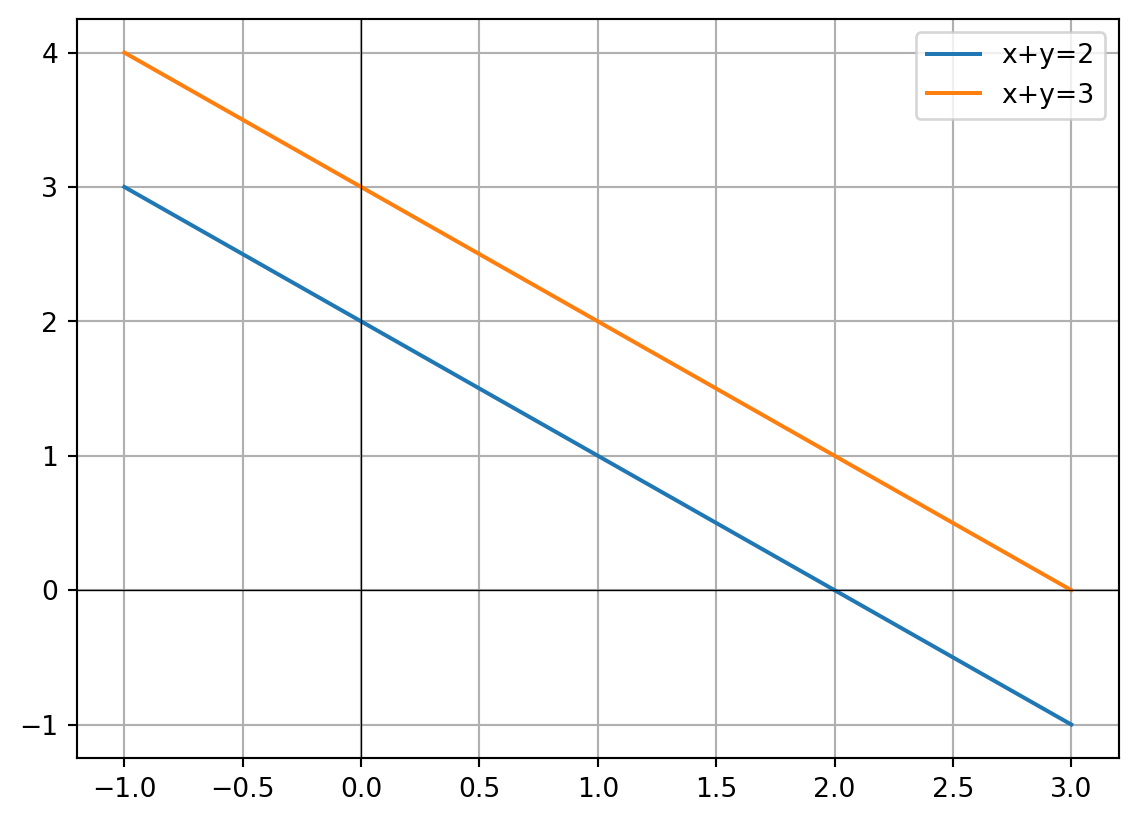

The two lines are parallel → no solution.

4. Detecting inconsistency automatically

We can scan the RREF for a row of the form \([0, 0, …, c]\) with \(c \neq 0\).

def is_inconsistent(M):
    rref_matrix, _ = M.rref()
    for row in rref_matrix.tolist():
        if all(v == 0 for v in row[:-1]) and row[-1] != 0:
            return True
    return False

print("System 1 inconsistent?", is_inconsistent(M))
print("System 2 inconsistent?", is_inconsistent(M2))

System 1 inconsistent? True
System 2 inconsistent? False

Try It Yourself

1. Test the system:

   \[ x + 2y = 4, \quad 2x + 4y = 10 \]

   Write the augmented matrix and check if it’s inconsistent.

2. Build a random 2×3 augmented matrix with integer entries. Use is_inconsistent to check.

3. Plot two linear equations in 2D. Adjust constants to see when they intersect (consistent) vs when they are parallel (inconsistent).

The Takeaway

• A system is inconsistent if RREF contains a row like \([0,0,…,c]\) with \(c \neq 0\).

• Geometrically, this means the equations describe parallel lines (2D), parallel planes (3D), or higher-dimensional contradictions.

• Recognizing inconsistency quickly saves time and avoids chasing impossible solutions.

27. Gaussian Elimination by Hand (A Disciplined Procedure)

Gaussian elimination is the systematic way to solve linear systems using row operations. It transforms the augmented matrix into row-echelon form (REF) and then uses back substitution to find solutions. In this lab, we’ll walk step by step through the process.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Example system

\[ \begin{cases} x + y + z = 6 \\ 2x + 3y + z = 14 \\ x + 2y + 3z = 14 \end{cases} \]

A = np.array([
    [1, 1, 1, 6],
    [2, 3, 1, 14],
    [1, 2, 3, 14]
], dtype=float)

print("Initial augmented matrix:\n", A)

Initial augmented matrix:
 [[ 1.  1.  1.  6.]
 [ 2.  3.  1. 14.]
 [ 1.  2.  3. 14.]]

2. Step 1: Get a pivot in the first column

Make the pivot at (0,0) into 1 (it already is). Now eliminate below it.

A[1] = A[1] - 2*A[0]   # Row2 → Row2 - 2*Row1
A[2] = A[2] - A[0]     # Row3 → Row3 - Row1
print("After eliminating first column:\n", A)

After eliminating first column:
 [[ 1.  1.  1.  6.]
 [ 0.  1. -1.  2.]
 [ 0.  1.  2.  8.]]

3. Step 2: Pivot in the second column

Make the pivot in row 1, col 1 equal to 1.

A[1] = A[1] / A[1,1]
print("After scaling second row:\n", A)

After scaling second row:
 [[ 1.  1.  1.  6.]
 [ 0.  1. -1.  2.]
 [ 0.  1.  2.  8.]]

Now eliminate below:

A[2] = A[2] - A[2,1]*A[1]
print("After eliminating second column:\n", A)

After eliminating second column:
 [[ 1.  1.  1.  6.]
 [ 0.  1. -1.  2.]
 [ 0.  0.  3.  6.]]

4. Step 3: Pivot in the third column

Make the bottom-right entry into 1.

A[2] = A[2] / A[2,2]
print("After scaling third row:\n", A)

After scaling third row:
 [[ 1.  1.  1.  6.]
 [ 0.  1. -1.  2.]
 [ 0.  0.  1.  2.]]

At this point, the matrix is in row-echelon form (REF).

5. Back substitution

Now solve from the bottom up:

z = A[2,3]
y = A[1,3] - A[1,2]*z
x = A[0,3] - A[0,1]*y - A[0,2]*z

print(f"Solution: x={x}, y={y}, z={z}")

Solution: x=0.0, y=4.0, z=2.0

6. Verification

coeff = np.array([
    [1,1,1],
    [2,3,1],
    [1,2,3]
], dtype=float)
const = np.array([6,14,14], dtype=float)

print("Check with np.linalg.solve:", np.linalg.solve(coeff,const))

Check with np.linalg.solve: [0. 4. 2.]

The results match.

Try It Yourself

1. Solve:

   \[ 2x + y = 5, \quad 4x - 6y = -2 \]

   using Gaussian elimination manually in code.

2. Create a random 3×4 augmented matrix and reduce it step by step, printing after each row operation.

3. Compare your manual elimination to SymPy’s RREF with Matrix.rref().

The Takeaway

• Gaussian elimination is a disciplined sequence of row operations.
• It reduces the matrix to row-echelon form, from which back substitution is straightforward.
• This method is the backbone of solving systems by hand and underlies many numerical algorithms.

28. Back Substitution and Solution Sets (Finishing Cleanly)

Once Gaussian elimination reduces a system to row-echelon form (REF), the final step is back substitution. This means solving variables starting from the last equation and working upward. In this lab, we’ll practice both unique and infinite solution cases.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Unique solution example

System:

\[ x + y + z = 6, \quad 2y + 5z = -4, \quad z = 3 \]

Row-echelon form looks like:

\[ \begin{bmatrix} 1 & 1 & 1 & 6 \\ 0 & 2 & 5 & -4 \\ 0 & 0 & 1 & 3 \end{bmatrix} \]

Solve bottom-up:

z = 3
y = (-4 - 5*z)/2
x = 6 - y - z
print(f"Solution: x={x}, y={y}, z={z}")

Solution: x=12.5, y=-9.5, z=3

2. Infinite solution example

System:

\[ x + y + z = 2, \quad 2x + 2y + 2z = 4 \]

After elimination:

\[ \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \]

This means:

• Equation: \(x + y + z = 2\).
• Free variables: choose \(y\) and \(z\).

Let \(y = s, z = t\). Then:

\[ x = 2 - s - t \]

So the solution set is:

from sympy import symbols
s, t = symbols('s t')
x = 2 - s - t
y = s
z = t
print("General solution:")
print("x =", x, ", y =", y, ", z =", z)

General solution:
x = -s - t + 2 , y = s , z = t

3. Consistency check with RREF

We can use SymPy to confirm solution sets:

M = Matrix([
    [1,1,1,2],
    [2,2,2,4]
])

print("RREF form:\n", M.rref()[0])

RREF form:
 Matrix([[1, 1, 1, 2], [0, 0, 0, 0]])

The second row disappears, showing infinite solutions.

4. Encoding solution sets

General solutions are often written in parametric vector form.

For the infinite solution above:

\[ (x,y,z) = (2,0,0) + s(-1,1,0) + t(-1,0,1) \]

This shows the solution space is a plane in \(\mathbb{R}^3\).

Try It Yourself

1. Solve:

   \[ x + 2y = 5, \quad y = 1 \]

   Do back substitution by hand and check with NumPy.

2. Take the system:

   \[ x + y + z = 1, \quad 2x + 2y + 2z = 2 \]

   Write its solution set in parametric form.

3. Use Matrix.rref() on a 3×4 random augmented matrix. Identify pivot and free variables, then describe the solution set.

The Takeaway

• Back substitution is the cleanup step after Gaussian elimination.
• It reveals whether the system has a unique solution or infinitely many.
• Solutions can be expressed explicitly (unique case) or parametrically (infinite case).

29. Rank and Its First Meaning (Pivots as Information)

The rank of a matrix tells us how much independent information it contains. Rank is one of the most important concepts in linear algebra because it connects to pivots, independence, dimension, and the number of solutions to a system.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Rank definition The rank is the number of pivots (leading ones) in the row-echelon form of a matrix.

Example:

A = Matrix([
    [1, 2, 3],
    [2, 4, 6],
    [1, 1, 1]
])

print("RREF:\n", A.rref()[0])
print("Rank of A:", A.rank())

RREF:
 Matrix([[1, 0, -1], [0, 1, 2], [0, 0, 0]])
Rank of A: 2

• The second row is a multiple of the first, so the rank is less than 3.
• Only two independent rows → rank = 2.

2. Rank and solutions to \(A·x = b\)

Consider:

\[ \begin{cases} x + y + z = 3 \\ 2x + 2y + 2z = 6 \\ x - y = 0 \end{cases} \]

M = Matrix([
    [1, 1, 1, 3],
    [2, 2, 2, 6],
    [1, -1, 0, 0]
])

print("RREF:\n", M.rref()[0])
print("Rank of coefficient matrix:", M[:, :-1].rank())
print("Rank of augmented matrix:", M.rank())

RREF:
 Matrix([[1, 0, 1/2, 3/2], [0, 1, 1/2, 3/2], [0, 0, 0, 0]])
Rank of coefficient matrix: 2
Rank of augmented matrix: 2

• If rank(A) = rank([A|b]) = number of variables → unique solution.
• If rank(A) = rank([A|b]) < number of variables → infinite solutions.
• If rank(A) < rank([A|b]) → no solution.

3. NumPy comparison

A = np.array([
    [1, 2, 3],
    [2, 4, 6],
    [1, 1, 1]
], dtype=float)

print("Rank with NumPy:", np.linalg.matrix_rank(A))

Rank with NumPy: 2

4. Rank as “dimension of information”

The rank equals:

• The number of independent rows.
• The number of independent columns.
• The dimension of the column space.

B = Matrix([
    [1,2],
    [2,4],
    [3,6]
])

print("Rank of B:", B.rank())

Rank of B: 1

All columns are multiples → only one independent direction → rank = 1.

Try It Yourself

1. Compute the rank of:

   \[ \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{bmatrix} \]

   What do you expect?

2. Create a random 4×4 matrix with np.random.randint. Compute its rank with both SymPy and NumPy.

3. Test solution consistency using rank: build a system where rank(A) ≠ rank([A|b]) and show it has no solution.

The Takeaway

• Rank = number of pivots = dimension of independent information.
• Rank reveals whether a system has no solution, one solution, or infinitely many.
• Rank connects algebra (pivots) with geometry (dimension of subspaces).

30. LU Factorization (Elimination Captured as L and U)

Gaussian elimination can be recorded in a neat factorization:

\[ A = LU \]

where \(L\) is a lower triangular matrix (recording the multipliers we used) and \(U\) is an upper triangular matrix (the result of elimination). This is called LU factorization. It’s a powerful tool for solving systems efficiently.

Set Up Your Lab

import numpy as np
from scipy.linalg import lu

Step-by-Step Code Walkthrough

1. Example matrix

A = np.array([
    [2, 3, 1],
    [4, 7, 7],
    [6, 18, 22]
], dtype=float)

print("Matrix A:\n", A)

Matrix A:
 [[ 2.  3.  1.]
 [ 4.  7.  7.]
 [ 6. 18. 22.]]

2. LU decomposition with SciPy

P, L, U = lu(A)

print("Permutation matrix P:\n", P)
print("Lower triangular L:\n", L)
print("Upper triangular U:\n", U)

Permutation matrix P:
 [[0. 0. 1.]
 [0. 1. 0.]
 [1. 0. 0.]]
Lower triangular L:
 [[1.         0.         0.        ]
 [0.66666667 1.         0.        ]
 [0.33333333 0.6        1.        ]]
Upper triangular U:
 [[ 6.         18.         22.        ]
 [ 0.         -5.         -7.66666667]
 [ 0.          0.         -1.73333333]]

Here, \(P\) handles row swaps (partial pivoting), \(L\) is lower triangular, and \(U\) is upper triangular.

3. Verifying the factorization

reconstructed = P @ L @ U
print("Does P·L·U equal A?\n", np.allclose(reconstructed, A))

Does P·L·U equal A?
 True

4. Solving a system with LU

Suppose we want to solve \(Ax = b\). Instead of working directly with \(A\), we solve in two steps:

1. Solve \(Ly = Pb\) (forward substitution).
2. Solve \(Ux = y\) (back substitution).

b = np.array([1, 2, 3], dtype=float)

# Step 1: Pb
Pb = P @ b

# Step 2: forward substitution Ly = Pb
y = np.linalg.solve(L, Pb)

# Step 3: back substitution Ux = y
x = np.linalg.solve(U, y)

print("Solution x:", x)

Solution x: [ 0.5 -0.  -0. ]

5. Efficiency advantage

If we have to solve many systems with the same \(A\) but different \(b\), we only compute \(LU\) once, then reuse it. This saves a lot of computation.

6. NumPy’s built-in rank-revealing factorization

While NumPy doesn’t have lu directly, it works seamlessly with SciPy. For large matrices, LU decomposition is the backbone of solvers like np.linalg.solve.

Try It Yourself

1. Compute LU decomposition for

   \[ A = \begin{bmatrix} 1 & 2 & 0 \\ 3 & 4 & 4 \\ 5 & 6 & 3 \end{bmatrix} \]

   Verify \(P·L·U = A\).

2. Solve \(Ax = b\) with

   \[ b = [3,7,8] \]

   using LU factorization.

3. Compare solving with LU factorization vs directly using np.linalg.solve(A,b). Are the answers the same?

The Takeaway

• LU factorization captures Gaussian elimination in matrix form: \(A = P·L·U\).
• It allows fast repeated solving of systems with different right-hand sides.
• LU decomposition is a core technique in numerical linear algebra and the basis of many solvers.

Chapter 4. Vector Spaces and Subspaces

31. Axioms of Vector Spaces (What “Space” Really Means)

Vector spaces generalize what we’ve been doing with vectors and matrices. Instead of just \(\mathbb{R}^n\), a vector space is any collection of objects (vectors) where addition and scalar multiplication follow specific axioms (rules). In this lab, we’ll explore these axioms concretely with Python.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Vector space example: \(\mathbb{R}^2\)

Let’s check two rules (axioms): closure under addition and scalar multiplication.

u = np.array([1, 2])
v = np.array([3, -1])

# Closure under addition
print("u + v =", u + v)

# Closure under scalar multiplication
k = 5
print("k * u =", k * u)

u + v = [4 1]
k * u = [ 5 10]

Both results are still in \(\mathbb{R}^2\).

2. Zero vector and additive inverses

Every vector space must contain a zero vector, and every vector must have an additive inverse.

zero = np.array([0, 0])
inverse_u = -u
print("Zero vector:", zero)
print("u + (-u) =", u + inverse_u)

Zero vector: [0 0]
u + (-u) = [0 0]

3. Distributive and associative properties

Check:

• \(a(u+v) = au + av\)
• \((a+b)u = au + bu\)

a, b = 2, 3

lhs1 = a * (u + v)
rhs1 = a*u + a*v
print("a(u+v) =", lhs1, ", au+av =", rhs1)

lhs2 = (a+b) * u
rhs2 = a*u + b*u
print("(a+b)u =", lhs2, ", au+bu =", rhs2)

a(u+v) = [8 2] , au+av = [8 2]
(a+b)u = [ 5 10] , au+bu = [ 5 10]

Both equalities hold → distributive laws confirmed.

4. A set that fails to be a vector space

Consider only positive numbers with normal addition and scalar multiplication.

positive_numbers = [1, 2, 3]
try:
    print("Closure under negatives?", -1 * np.array(positive_numbers))
except Exception as e:
    print("Error:", e)

Closure under negatives? [-1 -2 -3]

Negative results leave the set → not a vector space.

5. Python helper to check axioms

We can quickly check if a set of vectors is closed under addition and scalar multiplication.

def check_closure(vectors, scalars):
    for v in vectors:
        for u in vectors:
            if not any(np.array_equal(v+u, w) for w in vectors):
                return False
        for k in scalars:
            if not any(np.array_equal(k*v, w) for w in vectors):
                return False
    return True

vectors = [np.array([0,0]), np.array([1,0]), np.array([0,1]), np.array([1,1])]
scalars = [0,1,-1]
print("Closed under addition and scalar multiplication?", check_closure(vectors, scalars))

Closed under addition and scalar multiplication? False

This small set is closed → it forms a vector space (a subspace of \(\mathbb{R}^2\)).

Try It Yourself

1. Verify that \(\mathbb{R}^3\) satisfies the vector space axioms using random vectors.
2. Test whether the set of all 2×2 matrices forms a vector space under normal addition and scalar multiplication.
3. Find an example of a set that fails closure (e.g., integers under division).

The Takeaway

• A vector space is any set where addition and scalar multiplication satisfy 10 standard axioms.
• These rules ensure consistent algebraic behavior.
• Many objects beyond arrows in \(\mathbb{R}^n\) (like polynomials or matrices) are vector spaces too.

32. Subspaces, Column Space, and Null Space (Where Solutions Live)

A subspace is a smaller vector space sitting inside a bigger one. For matrices, two subspaces show up all the time:

• Column space: all combinations of the matrix’s columns (possible outputs of \(Ax\)).
• Null space: all vectors \(x\) such that \(Ax = 0\) (inputs that vanish).

This lab explores both in Python.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Column space basics

Take:

\[ A = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 3 & 6 \end{bmatrix} \]

A = Matrix([
    [1,2],
    [2,4],
    [3,6]
])

print("Matrix A:\n", A)
print("Column space basis:\n", A.columnspace())
print("Rank (dimension of column space):", A.rank())

Matrix A:
 Matrix([[1, 2], [2, 4], [3, 6]])
Column space basis:
 [Matrix([
[1],
[2],
[3]])]
Rank (dimension of column space): 1

• The second column is a multiple of the first → column space has dimension 1.
• All outputs of \(Ax\) lie on a line in \(\mathbb{R}^3\).

2. Null space basics

print("Null space basis:\n", A.nullspace())

Null space basis:
 [Matrix([
[-2],
[ 1]])]

The null space contains all \(x\) where \(Ax=0\). Here, the null space is 1-dimensional (vectors like \([-2,1]\)).

3. A full-rank example

B = Matrix([
    [1,0,0],
    [0,1,0],
    [0,0,1]
])

print("Column space basis:\n", B.columnspace())
print("Null space basis:\n", B.nullspace())

Column space basis:
 [Matrix([
[1],
[0],
[0]]), Matrix([
[0],
[1],
[0]]), Matrix([
[0],
[0],
[1]])]
Null space basis:
 []

• Column space = all of \(\mathbb{R}^3\).
• Null space = only the zero vector.

4. Geometry link

For \(A\) (rank 1, 2 columns):

• Column space: line in \(\mathbb{R}^3\).
• Null space: line in \(\mathbb{R}^2\).

Together they explain the system \(Ax = b\):

• If \(b\) is outside the column space, no solution exists.
• If \(b\) is inside, solutions differ by a vector in the null space.

5. Quick NumPy version

NumPy doesn’t directly give null space, but we can compute it with SVD.

from numpy.linalg import svd

A = np.array([[1,2],[2,4],[3,6]], dtype=float)
U, S, Vt = svd(A)

tol = 1e-10
null_mask = (S <= tol)
null_space = Vt.T[:, null_mask]
print("Null space (via SVD):\n", null_space)

Null space (via SVD):
 [[-0.89442719]
 [ 0.4472136 ]]

Try It Yourself

1. Find the column space and null space of

   \[ \begin{bmatrix} 1 & 1 \\ 0 & 1 \\ 0 & 0 \end{bmatrix} \]

   How many dimensions does each have?

2. Generate a random 3×3 matrix. Compute its rank, column space, and null space.

3. Solve \(Ax = b\) with

   \[ A = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 3 & 6 \end{bmatrix}, \quad b = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \]

   and describe why it has infinitely many solutions.

The Takeaway

• The column space = all possible outputs of a matrix.
• The null space = all inputs that map to zero.
• These subspaces give the complete picture of what a matrix does.

33. Span and Generating Sets (Coverage of a Space)

The span of a set of vectors is all the linear combinations you can make from them. If a set of vectors can “cover” a whole space, we call it a generating set. This lab shows how to compute and visualize spans.

Set Up Your Lab

import numpy as np
from sympy import Matrix
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Span in \(\mathbb{R}^2\)

Two vectors that aren’t multiples span the whole plane.

u = np.array([1, 0])
v = np.array([0, 1])

M = Matrix.hstack(Matrix(u), Matrix(v))
print("Rank:", M.rank())

Rank: 2

Rank = 2 → the span of \(\{u,v\}\) is all of \(\mathbb{R}^2\).

2. Dependent vectors (smaller span)

u = np.array([1, 2])
v = np.array([2, 4])

M = Matrix.hstack(Matrix(u), Matrix(v))
print("Rank:", M.rank())

Rank: 1

Rank = 1 → these vectors only span a line.

3. Visualizing a span

Let’s see what the span of two vectors looks like.

u = np.array([1, 2])
v = np.array([2, 1])

coeffs = np.linspace(-2, 2, 11)
points = []
for a in coeffs:
    for b in coeffs:
        points.append(a*u + b*v)
points = np.array(points)

plt.scatter(points[:,0], points[:,1], s=10)
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.title("Span of {u,v}")
plt.grid()
plt.show()

You’ll see a filled grid - the entire plane, because the two vectors are independent.

4. Generating set of a space

For \(\mathbb{R}^3\):

basis = [Matrix([1,0,0]), Matrix([0,1,0]), Matrix([0,0,1])]
M = Matrix.hstack(*basis)
print("Rank:", M.rank())

Rank: 3

Rank = 3 → this set spans the whole space.

5. Testing if a vector is in the span

Example: Is \([3,5]\) in the span of \([1,2]\) and \([2,1]\)?

u = Matrix([1,2])
v = Matrix([2,1])
target = Matrix([3,5])

M = Matrix.hstack(u,v)
solution = M.gauss_jordan_solve(target)
print("Coefficients (a,b):", solution)

Coefficients (a,b): (Matrix([
[7/3],
[1/3]]), Matrix(0, 1, []))

If a solution exists, the target is in the span.

Try It Yourself

1. Test if \([4,6]\) is in the span of \([1,2]\).
2. Visualize the span of \([1,0,0]\) and \([0,1,0]\) in \(\mathbb{R}^3\). What does it look like?
3. Create a random 3×3 matrix. Use rank() to check if its columns span \(\mathbb{R}^3\).

The Takeaway

• Span = all linear combinations of a set of vectors.
• Independent vectors span bigger spaces; dependent ones collapse to smaller spaces.
• Generating sets are the foundation of bases and coordinate systems.

34. Linear Independence and Dependence (No Redundancy vs. Redundancy)

A set of vectors is linearly independent if none of them can be written as a combination of the others. If at least one can, the set is dependent. This distinction tells us whether a set of vectors has redundancy.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Independent vectors example

v1 = Matrix([1, 0, 0])
v2 = Matrix([0, 1, 0])
v3 = Matrix([0, 0, 1])

M = Matrix.hstack(v1, v2, v3)
print("Rank:", M.rank(), " Number of vectors:", M.shape[1])

Rank: 3  Number of vectors: 3

Rank = 3, number of vectors = 3 → all independent.

2. Dependent vectors example

v1 = Matrix([1, 2, 3])
v2 = Matrix([2, 4, 6])
v3 = Matrix([3, 6, 9])

M = Matrix.hstack(v1, v2, v3)
print("Rank:", M.rank(), " Number of vectors:", M.shape[1])

Rank: 1  Number of vectors: 3

Rank = 1, number of vectors = 3 → they’re dependent (multiples of each other).

3. Checking dependence automatically

A quick test: if rank < number of vectors → dependent.

def check_independence(vectors):
    M = Matrix.hstack(*vectors)
    return M.rank() == M.shape[1]

print("Independent?", check_independence([Matrix([1,0]), Matrix([0,1])]))
print("Independent?", check_independence([Matrix([1,2]), Matrix([2,4])]))

Independent? True
Independent? False

4. Solving for dependence relation

If vectors are dependent, we can find coefficients \(c_1, c_2, …\) such that

\[ c_1 v_1 + c_2 v_2 + … + c_k v_k = 0 \]

with some \(c_i \neq 0\).

M = Matrix.hstack(Matrix([1,2]), Matrix([2,4]))
null_space = M.nullspace()
print("Dependence relation (coefficients):", null_space)

Dependence relation (coefficients): [Matrix([
[-2],
[ 1]])]

This shows the exact linear relation.

5. Random example

np.random.seed(0)
R = Matrix(np.random.randint(-3, 4, (3,3)))
print("Random matrix:\n", R)
print("Rank:", R.rank())

Random matrix:
 Matrix([[1, 2, -3], [0, 0, 0], [-2, 0, 2]])
Rank: 2

Depending on the rank, the columns may be independent (rank = 3) or dependent (rank < 3).

Try It Yourself

1. Test if \([1,1,0], [0,1,1], [1,2,1]\) are independent.
2. Generate 4 random vectors in \(\mathbb{R}^3\). Can they ever be independent? Why or why not?
3. Find the dependence relation for \([2,4], [3,6]\).

The Takeaway

• Independent set: no redundancy, each vector adds a new direction.
• Dependent set: at least one vector is unnecessary (it lies in the span of others).
• Independence is the key to defining basis and dimension.

35. Basis and Coordinates (Naming Every Vector Uniquely)

A basis is a set of independent vectors that span a space. It’s like choosing a coordinate system: every vector in the space can be expressed uniquely as a combination of basis vectors. In this lab, we’ll see how to find bases and compute coordinates relative to them.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Standard basis in \(\mathbb{R}^3\)

e1 = Matrix([1,0,0])
e2 = Matrix([0,1,0])
e3 = Matrix([0,0,1])

M = Matrix.hstack(e1, e2, e3)
print("Rank:", M.rank())

Rank: 3

These three independent vectors form the standard basis of \(\mathbb{R}^3\). Any vector like \([2,5,-1]\) can be expressed as

\[ 2e_1 + 5e_2 - 1e_3 \]

2. Finding a basis from dependent vectors

v1 = Matrix([1,2,3])
v2 = Matrix([2,4,6])
v3 = Matrix([1,0,1])

M = Matrix.hstack(v1,v2,v3)
print("Column space basis:", M.columnspace())

Column space basis: [Matrix([
[1],
[2],
[3]]), Matrix([
[1],
[0],
[1]])]

SymPy extracts independent columns automatically. This gives a basis for the column space.

3. Coordinates relative to a basis

Suppose basis = \(\{ [1,0], [1,1] \}\). Express vector \([3,5]\) in this basis.

B = Matrix.hstack(Matrix([1,0]), Matrix([1,1]))
target = Matrix([3,5])

coords = B.solve_least_squares(target)
print("Coordinates in basis B:", coords)

Coordinates in basis B: Matrix([[-2], [5]])

So \([3,5] = 3·[1,0] + 2·[1,1]\).

4. Basis change

If we switch to a different basis, coordinates change but the vector stays the same.

new_basis = Matrix.hstack(Matrix([2,1]), Matrix([1,2]))
coords_new = new_basis.solve_least_squares(target)
print("Coordinates in new basis:", coords_new)

Coordinates in new basis: Matrix([[1/3], [7/3]])

5. Random example

Generate 3 random vectors in \(\mathbb{R}^3\). Check if they form a basis.

np.random.seed(1)
R = Matrix(np.random.randint(-3,4,(3,3)))
print("Random matrix:\n", R)
print("Rank:", R.rank())

Random matrix:
 Matrix([[2, 0, 1], [-3, -2, 0], [2, -3, -3]])
Rank: 3

If rank = 3 → basis for \(\mathbb{R}^3\). Otherwise, only span a subspace.

Try It Yourself

1. Check if \([1,2], [3,4]\) form a basis of \(\mathbb{R}^2\).
2. Express vector \([7,5]\) in that basis.
3. Create 4 random vectors in \(\mathbb{R}^3\). Find a basis for their span.

The Takeaway

• A basis = minimal set of vectors that span a space.
• Every vector has a unique coordinate representation in a given basis.
• Changing bases changes the coordinates, not the vector itself.

36. Dimension (How Many Directions)

The dimension of a vector space is the number of independent directions it has. Formally, it’s the number of vectors in any basis of the space. Dimension tells us the “size” of a space in terms of degrees of freedom.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Dimension of \(\mathbb{R}^n\)

The dimension of \(\mathbb{R}^n\) is \(n\).

n = 4
basis = [Matrix.eye(n)[:,i] for i in range(n)]
print("Basis for R^4:", basis)
print("Dimension of R^4:", len(basis))

Basis for R^4: [Matrix([
[1],
[0],
[0],
[0]]), Matrix([
[0],
[1],
[0],
[0]]), Matrix([
[0],
[0],
[1],
[0]]), Matrix([
[0],
[0],
[0],
[1]])]
Dimension of R^4: 4

Each standard unit vector adds one independent direction → dimension = 4.

2. Dimension via rank

The rank of a matrix equals the dimension of its column space.

A = Matrix([
    [1,2,3],
    [2,4,6],
    [1,0,1]
])

print("Rank (dimension of column space):", A.rank())

Rank (dimension of column space): 2

Here, rank = 2 → the column space is a 2D plane inside \(\mathbb{R}^3\).

3. Null space dimension

The null space dimension is given by:

\[ \text{dim(Null(A))} = \#\text{variables} - \text{rank(A)} \]

print("Null space basis:", A.nullspace())
print("Dimension of null space:", len(A.nullspace()))

Null space basis: [Matrix([
[-1],
[-1],
[ 1]])]
Dimension of null space: 1

This is the number of free variables in a solution.

4. Dimension in practice

• A line through the origin in \(\mathbb{R}^3\) has dimension 1.
• A plane through the origin has dimension 2.
• The whole \(\mathbb{R}^3\) has dimension 3.

Example:

v1 = Matrix([1,2,3])
v2 = Matrix([2,4,6])
span = Matrix.hstack(v1,v2)
print("Dimension of span:", span.rank())

Dimension of span: 1

Result = 1 → they only generate a line.

5. Random example

np.random.seed(2)
R = Matrix(np.random.randint(-3,4,(4,4)))
print("Random 4x4 matrix:\n", R)
print("Column space dimension:", R.rank())

Random 4x4 matrix:
 Matrix([[-3, 2, -3, 3], [0, -1, 0, -3], [-1, -2, 0, 2], [-1, 1, 1, 1]])
Column space dimension: 4

Rank may be 4 (full space) or smaller (collapsed).

Try It Yourself

1. Find the dimension of the column space of

   \[ \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \]

2. Compute the dimension of the null space of a 3×3 singular matrix.

3. Generate a 5×3 random matrix and compute its column space dimension.

The Takeaway

• Dimension = number of independent directions.
• Found by counting basis vectors (or rank).
• Dimensions describe lines (1D), planes (2D), and higher subspaces inside larger spaces.

37. Rank–Nullity Theorem (Dimensions That Add Up)

The rank–nullity theorem ties together the dimension of the column space and the null space of a matrix. It says:

\[ \text{rank}(A) + \text{nullity}(A) = \text{number of columns of } A \]

This is a powerful consistency check in linear algebra.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Simple 3×3 example

A = Matrix([
    [1, 2, 3],
    [2, 4, 6],
    [1, 0, 1]
])

rank = A.rank()
nullity = len(A.nullspace())
print("Rank:", rank)
print("Nullity:", nullity)
print("Rank + Nullity =", rank + nullity)
print("Number of columns =", A.shape[1])

Rank: 2
Nullity: 1
Rank + Nullity = 3
Number of columns = 3

You should see that rank + nullity = 3, the number of columns.

2. Full-rank case

B = Matrix([
    [1,0,0],
    [0,1,0],
    [0,0,1]
])

print("Rank:", B.rank())
print("Nullity:", len(B.nullspace()))

Rank: 3
Nullity: 0

• Rank = 3 (all independent).
• Nullity = 0 (only zero solution to \(Bx=0\)).
• Rank + Nullity = 3 columns.

3. Wide matrix (more columns than rows)

C = Matrix([
    [1,2,3,4],
    [0,1,1,2],
    [0,0,0,0]
])

rank = C.rank()
nullity = len(C.nullspace())
print("Rank:", rank, " Nullity:", nullity, " Columns:", C.shape[1])

Rank: 2  Nullity: 2  Columns: 4

Here, nullity > 0 because there are more variables than independent equations.

4. Verifying with random matrices

np.random.seed(3)
R = Matrix(np.random.randint(-3,4,(4,5)))
print("Random 4x5 matrix:\n", R)
print("Rank + Nullity =", R.rank() + len(R.nullspace()))
print("Number of columns =", R.shape[1])

Random 4x5 matrix:
 Matrix([[-1, -3, -2, 0, -3], [-3, -3, 2, 2, 0], [-1, 0, -2, -2, -1], [2, 3, -3, 1, 1]])
Rank + Nullity = 5
Number of columns = 5

Always consistent: rank + nullity = number of columns.

5. Geometric interpretation

For an \(m \times n\) matrix:

• Rank(A) = dimension of outputs (column space).
• Nullity(A) = dimension of hidden directions that collapse to 0.
• Together, they use up all the “input dimensions” (n).

Try It Yourself

1. Compute rank and nullity of

   \[ \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix} \]

   Check the theorem.

2. Create a 2×4 random integer matrix. Confirm that rank + nullity = 4.

3. Explain why a tall full-rank \(5 \times 3\) matrix must have nullity = 0.

The Takeaway

• Rank + Nullity = number of columns (always true).
• Rank measures independent outputs; nullity measures hidden freedom.
• This theorem connects solutions of \(Ax=0\) with the structure of \(A\).

38. Coordinates Relative to a Basis (Changing the “Ruler”)

Once we choose a basis, every vector can be described with coordinates relative to that basis. This is like changing the “ruler” we use to measure vectors. In this lab, we’ll practice computing coordinates in different bases.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Standard basis coordinates

Vector \(v = [4,5]\) in \(\mathbb{R}^2\):

v = Matrix([4,5])
e1 = Matrix([1,0])
e2 = Matrix([0,1])

B = Matrix.hstack(e1,e2)
coords = B.solve_least_squares(v)
print("Coordinates in standard basis:", coords)

Coordinates in standard basis: Matrix([[4], [5]])

Result is just \([4,5]\). Easy - the standard basis matches the components directly.

2. Non-standard basis

Suppose basis = \(\{ [1,1], [1,-1] \}\). Express \(v = [4,5]\) in this basis.

B2 = Matrix.hstack(Matrix([1,1]), Matrix([1,-1]))
coords2 = B2.solve_least_squares(v)
print("Coordinates in new basis:", coords2)

Coordinates in new basis: Matrix([[9/2], [-1/2]])

Now \(v\) has different coordinates.

3. Changing coordinates back

To reconstruct the vector from coordinates:

reconstructed = B2 * coords2
print("Reconstructed vector:", reconstructed)

Reconstructed vector: Matrix([[4], [5]])

It matches the original \([4,5]\).

4. Random basis in \(\mathbb{R}^3\)

basis = Matrix.hstack(
    Matrix([1,0,1]),
    Matrix([0,1,1]),
    Matrix([1,1,0])
)
v = Matrix([2,3,4])

coords = basis.solve_least_squares(v)
print("Coordinates of v in random basis:", coords)

Coordinates of v in random basis: Matrix([[3/2], [5/2], [1/2]])

Any independent set of 3 vectors in \(\mathbb{R}^3\) works as a basis.

5. Visualization in 2D

Let’s compare coordinates in two bases.

import matplotlib.pyplot as plt

v = np.array([4,5])
b1 = np.array([1,1])
b2 = np.array([1,-1])

plt.quiver(0,0,v[0],v[1],angles='xy',scale_units='xy',scale=1,color='blue',label='v')
plt.quiver(0,0,b1[0],b1[1],angles='xy',scale_units='xy',scale=1,color='red',label='basis1')
plt.quiver(0,0,b2[0],b2[1],angles='xy',scale_units='xy',scale=1,color='green',label='basis2')

plt.xlim(-1,6)
plt.ylim(-6,6)
plt.legend()
plt.grid()
plt.show()

Even though the basis vectors look different, they span the same space, and \(v\) can be expressed in terms of them.

Try It Yourself

1. Express \([7,3]\) in the basis \(\{[2,0], [0,3]\}\).
2. Pick three independent random vectors in \(\mathbb{R}^3\). Write down the coordinates of \([1,2,3]\) in that basis.
3. Verify that reconstructing always gives the original vector.

The Takeaway

• A basis provides a coordinate system for vectors.
• Coordinates depend on the basis, but the underlying vector doesn’t change.
• Changing the basis is like changing the “ruler” you measure vectors with.

39. Change-of-Basis Matrices (Moving Between Coordinate Systems)

When we switch from one basis to another, we need a change-of-basis matrix. This matrix acts like a translator: it converts coordinates in one system to coordinates in another.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Two bases in \(\mathbb{R}^2\)

Let’s define:

• Basis \(B = \{ [1,0], [0,1] \}\) (standard basis).
• Basis \(C = \{ [1,1], [1,-1] \}\).

B = Matrix.hstack(Matrix([1,0]), Matrix([0,1]))
C = Matrix.hstack(Matrix([1,1]), Matrix([1,-1]))

2. Change-of-basis matrix

The matrix that converts C-coordinates → standard coordinates is just \(C\).

print("C (basis matrix):\n", C)

C (basis matrix):
 Matrix([[1, 1], [1, -1]])

To go the other way (standard → C), we compute the inverse of \(C\).

C_inv = C.inv()
print("C inverse:\n", C_inv)

C inverse:
 Matrix([[1/2, 1/2], [1/2, -1/2]])

3. Converting coordinates

Vector \(v = [4,5]\).

• In standard basis:

v = Matrix([4,5])
coords_in_standard = v
print("Coordinates in standard basis:", coords_in_standard)

Coordinates in standard basis: Matrix([[4], [5]])

• In basis \(C\):

coords_in_C = C_inv * v
print("Coordinates in C basis:", coords_in_C)

Coordinates in C basis: Matrix([[9/2], [-1/2]])

• Convert back:

reconstructed = C * coords_in_C
print("Reconstructed vector:", reconstructed)

Reconstructed vector: Matrix([[4], [5]])

The reconstruction matches the original vector.

4. General formula

If \(P\) is the change-of-basis matrix from basis \(B\) to basis \(C\):

\[ [v]_C = P^{-1}[v]_B \]

\[ [v]_B = P[v]_C \]

Here, \(P\) is the matrix of new basis vectors written in terms of the old basis.

5. Random 3D example

B = Matrix.eye(3)  # standard basis
C = Matrix.hstack(
    Matrix([1,0,1]),
    Matrix([0,1,1]),
    Matrix([1,1,0])
)

v = Matrix([2,3,4])

C_inv = C.inv()
coords_in_C = C_inv * v
print("Coordinates in new basis C:", coords_in_C)

print("Back to standard:", C * coords_in_C)

Coordinates in new basis C: Matrix([[3/2], [5/2], [1/2]])
Back to standard: Matrix([[2], [3], [4]])

Try It Yourself

1. Convert \([7,3]\) from the standard basis to the basis \(\{[2,0], [0,3]\}\).
2. Pick a random invertible 3×3 matrix as a basis. Write a vector in that basis, then convert it back to the standard basis.
3. Prove that converting back and forth always returns the same vector.

The Takeaway

• A change-of-basis matrix converts coordinates between bases.
• Going from new basis → old basis uses the basis matrix.
• Going from old basis → new basis requires its inverse.
• The vector itself never changes - only the description of it does.

40. Affine Subspaces (Lines and Planes Not Through the Origin)

So far, subspaces always passed through the origin. But many familiar objects - like lines offset from the origin or planes floating in space - are affine subspaces. They look like subspaces, just shifted away from zero.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Line through the origin (a subspace)

\[ L = \{ t \cdot [1,2] : t \in \mathbb{R} \} \]

t = np.linspace(-3,3,20)
line_origin = np.array([t, 2*t]).T
plt.plot(line_origin[:,0], line_origin[:,1], label="Through origin")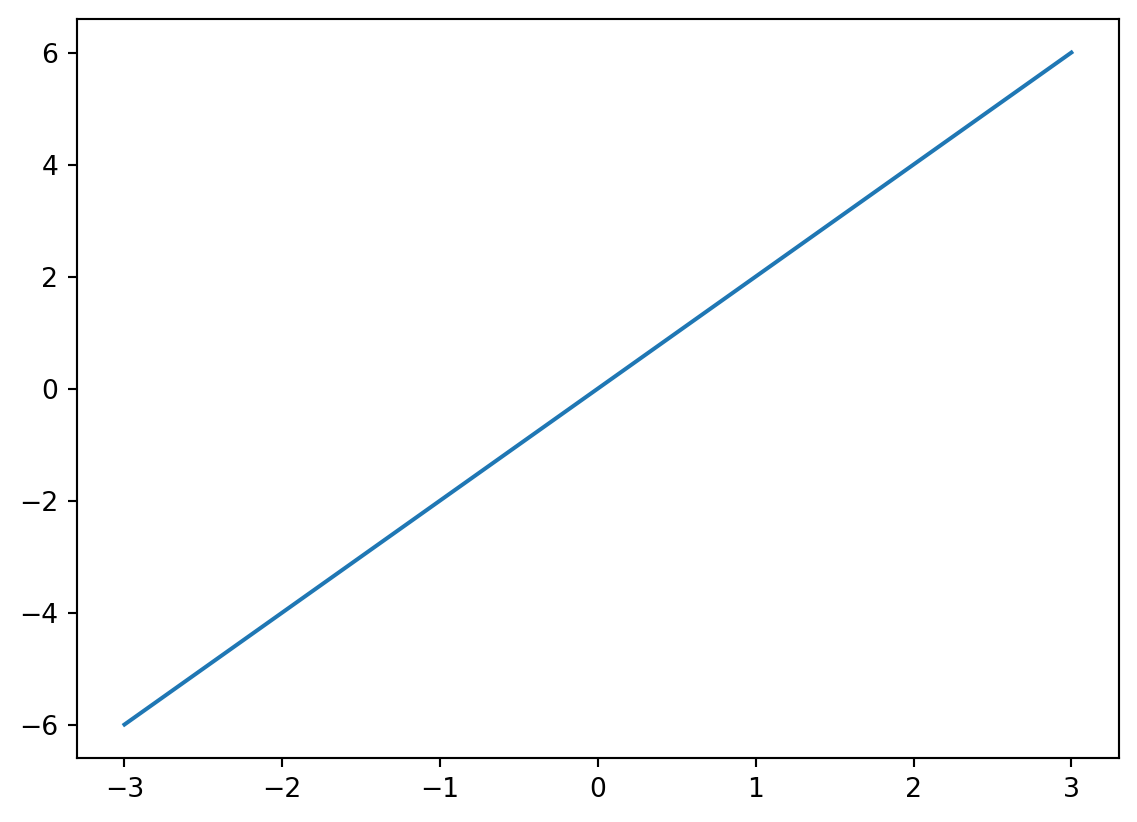

2. Line not through the origin (affine subspace)

\[ L' = \{ [3,1] + t \cdot [1,2] : t \in \mathbb{R} \} \]

point = np.array([3,1])
direction = np.array([1,2])
line_shifted = np.array([point + k*direction for k in t])
plt.plot(line_shifted[:,0], line_shifted[:,1], label="Shifted line")

3. Visualizing together

plt.scatter(*point, color="red", label="Shift point")
plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.legend()
plt.grid()
plt.show()

One line passes through the origin, the other is parallel but shifted.

4. Plane example

A plane in \(\mathbb{R}^3\):

\[ P = \{ [1,2,3] + s[1,0,0] + t[0,1,0] : s,t \in \mathbb{R} \} \]

This is an affine plane parallel to the \(xy\)-plane, but shifted.

s_vals = np.linspace(-2,2,10)
t_vals = np.linspace(-2,2,10)

points = []
for s in s_vals:
    for t in t_vals:
        points.append([1,2,3] + s*np.array([1,0,0]) + t*np.array([0,1,0]))

points = np.array(points)

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(points[:,0], points[:,1], points[:,2])
ax.set_title("Affine plane in R^3")
plt.show()

5. Algebraic difference

• A subspace must satisfy closure under addition and scalar multiplication, and must include 0.
• An affine subspace is just a subspace plus a fixed shift vector.

Try It Yourself

1. Define a line in \(\mathbb{R}^2\):

   \[ (x,y) = (2,3) + t(1,-1) \]

   Plot it and compare with the subspace spanned by \((1,-1)\).

2. Construct an affine plane in \(\mathbb{R}^3\) shifted by vector \((5,5,5)\).

3. Show algebraically that subtracting the shift point turns an affine subspace back into a regular subspace.

The Takeaway

• Subspaces go through the origin.
• Affine subspaces are shifted copies of subspaces.
• They’re essential in geometry, computer graphics, and optimization (e.g., feasible regions in linear programming).

Chapter 5. Linear Transformation and Structure

41. Linear Transformations (Preserving Lines and Sums)

A linear transformation is a function between vector spaces that preserves two key properties:

1. Additivity: \(T(u+v) = T(u) + T(v)\)
2. Homogeneity: \(T(cu) = cT(u)\)

In practice, every linear transformation can be represented by a matrix. This lab will help you understand and experiment with linear transformations in Python.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Simple linear transformation (scaling)

Let’s scale vectors by 2 in the x-direction and by 0.5 in the y-direction.

A = np.array([
    [2, 0],
    [0, 0.5]
])

v = np.array([1, 2])
Tv = A @ v
print("Original v:", v)
print("Transformed Tv:", Tv)

Original v: [1 2]
Transformed Tv: [2. 1.]

2. Visualizing multiple vectors

vectors = [np.array([1,1]), np.array([2,0]), np.array([-1,2])]

for v in vectors:
    Tv = A @ v
    plt.arrow(0,0,v[0],v[1],head_width=0.1,color='blue',length_includes_head=True)
    plt.arrow(0,0,Tv[0],Tv[1],head_width=0.1,color='red',length_includes_head=True)

plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.xlim(-3,5)
plt.ylim(-1,5)
plt.grid()
plt.title("Blue = original, Red = transformed")
plt.show()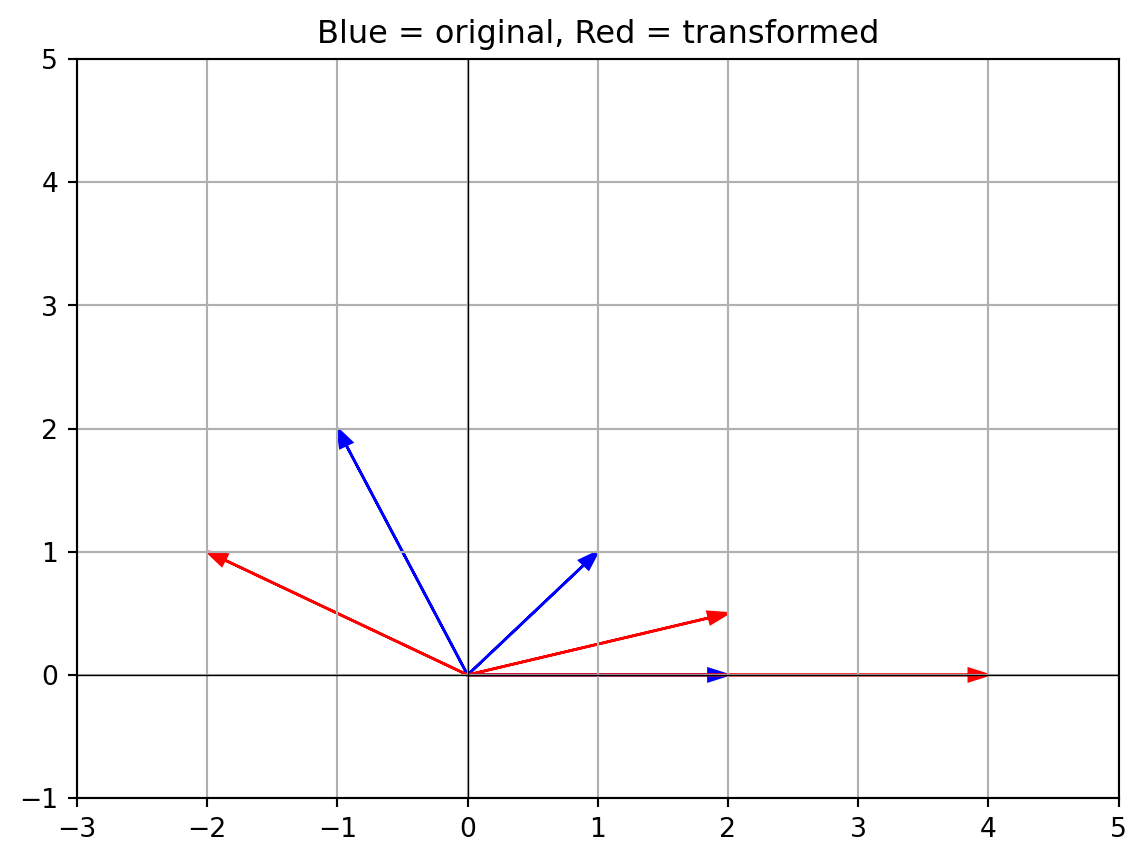

Blue arrows are the original vectors; red arrows are the transformed ones. Notice how the transformation stretches and compresses consistently.

3. Rotation as a linear transformation

Rotating vectors by \(\theta = 90^\circ\):

theta = np.pi/2
R = np.array([
    [np.cos(theta), -np.sin(theta)],
    [np.sin(theta),  np.cos(theta)]
])

v = np.array([1,0])
print("Rotate [1,0] by 90°:", R @ v)

Rotate [1,0] by 90°: [6.123234e-17 1.000000e+00]

The result is \([0,1]\), a perfect rotation.

4. Checking linearity

u = np.array([1,2])
v = np.array([3,4])
c = 5

lhs = A @ (u+v)
rhs = A@u + A@v
print("Additivity holds?", np.allclose(lhs,rhs))

lhs = A @ (c*u)
rhs = c*(A@u)
print("Homogeneity holds?", np.allclose(lhs,rhs))

Additivity holds? True
Homogeneity holds? True

Both checks return True, proving \(T\) is linear.

5. Non-linear example (for contrast)

A transformation like \(T(x,y) = (x^2, y)\) is not linear.

def nonlinear(v):
    return np.array([v[0]**2, v[1]])

print("T([2,3]) =", nonlinear(np.array([2,3])))
print("Check additivity:", nonlinear(np.array([1,2])+np.array([3,4])) == (nonlinear([1,2])+nonlinear([3,4])))

T([2,3]) = [4 3]
Check additivity: [False  True]

This fails the additivity test, so it’s not linear.

Try It Yourself

1. Define a shear matrix

   \[ S = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \]

   Apply it to vectors and plot before/after.

2. Verify linearity for rotation by 45°.

3. Test whether \(T(x,y) = (x+y, y)\) is linear.

The Takeaway

• A linear transformation preserves vector addition and scalar multiplication.
• Every linear transformation can be represented by a matrix.
• Visualizing with arrows helps build geometric intuition: stretching, rotating, and shearing are all linear.

42. Matrix Representation of a Linear Map (Choosing a Basis)

Every linear transformation can be written as a matrix, but the exact matrix depends on the basis you choose. This lab shows how to build and interpret matrix representations.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. From transformation to matrix

Suppose \(T: \mathbb{R}^2 \to \mathbb{R}^2\) is defined by:

\[ T(x,y) = (2x + y, \; x - y) \]

To find its matrix in the standard basis, apply \(T\) to each basis vector:

e1 = Matrix([1,0])
e2 = Matrix([0,1])

def T(v):
    x, y = v
    return Matrix([2*x + y, x - y])

print("T(e1):", T(e1))
print("T(e2):", T(e2))

T(e1): Matrix([[2], [1]])
T(e2): Matrix([[1], [-1]])

Stacking results as columns gives the matrix:

A = Matrix.hstack(T(e1), T(e2))
print("Matrix representation in standard basis:\n", A)

Matrix representation in standard basis:
 Matrix([[2, 1], [1, -1]])

2. Using the matrix for computations

v = Matrix([3,4])
print("T(v) via definition:", T(v))
print("T(v) via matrix:", A*v)

T(v) via definition: Matrix([[10], [-1]])
T(v) via matrix: Matrix([[10], [-1]])

Both methods match.

3. Matrix in a different basis

Now suppose we use basis

\[ B = \{ [1,1], [1,-1] \} \]

To represent \(T\) in this basis:

1. Build the change-of-basis matrix \(P\).
2. Compute \(A_B = P^{-1}AP\).

B = Matrix.hstack(Matrix([1,1]), Matrix([1,-1]))
P = B
A_B = P.inv() * A * P
print("Matrix representation in new basis:\n", A_B)

Matrix representation in new basis:
 Matrix([[3/2, 3/2], [3/2, -1/2]])

4. Interpretation

• In standard basis, \(A\) tells us how \(T\) acts on unit vectors.
• In basis \(B\), \(A_B\) shows how \(T\) looks when described using different coordinates.

5. Random linear map in \(\mathbb{R}^3\)

np.random.seed(1)
A3 = Matrix(np.random.randint(-3,4,(3,3)))
print("Random transformation matrix:\n", A3)

B3 = Matrix.hstack(Matrix([1,0,1]), Matrix([0,1,1]), Matrix([1,1,0]))
A3_B = B3.inv() * A3 * B3
print("Representation in new basis:\n", A3_B)

Random transformation matrix:
 Matrix([[2, 0, 1], [-3, -2, 0], [2, -3, -3]])
Representation in new basis:
 Matrix([[5/2, -3/2, 3], [-7/2, -9/2, -4], [1/2, 5/2, -1]])

Try It Yourself

1. Define \(T(x,y) = (x+2y, 3x+y)\). Find its matrix in the standard basis.
2. Use a new basis \(\{[2,0],[0,3]\}\). Compute the representation \(A_B\).
3. Verify that applying \(T\) directly to a vector matches computing via \(A_B\) and change-of-basis.

The Takeaway

• A linear transformation becomes a matrix representation once a basis is chosen.
• Columns of the matrix = images of basis vectors.
• Changing the basis changes the matrix, but the transformation itself stays the same.

43. Kernel and Image (Inputs That Vanish; Outputs We Can Reach)

Two fundamental subspaces describe any linear transformation \(T(x) = Ax\):

• Kernel (null space): all vectors \(x\) such that \(Ax = 0\).
• Image (column space): all possible outputs \(Ax\).

The kernel tells us what inputs collapse to zero, while the image tells us what outputs are achievable.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Kernel of a matrix

Consider

\[ A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \end{bmatrix} \]

A = Matrix([
    [1,2,3],
    [2,4,6]
])

print("Null space (kernel):", A.nullspace())

Null space (kernel): [Matrix([
[-2],
[ 1],
[ 0]]), Matrix([
[-3],
[ 0],
[ 1]])]

The null space basis shows dependencies among columns. Here, the kernel is 2-dimensional because columns are dependent.

2. Image (column space)

print("Column space (image):", A.columnspace())
print("Rank (dimension of image):", A.rank())

Column space (image): [Matrix([
[1],
[2]])]
Rank (dimension of image): 1

The image is spanned by \([1,2]^T\). So all outputs of \(A\) are multiples of this vector.

3. Interpretation

• Kernel vectors → directions that map to zero.
• Image vectors → directions we can actually reach in the output space.

If \(x \in \ker(A)\), then \(Ax = 0\). If \(b\) is not in the image, the system \(Ax = b\) has no solution.

4. Example with full rank

B = Matrix([
    [1,0,0],
    [0,1,0],
    [0,0,1]
])

print("Kernel of B:", B.nullspace())
print("Image of B:", B.columnspace())

Kernel of B: []
Image of B: [Matrix([
[1],
[0],
[0]]), Matrix([
[0],
[1],
[0]]), Matrix([
[0],
[0],
[1]])]

• Kernel = only zero vector.
• Image = all of \(\mathbb{R}^3\).

5. NumPy version (image via column space)

A = np.array([[1,2,3],[2,4,6]], dtype=float)
rank = np.linalg.matrix_rank(A)
print("Rank with NumPy:", rank)

Rank with NumPy: 1

NumPy doesn’t compute null spaces directly, but we can use SVD for that if needed.

Try It Yourself

1. Compute kernel and image for

   \[ \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \]

   What do they look like?

2. Take a random 3×4 matrix and find its kernel and image dimensions.

3. Solve \(Ax = b\) for a matrix \(A\). Try two different \(b\): one inside the image, one outside. Observe the difference.

The Takeaway

• Kernel = inputs that vanish under \(A\).
• Image = outputs that can be reached by \(A\).
• Together, they fully describe what a linear map does: what it “kills” and what it “produces.”

44. Invertibility and Isomorphisms (Perfectly Reversible Maps)

A matrix (or linear map) is invertible if it has an inverse \(A^{-1}\) such that

\[ A^{-1}A = I \quad \text{and} \quad AA^{-1} = I \]

An invertible map is also called an isomorphism, because it preserves all information - every input has exactly one output, and every output comes from exactly one input.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Checking invertibility

A = Matrix([
    [2,1],
    [5,3]
])

print("Determinant:", A.det())
print("Is invertible?", A.det() != 0)

Determinant: 1
Is invertible? True

If determinant ≠ 0 → invertible.

2. Computing the inverse

A_inv = A.inv()
print("Inverse matrix:\n", A_inv)

print("Check A*A_inv = I:\n", A * A_inv)

Inverse matrix:
 Matrix([[3, -1], [-5, 2]])
Check A*A_inv = I:
 Matrix([[1, 0], [0, 1]])

3. Solving systems with inverses

For \(Ax = b\), if \(A\) is invertible:

b = Matrix([1,2])
x = A_inv * b
print("Solution x:", x)

Solution x: Matrix([[1], [-1]])

This is equivalent to A.solve(b) in SymPy or np.linalg.solve in NumPy.

4. Non-invertible (singular) example

B = Matrix([
    [1,2],
    [2,4]
])

print("Determinant:", B.det())
print("Is invertible?", B.det() != 0)

Determinant: 0
Is invertible? False

Determinant = 0 → no inverse. The matrix collapses space onto a line, losing information.

5. NumPy version

A = np.array([[2,1],[5,3]], dtype=float)
print("Determinant:", np.linalg.det(A))
print("Inverse:\n", np.linalg.inv(A))

Determinant: 1.0000000000000002
Inverse:
 [[ 3. -1.]
 [-5.  2.]]

6. Geometric intuition

• Invertible transformation = reversible (like rotating, scaling by nonzero).
• Non-invertible transformation = squashing space into a lower dimension (like flattening a plane onto a line).

Try It Yourself

1. Test whether

   \[ \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]

   is invertible and find its inverse.

2. Compute the determinant of a 3×3 random integer matrix. If it’s nonzero, find its inverse.

3. Create a singular 3×3 matrix (make one row a multiple of another). Confirm it has no inverse.

The Takeaway

• Invertible matrix ↔︎ isomorphism: perfectly reversible, no information lost.
• Determinant ≠ 0 → invertible; determinant = 0 → singular.
• Inverses are useful conceptually, but in computation we usually solve systems directly instead of calculating \(A^{-1}\).

45. Composition, Powers, and Iteration (Doing It Again and Again)

Linear transformations can be chained together. Applying one after another is called composition, and in matrix form this becomes multiplication. Repeated application of the same transformation leads to powers of a matrix.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Composition of transformations

Suppose we have two linear maps:

• \(T_1\): rotate by 90°
• \(T_2\): scale x by 2

theta = np.pi/2
R = np.array([
    [np.cos(theta), -np.sin(theta)],
    [np.sin(theta),  np.cos(theta)]
])
S = np.array([
    [2,0],
    [0,1]
])

# Compose: apply R then S
C = S @ R
print("Composite matrix:\n", C)

Composite matrix:
 [[ 1.2246468e-16 -2.0000000e+00]
 [ 1.0000000e+00  6.1232340e-17]]

Applying the composite matrix is equivalent to applying both maps in sequence.

2. Verifying with a vector

v = np.array([1,1])
step1 = R @ v
step2 = S @ step1
composite = C @ v

print("Step-by-step:", step2)
print("Composite:", composite)

Step-by-step: [-2.  1.]
Composite: [-2.  1.]

Both results are the same → composition = matrix multiplication.

3. Powers of a matrix

Repeatedly applying a transformation corresponds to matrix powers.

Example: scaling by 2.

A = np.array([[2,0],[0,2]])
v = np.array([1,1])

print("A @ v =", A @ v)
print("A^2 @ v =", np.linalg.matrix_power(A,2) @ v)
print("A^5 @ v =", np.linalg.matrix_power(A,5) @ v)

A @ v = [2 2]
A^2 @ v = [4 4]
A^5 @ v = [32 32]

Each step doubles the scaling effect.

4. Iteration dynamics

Let’s iterate a transformation many times and see what happens.

Example:

\[ A = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \]

A = np.array([[0.5,0],[0,0.5]])
v = np.array([4,4])

for i in range(5):
    v = A @ v
    print(f"Step {i+1}:", v)

Step 1: [2. 2.]
Step 2: [1. 1.]
Step 3: [0.5 0.5]
Step 4: [0.25 0.25]
Step 5: [0.125 0.125]

Each step shrinks the vector → iteration can reveal stability.

5. Random example

np.random.seed(0)
M = np.random.randint(-2,3,(2,2))
print("Random matrix:\n", M)

print("M^2:\n", np.linalg.matrix_power(M,2))
print("M^3:\n", np.linalg.matrix_power(M,3))

Random matrix:
 [[ 2 -2]
 [ 1  1]]
M^2:
 [[ 2 -6]
 [ 3 -1]]
M^3:
 [[ -2 -10]
 [  5  -7]]

Try It Yourself

1. Create two transformations: reflection across x-axis and scaling by 3. Compose them.
2. Take a shear matrix and compute \(A^5\). What happens to a vector after repeated application?
3. Experiment with a rotation matrix raised to higher powers. What cycle do you see?

The Takeaway

• Composition of linear maps = matrix multiplication.
• Powers of a matrix represent repeated application.
• Iteration reveals long-term dynamics: shrinking, growing, or oscillating behavior.

46. Similarity and Conjugation (Same Action, Different Basis)

Two matrices \(A\) and \(B\) are called similar if there exists an invertible matrix \(P\) such that

\[ B = P^{-1} A P \]

This means \(A\) and \(B\) represent the same linear transformation, but in different bases. This lab explores similarity and why it matters.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Example with a change of basis

A = Matrix([
    [2,1],
    [0,2]
])

P = Matrix([
    [1,1],
    [0,1]
])

B = P.inv() * A * P
print("Original A:\n", A)
print("Similar matrix B:\n", B)

Original A:
 Matrix([[2, 1], [0, 2]])
Similar matrix B:
 Matrix([[2, 1], [0, 2]])

Here, \(A\) and \(B\) are similar: they describe the same transformation in different coordinates.

2. Eigenvalues stay the same

Similarity preserves eigenvalues.

print("Eigenvalues of A:", A.eigenvals())
print("Eigenvalues of B:", B.eigenvals())

Eigenvalues of A: {2: 2}
Eigenvalues of B: {2: 2}

Both matrices have the same eigenvalues, even though their entries differ.

3. Similarity and diagonalization

If a matrix is diagonalizable, there exists \(P\) such that

\[ D = P^{-1} A P \]

where \(D\) is diagonal.

C = Matrix([
    [4,1],
    [0,2]
])

P, D = C.diagonalize()
print("Diagonal form D:\n", D)
print("Check similarity (P^-1 C P = D):\n", P.inv()*C*P)

Diagonal form D:
 Matrix([[2, 0], [0, 4]])
Check similarity (P^-1 C P = D):
 Matrix([[2, 0], [0, 4]])

Diagonalization is a special case of similarity, where the new matrix is as simple as possible.

4. NumPy version

A = np.array([[2,1],[0,2]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A)
print("Eigenvalues:", eigvals)
print("Eigenvectors (basis P):\n", eigvecs)

Eigenvalues: [2. 2.]
Eigenvectors (basis P):
 [[ 1.0000000e+00 -1.0000000e+00]
 [ 0.0000000e+00  4.4408921e-16]]

Here, eigenvectors form the change-of-basis matrix \(P\).

5. Geometric interpretation

• Similar matrices = same transformation, different “ruler” (basis).
• Diagonalization = finding a ruler that makes the transformation look like pure stretching along axes.

Try It Yourself

1. Take

   \[ A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \]

   and find a matrix \(P\) that gives a similar \(B\).

2. Show that two similar matrices have the same determinant and trace.

3. For a random 3×3 matrix, check if it is diagonalizable using SymPy’s .diagonalize() method.

The Takeaway

• Similarity = same linear map, different basis.
• Similar matrices share eigenvalues, determinant, and trace.
• Diagonalization is the simplest similarity form, making repeated computations (like powers) much easier.

47. Projections and Reflections (Idempotent and Involutive Maps)

Two very common geometric linear maps are projections and reflections. They show up in graphics, physics, and optimization.

• A projection squashes vectors onto a subspace (like dropping a shadow).
• A reflection flips vectors across a line or plane (like a mirror).

Set Up Your Lab

import numpy as np
from sympy import Matrix
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Projection onto a line

If we want to project onto the line spanned by \(u\), the projection matrix is:

\[ P = \frac{uu^T}{u^T u} \]

u = np.array([2,1], dtype=float)
u = u / np.linalg.norm(u)   # normalize
P = np.outer(u,u)

print("Projection matrix:\n", P)

Projection matrix:
 [[0.8 0.4]
 [0.4 0.2]]

Apply projection:

v = np.array([3,4], dtype=float)
proj_v = P @ v
print("Original v:", v)
print("Projection of v onto u:", proj_v)

Original v: [3. 4.]
Projection of v onto u: [4. 2.]

2. Visualization of projection

plt.arrow(0,0,v[0],v[1],head_width=0.1,color="blue",length_includes_head=True)
plt.arrow(0,0,proj_v[0],proj_v[1],head_width=0.1,color="red",length_includes_head=True)
plt.arrow(proj_v[0],proj_v[1],v[0]-proj_v[0],v[1]-proj_v[1],head_width=0.1,color="gray",linestyle="dashed")

plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.title("Blue = original, Red = projection, Gray = error vector")
plt.show()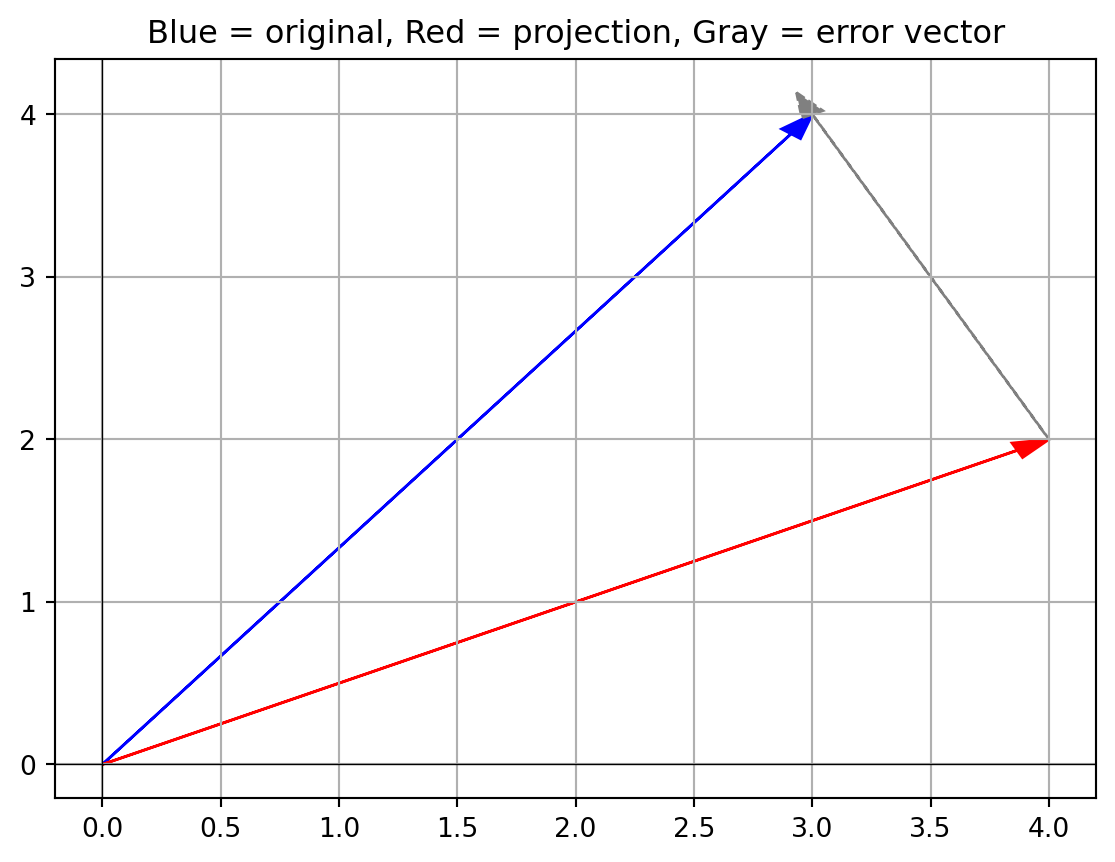

The projection is the closest point on the line to the original vector.

3. Reflection across a line

The reflection matrix across the line spanned by \(u\) is:

\[ R = 2P - I \]

I = np.eye(2)
R = 2*P - I

reflect_v = R @ v
print("Reflection of v across line u:", reflect_v)

Reflection of v across line u: [ 5.0000000e+00 -4.4408921e-16]

4. Checking algebraic properties

• Projection: \(P^2 = P\) (idempotent).
• Reflection: \(R^2 = I\) (involutive).

print("P^2 =\n", P @ P)
print("R^2 =\n", R @ R)

P^2 =
 [[0.8 0.4]
 [0.4 0.2]]
R^2 =
 [[ 1.00000000e+00 -1.59872116e-16]
 [-1.59872116e-16  1.00000000e+00]]

5. Projection in higher dimensions

Project onto the plane spanned by two vectors in \(\mathbb{R}^3\).

u1 = np.array([1,0,0], dtype=float)
u2 = np.array([0,1,0], dtype=float)

U = np.column_stack((u1,u2))   # basis for plane
P_plane = U @ np.linalg.inv(U.T @ U) @ U.T

v = np.array([1,2,3], dtype=float)
proj_plane = P_plane @ v
print("Projection onto xy-plane:", proj_plane)

Projection onto xy-plane: [1. 2. 0.]

Try It Yourself

1. Project \([4,5]\) onto the x-axis and verify the result.
2. Reflect \([1,2]\) across the line \(y=x\).
3. Create a random 3D vector and project it onto the plane spanned by \([1,1,0]\) and \([0,1,1]\).

The Takeaway

• Projection: idempotent (\(P^2 = P\)), finds the closest vector in a subspace.
• Reflection: involutive (\(R^2 = I\)), flips across a line/plane but preserves lengths.
• Both are simple but powerful examples of linear transformations with clear geometry.

48. Rotations and Shear (Geometric Intuition)

Two transformations often used in geometry, graphics, and physics are rotations and shears. Both are linear maps, but they behave differently:

• Rotation preserves lengths and angles.
• Shear preserves area (in 2D) but distorts shapes, turning squares into parallelograms.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Rotation in 2D

The rotation matrix by angle \(\theta\) is:

\[ R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \]

def rotation_matrix(theta):
    return np.array([
        [np.cos(theta), -np.sin(theta)],
        [np.sin(theta),  np.cos(theta)]
    ])

theta = np.pi/4   # 45 degrees
R = rotation_matrix(theta)

v = np.array([2,1])
rotated_v = R @ v
print("Original v:", v)
print("Rotated v (45°):", rotated_v)

Original v: [2 1]
Rotated v (45°): [0.70710678 2.12132034]

2. Visualizing rotation

plt.arrow(0,0,v[0],v[1],head_width=0.1,color="blue",length_includes_head=True)
plt.arrow(0,0,rotated_v[0],rotated_v[1],head_width=0.1,color="red",length_includes_head=True)

plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.title("Blue = original, Red = rotated (45°)")
plt.axis("equal")
plt.show()

The vector rotates counterclockwise by 45°.

3. Shear in 2D

A shear along the x-axis by factor \(k\):

\[ S = \begin{bmatrix} 1 & k \\ 0 & 1 \end{bmatrix} \]

k = 1.0
S = np.array([
    [1,k],
    [0,1]
])

sheared_v = S @ v
print("Sheared v:", sheared_v)

Sheared v: [3. 1.]

4. Visualizing shear

plt.arrow(0,0,v[0],v[1],head_width=0.1,color="blue",length_includes_head=True)
plt.arrow(0,0,sheared_v[0],sheared_v[1],head_width=0.1,color="green",length_includes_head=True)

plt.axhline(0,color='black',linewidth=0.5)
plt.axvline(0,color='black',linewidth=0.5)
plt.grid()
plt.title("Blue = original, Green = sheared")
plt.axis("equal")
plt.show()

The shear moves the vector sideways, distorting its angle.

5. Properties check

• Rotation preserves length:

print("||v|| =", np.linalg.norm(v))
print("||R v|| =", np.linalg.norm(rotated_v))

||v|| = 2.23606797749979
||R v|| = 2.2360679774997894

• Shear preserves area (determinant = 1):

print("det(S) =", np.linalg.det(S))

det(S) = 1.0

Try It Yourself

1. Rotate \([1,0]\) by 90° and check it becomes \([0,1]\).
2. Apply shear with \(k=2\) to a square (points \((0,0),(1,0),(1,1),(0,1)\)) and plot before/after.
3. Combine rotation and shear: apply shear first, then rotation. What happens?

The Takeaway

• Rotation: length- and angle-preserving, determinant = 1.
• Shear: shape-distorting but area-preserving, determinant = 1.
• Both are linear maps that provide geometric intuition and real-world modeling tools.

49. Rank and Operator Viewpoint (Rank Beyond Elimination)

The rank of a matrix tells us how much “information” a linear map carries. Algebraically, it is the dimension of the image (column space). Geometrically, it measures how many independent directions survive the transformation.

From the operator viewpoint:

• A matrix \(A\) is not just a table of numbers - it is a linear operator that maps vectors to other vectors.
• The rank is the dimension of the output space that \(A\) actually reaches.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Rank via elimination (SymPy)

A = Matrix([
    [1,2,3],
    [2,4,6],
    [1,1,1]
])

print("Matrix A:\n", A)
print("Rank of A:", A.rank())

Matrix A:
 Matrix([[1, 2, 3], [2, 4, 6], [1, 1, 1]])
Rank of A: 2

Here, the second row is a multiple of the first → less independence → rank < 3.

2. Rank via NumPy

A_np = np.array([[1,2,3],[2,4,6],[1,1,1]], dtype=float)
print("Rank (NumPy):", np.linalg.matrix_rank(A_np))

Rank (NumPy): 2

3. Operator viewpoint

Let’s apply \(A\) to random vectors:

for v in [np.array([1,0,0]), np.array([0,1,0]), np.array([0,0,1])]:
    print("A @", v, "=", A_np @ v)

A @ [1 0 0] = [1. 2. 1.]
A @ [0 1 0] = [2. 4. 1.]
A @ [0 0 1] = [3. 6. 1.]

Even though we started in 3D, all outputs lie in a plane in \(\mathbb{R}^3\). That’s why rank = 2.

4. Full rank vs reduced rank

• Full rank: the transformation preserves dimension (no collapse).
• Reduced rank: the transformation collapses onto a lower-dimensional subspace.

Example full-rank:

B = Matrix([
    [1,0,0],
    [0,1,0],
    [0,0,1]
])

print("Rank of B:", B.rank())

Rank of B: 3

5. Connection to nullity

The rank-nullity theorem:

\[ \text{rank}(A) + \text{nullity}(A) = \text{number of columns of } A \]

Check with SymPy:

print("Null space (basis):", A.nullspace())
print("Nullity:", len(A.nullspace()))
print("Rank + Nullity =", A.rank() + len(A.nullspace()))

Null space (basis): [Matrix([
[ 1],
[-2],
[ 1]])]
Nullity: 1
Rank + Nullity = 3

Try It Yourself

1. Take

   \[ \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \]

   and compute its rank. Why is it 1?

2. For a random 4×4 matrix, use np.linalg.matrix_rank to check if it’s invertible.

3. Verify rank-nullity theorem for a 3×5 random integer matrix.

The Takeaway

• Rank = dimension of the image (how many independent outputs a transformation has).
• Operator viewpoint: rank shows how much of the input space survives after transformation.
• Rank-nullity links the image and kernel - together they fully describe a linear operator.

50. Block Matrices and Block Maps (Divide and Conquer Structure)

Sometimes matrices can be arranged in blocks (submatrices). Treating a big matrix as smaller pieces helps simplify calculations, especially in systems with structure (networks, coupled equations, or partitioned variables).

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Constructing block matrices

We can build a block matrix from smaller pieces:

A11 = Matrix([[1,2],[3,4]])
A12 = Matrix([[5,6],[7,8]])
A21 = Matrix([[9,10]])
A22 = Matrix([[11,12]])

# Combine into a block matrix
A = Matrix.vstack(
    Matrix.hstack(A11, A12),
    Matrix.hstack(A21, A22)
)
print("Block matrix A:\n", A)

Block matrix A:
 Matrix([[1, 2, 5, 6], [3, 4, 7, 8], [9, 10, 11, 12]])

2. Block multiplication

If a matrix is partitioned into blocks, multiplication follows block rules:

\[ \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} Ax + By \\ Cx + Dy \end{bmatrix} \]

Example:

A = Matrix([
    [1,2,5,6],
    [3,4,7,8],
    [9,10,11,12]
])

x = Matrix([1,1,2,2])
print("A * x =", A*x)

A * x = Matrix([[25], [37], [65]])

Here the vector is split into blocks \([x,y]\).

3. Block diagonal matrices

Block diagonal = independent subproblems:

B1 = Matrix([[2,0],[0,2]])
B2 = Matrix([[3,1],[0,3]])

BlockDiag = Matrix([
    [2,0,0,0],
    [0,2,0,0],
    [0,0,3,1],
    [0,0,0,3]
])

print("Block diagonal matrix:\n", BlockDiag)

Block diagonal matrix:
 Matrix([[2, 0, 0, 0], [0, 2, 0, 0], [0, 0, 3, 1], [0, 0, 0, 3]])

Applying this matrix acts separately on each block - like running two smaller transformations in parallel.

4. Inverse of block diagonal

The inverse of a block diagonal is just the block diagonal of inverses:

B1_inv = B1.inv()
B2_inv = B2.inv()
BlockDiagInv = Matrix([
    [B1_inv[0,0],0,0,0],
    [0,B1_inv[1,1],0,0],
    [0,0,B2_inv[0,0],B2_inv[0,1]],
    [0,0,B2_inv[1,0],B2_inv[1,1]]
])
print("Inverse block diag:\n", BlockDiagInv)

Inverse block diag:
 Matrix([[1/2, 0, 0, 0], [0, 1/2, 0, 0], [0, 0, 1/3, -1/9], [0, 0, 0, 1/3]])

5. Practical example - coupled equations

Suppose we have two independent systems:

• System 1: \(Ax = b\)
• System 2: \(Cy = d\)

We can represent both together:

\[ \begin{bmatrix} A & 0 \\ 0 & C \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} b \\ d \end{bmatrix} \]

This shows how block matrices organize multiple systems in one big equation.

Try It Yourself

1. Build a block diagonal matrix with three 2×2 blocks. Apply it to a vector.
2. Verify block multiplication rule by manually computing \(Ax + By\) and \(Cx + Dy\).
3. Write two small systems of equations and combine them into one block system.

The Takeaway

• Block matrices let us break down big systems into smaller parts.
• Block diagonal matrices = independent subsystems.
• Thinking in blocks simplifies algebra, programming, and numerical computation.

Chapter 6. Determinants and volume

51. Areas, Volumes, and Signed Scale Factors (Geometric Entry Point)

The determinant of a matrix has a deep geometric meaning: it tells us how a linear transformation scales area (in 2D), volume (in 3D), or higher-dimensional content. It can also flip orientation (sign).

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Determinant in 2D (area scaling)

Let’s take a matrix that stretches and shears:

A = Matrix([
    [2,1],
    [1,1]
])

print("Determinant:", A.det())

Determinant: 1

The determinant = 1 → areas are preserved, even though the shape is distorted.

2. Unit square under transformation

Transform the square with corners \((0,0),(1,0),(1,1),(0,1)\):

square = Matrix([
    [0,0],
    [1,0],
    [1,1],
    [0,1]
])

transformed = (A * square.T).T
print("Original square:\n", square)
print("Transformed square:\n", transformed)

Original square:
 Matrix([[0, 0], [1, 0], [1, 1], [0, 1]])
Transformed square:
 Matrix([[0, 0], [2, 1], [3, 2], [1, 1]])

The area of the transformed shape equals \(|\det(A)|\).

3. Determinant in 3D (volume scaling)

B = Matrix([
    [1,2,0],
    [0,1,0],
    [0,0,3]
])

print("Determinant:", B.det())

Determinant: 3

\(\det(B)=3\) means that volumes are scaled by 3.

4. Negative determinant = orientation flip

C = Matrix([
    [0,1],
    [1,0]
])

print("Determinant:", C.det())

Determinant: -1

The determinant = -1 → area preserved but orientation flipped (like a mirror reflection).

5. NumPy version

A = np.array([[2,1],[1,1]], dtype=float)
print("Det (NumPy):", np.linalg.det(A))

Det (NumPy): 1.0

Try It Yourself

1. Take

   \[ \begin{bmatrix} 3 & 0 \\ 0 & 2 \end{bmatrix} \]

   and compute the determinant. Verify it scales areas by 6.

2. Build a 3×3 shear matrix and check how it affects volume.

3. Test a reflection matrix and confirm that the determinant is negative.

The Takeaway

• Determinant measures how a linear map scales area, volume, or hypervolume.
• Positive determinant = preserves orientation; negative = flips it.
• Magnitude of determinant = scaling factor of geometric content.

52. Determinant via Linear Rules (Multilinearity, Sign, Normalization)

The determinant isn’t just a formula; it’s defined by three elegant rules that make it unique. These rules capture its geometric meaning as a volume-scaling factor.

1. Multilinearity: Linear in each row (or column).
2. Sign Change: Swapping two rows flips the sign.
3. Normalization: The determinant of the identity matrix is 1.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Multilinearity

If one row is scaled, the determinant scales the same way.

A = Matrix([[1,2],[3,4]])
print("det(A):", A.det())

B = Matrix([[2,4],[3,4]])  # first row doubled
print("det(B):", B.det())

det(A): -2
det(B): -4

You’ll see det(B) = 2 * det(A).

2. Sign change by row swap

C = Matrix([[1,2],[3,4]])
C_swapped = Matrix([[3,4],[1,2]])

print("det(C):", C.det())
print("det(C_swapped):", C_swapped.det())

det(C): -2
det(C_swapped): 2

Swapping rows flips the sign of the determinant.

3. Normalization rule

I = Matrix.eye(3)
print("det(I):", I.det())

det(I): 1

The determinant of the identity is always 1 - this fixes the scaling baseline.

4. Combining rules (example in 3×3)

M = Matrix([[1,2,3],[4,5,6],[7,8,9]])
print("det(M):", M.det())

det(M): 0

Here, rows are linearly dependent, so the determinant is 0 - consistent with multilinearity (since one row can be written as a combo of others).

5. NumPy check

A = np.array([[1,2],[3,4]], dtype=float)
print("det(A) NumPy:", np.linalg.det(A))

det(A) NumPy: -2.0000000000000004

Both SymPy and NumPy confirm the same result.

Try It Yourself

1. Scale a row of a 3×3 matrix by 3. Confirm the determinant scales by 3.
2. Swap two rows twice in a row - does the determinant return to its original value?
3. Compute determinant of a triangular matrix. What pattern do you see?

The Takeaway

• Determinant is defined by multilinearity, sign change, and normalization.
• These rules uniquely pin down the determinant’s behavior.
• Every formula (cofactor expansion, row-reduction method, etc.) comes from these core principles.

53. Determinant and Row Operations (How Each Move Changes det)

Row operations are at the heart of Gaussian elimination, and the determinant has simple, predictable reactions to them. Understanding these reactions gives both computational shortcuts and geometric intuition.

The Three Key Rules

1. Row swap: Swapping two rows flips the sign of the determinant.
2. Row scaling: Multiplying a row by a scalar \(c\) multiplies the determinant by \(c\).
3. Row replacement: Adding a multiple of one row to another leaves the determinant unchanged.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Row swap

A = Matrix([[1,2],[3,4]])
print("det(A):", A.det())

A_swapped = Matrix([[3,4],[1,2]])
print("det(after swap):", A_swapped.det())

det(A): -2
det(after swap): 2

The result flips sign.

2. Row scaling

B = Matrix([[1,2],[3,4]])
B_scaled = Matrix([[2,4],[3,4]])  # first row × 2

print("det(B):", B.det())
print("det(after scaling row 1 by 2):", B_scaled.det())

det(B): -2
det(after scaling row 1 by 2): -4

Determinant is multiplied by 2.

3. Row replacement (no change)

C = Matrix([[1,2],[3,4]])
C_replaced = Matrix([[1,2],[3-2*1, 4-2*2]])  # row2 → row2 - 2*row1

print("det(C):", C.det())
print("det(after row replacement):", C_replaced.det())

det(C): -2
det(after row replacement): -2

Determinant stays the same.

4. Triangular form shortcut

Since elimination only uses row replacement (which doesn’t change the determinant) and row swaps/scales (which we can track), the determinant of a triangular matrix is just the product of its diagonal entries.

D = Matrix([[2,1,3],[0,4,5],[0,0,6]])
print("det(D):", D.det())
print("Product of diagonals:", 2*4*6)

det(D): 48
Product of diagonals: 48

5. NumPy confirmation

A = np.array([[1,2,3],[0,4,5],[1,0,6]], dtype=float)
print("det(A):", np.linalg.det(A))

det(A): 22.000000000000004

Try It Yourself

1. Take

   \[ \begin{bmatrix} 2 & 3 \\ 4 & 6 \end{bmatrix} \]

   and scale the second row by \(\tfrac{1}{2}\). Compare determinants before and after.

2. Do Gaussian elimination on a 3×3 matrix, and track how each row operation changes the determinant.

3. Compute determinant by reducing to triangular form and compare with SymPy’s .det().

The Takeaway

• Determinant reacts predictably to row operations.
• Row replacement is “safe” (no change), scaling multiplies by the factor, and swapping flips the sign.
• This makes elimination not just a solving tool, but also a method to compute determinants efficiently.

54. Triangular Matrices and Product of Diagonals (Fast Wins)

For triangular matrices (upper or lower), the determinant is simply the product of the diagonal entries. This rule is one of the biggest shortcuts in linear algebra - no expansion or elimination needed.

Why It Works

• Triangular matrices already look like the end result of Gaussian elimination.
• Since row replacement operations don’t change the determinant, what’s left is just the product of the diagonal.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Upper triangular example

A = Matrix([
    [2,1,3],
    [0,4,5],
    [0,0,6]
])

print("det(A):", A.det())
print("Product of diagonals:", 2*4*6)

det(A): 48
Product of diagonals: 48

Both values match exactly.

2. Lower triangular example

B = Matrix([
    [7,0,0],
    [2,5,0],
    [3,4,9]
])

print("det(B):", B.det())
print("Product of diagonals:", 7*5*9)

det(B): 315
Product of diagonals: 315

3. Diagonal matrix (special case)

For diagonal matrices, determinant = product of diagonal entries directly.

C = Matrix.diag(3,5,7)
print("det(C):", C.det())
print("Product of diagonals:", 3*5*7)

det(C): 105
Product of diagonals: 105

4. NumPy version

A = np.array([[2,1,3],[0,4,5],[0,0,6]], dtype=float)
print("det(A):", np.linalg.det(A))
print("Product of diagonals:", np.prod(np.diag(A)))

det(A): 47.999999999999986
Product of diagonals: 48.0

5. Quick elimination to triangular form

Even for non-triangular matrices, elimination reduces them to triangular form, where this rule applies.

D = Matrix([[1,2,3],[4,5,6],[7,8,10]])
print("det(D) via SymPy:", D.det())
print("det(D) via LU decomposition:", D.LUdecomposition()[0].det() * D.LUdecomposition()[1].det())

det(D) via SymPy: -3
det(D) via LU decomposition: -3

Try It Yourself

1. Compute the determinant of a 4×4 diagonal matrix quickly.
2. Verify that triangular matrices with a zero on the diagonal always have determinant 0.
3. Use SymPy to check that elimination to triangular form preserves determinant (except for swaps/scales).

The Takeaway

• For triangular (and diagonal) matrices:

  \[ \det(A) = \prod_{i} a_{ii} \]

• This shortcut makes determinant computation trivial.

• Gaussian elimination leverages this fact: once reduced to triangular form, the determinant is just the product of pivots (with sign adjustments for swaps).

55. det(AB) = det(A)det(B) (Multiplicative Magic)

One of the most elegant properties of determinants is multiplicativity:

\[ \det(AB) = \det(A)\,\det(B) \]

This rule is powerful because it connects algebra (matrix multiplication) with geometry (volume scaling).

Geometric Intuition

• If \(A\) scales volumes by factor \(\det(A)\), and \(B\) scales them by \(\det(B)\), then applying \(B\) followed by \(A\) scales volumes by \(\det(A)\det(B)\).
• This property works in all dimensions.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. 2×2 example

A = Matrix([[2,1],[0,3]])
B = Matrix([[1,4],[2,5]])

detA = A.det()
detB = B.det()
detAB = (A*B).det()

print("det(A):", detA)
print("det(B):", detB)
print("det(AB):", detAB)
print("det(A)*det(B):", detA*detB)

det(A): 6
det(B): -3
det(AB): -18
det(A)*det(B): -18

The two results match.

2. 3×3 random matrix check

np.random.seed(1)
A = Matrix(np.random.randint(-3,4,(3,3)))
B = Matrix(np.random.randint(-3,4,(3,3)))

print("det(A):", A.det())
print("det(B):", B.det())
print("det(AB):", (A*B).det())
print("det(A)*det(B):", A.det()*B.det())

det(A): 25
det(B): -15
det(AB): -375
det(A)*det(B): -375

3. Special cases

• If \(\det(A)=0\), then \(\det(AB)=0\).
• If \(\det(A)=\pm1\), it acts like a “volume-preserving” transformation (rotation/reflection).

A = Matrix([[1,0],[0,0]])  # singular
B = Matrix([[2,3],[4,5]])

print("det(A):", A.det())
print("det(AB):", (A*B).det())

det(A): 0
det(AB): 0

Both are 0.

4. NumPy version

A = np.array([[2,1],[0,3]], dtype=float)
B = np.array([[1,4],[2,5]], dtype=float)

lhs = np.linalg.det(A @ B)
rhs = np.linalg.det(A) * np.linalg.det(B)

print("det(AB) =", lhs)
print("det(A)*det(B) =", rhs)

det(AB) = -17.999999999999996
det(A)*det(B) = -17.999999999999996

Try It Yourself

1. Construct two triangular matrices and verify multiplicativity (diagonal products multiply too).
2. Test the property with an orthogonal matrix \(Q\) (\(\det(Q)=\pm 1\)). What happens?
3. Try with one matrix singular - confirm the product is always singular.

The Takeaway

• Determinant is multiplicative, not additive.
• \(\det(AB) = \det(A)\det(B)\) is a cornerstone identity in linear algebra.
• This property connects geometry (volume scaling) with algebra (matrix multiplication).

56. Invertibility and Zero Determinant (Flat vs. Full Volume)

The determinant gives a quick test for invertibility:

• If \(\det(A) \neq 0\), the matrix is invertible.
• If \(\det(A) = 0\), the matrix is singular (non-invertible).

Geometrically:

• Nonzero determinant → transformation keeps full dimension (no collapse).
• Zero determinant → transformation flattens space into a lower dimension (volume = 0).

Set Up Your Lab

import numpy as np
from sympy import Matrix
from sympy.matrices.common import NonInvertibleMatrixError

Step-by-Step Code Walkthrough

1. Invertible example

A = Matrix([[2,1],[5,3]])
print("det(A):", A.det())
print("Inverse exists?", A.det() != 0)
print("A inverse:\n", A.inv())

det(A): 1
Inverse exists? True
A inverse:
 Matrix([[3, -1], [-5, 2]])

The determinant is nonzero → invertible.

2. Singular example (zero determinant)

B = Matrix([[1,2],[2,4]])
print("det(B):", B.det())
print("Inverse exists?", B.det() != 0)

det(B): 0
Inverse exists? False

Since the second row is a multiple of the first, determinant = 0 → no inverse.

3. Solving systems with determinant check

If \(\det(A)=0\), the system \(Ax=b\) may have no solutions or infinitely many.

# 3. Solving systems with determinant check
b = Matrix([1,2])
try:
    print("Solve Ax=b with singular B:", B.solve(b))
except NonInvertibleMatrixError as e:
    print("Error when solving Ax=b:", e)

Error when solving Ax=b: Matrix det == 0; not invertible.

SymPy indicates inconsistency or multiple solutions.

4. Higher-dimensional example

C = Matrix([
    [1,0,0],
    [0,2,0],
    [0,0,3]
])
print("det(C):", C.det())
print("Invertible?", C.det() != 0)

det(C): 6
Invertible? True

Diagonal entries all nonzero → invertible.

5. NumPy version

A = np.array([[2,1],[5,3]], dtype=float)
print("det(A):", np.linalg.det(A))
print("Inverse:\n", np.linalg.inv(A))

B = np.array([[1,2],[2,4]], dtype=float)
print("det(B):", np.linalg.det(B))
# np.linalg.inv(B) would fail because det=0

det(A): 1.0000000000000002
Inverse:
 [[ 3. -1.]
 [-5.  2.]]
det(B): 0.0

Try It Yourself

1. Build a 3×3 matrix with determinant 0 by making one row a multiple of another. Confirm singularity.
2. Generate a random 4×4 matrix and check whether it’s invertible using .det().
3. Test if two different 2×2 matrices are invertible, then multiply them together - is the product invertible too?

The Takeaway

• \(\det(A) \neq 0 \implies\) invertible (full volume).
• \(\det(A) = 0 \implies\) singular (space collapsed).
• Determinant gives both algebraic and geometric insight into when a matrix is reversible.

57. Cofactor Expansion (Laplace’s Method)

The cofactor expansion is a systematic way to compute determinants using minors. It’s not efficient for large matrices, but it reveals the recursive structure of determinants.

Definition

For an \(n \times n\) matrix \(A\),

\[ \det(A) = \sum_{j=1}^{n} (-1)^{i+j} a_{ij} \det(M_{ij}) \]

where:

• \(i\) = chosen row (or column),
• \(M_{ij}\) = minor matrix after removing row \(i\), column \(j\).

Set Up Your Lab

import numpy as np
from sympy import Matrix, symbols

Step-by-Step Code Walkthrough

1. 2×2 case (base rule)

# declare symbols
a, b, c, d = symbols('a b c d')

# build the matrix
A = Matrix([[a, b],[c, d]])

# compute determinant
detA = A.det()
print("Determinant 2x2:", detA)

Determinant 2x2: a*d - b*c

Formula: \(\det(A) = ad - bc\).

2. 3×3 example using cofactor expansion

A = Matrix([
    [1,2,3],
    [4,5,6],
    [7,8,9]
])

detA = A.det()
print("Determinant via SymPy:", detA)

Determinant via SymPy: 0

Let’s compute manually along the first row:

cofactor_expansion = (
    1 * Matrix([[5,6],[8,9]]).det()
    - 2 * Matrix([[4,6],[7,9]]).det()
    + 3 * Matrix([[4,5],[7,8]]).det()
)
print("Cofactor expansion result:", cofactor_expansion)

Cofactor expansion result: 0

Both match (here = 0 because rows are dependent).

3. Expansion along different rows/columns

The result is the same no matter which row/column you expand along.

cofactor_col1 = (
    1 * Matrix([[2,3],[8,9]]).det()
    - 4 * Matrix([[2,3],[5,6]]).det()
    + 7 * Matrix([[2,3],[5,6]]).det()
)
print("Expansion along col1:", cofactor_col1)

Expansion along col1: -15

4. Larger example (4×4)

B = Matrix([
    [2,0,1,3],
    [1,2,0,4],
    [0,1,1,0],
    [3,0,2,1]
])

print("Determinant 4x4:", B.det())

Determinant 4x4: -15

SymPy handles it directly, but conceptually it’s still the same recursive expansion.

5. NumPy vs SymPy

B_np = np.array([[2,0,1,3],[1,2,0,4],[0,1,1,0],[3,0,2,1]], dtype=float)
print("NumPy determinant:", np.linalg.det(B_np))

NumPy determinant: -15.0

Try It Yourself

1. Compute a 3×3 determinant manually using cofactor expansion and confirm with .det().
2. Expand along a different row and check that the result is unchanged.
3. Build a 4×4 diagonal matrix and expand it - what simplification do you notice?

The Takeaway

• Cofactor expansion defines determinant recursively.
• Works on any row or column, with consistent results.
• Important for proofs and theory, though not practical for computation on large matrices.

58. Permutations and Sign (The Combinatorial Core)

The determinant can also be defined using permutations of indices. This looks abstract, but it’s the most fundamental definition:

\[ \det(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^n a_{i,\sigma(i)} \]

• \(S_n\) = set of all permutations of \(\{1,\dots,n\}\)
• \(\text{sgn}(\sigma)\) = +1 if the permutation is even, -1 if odd
• Each term = one product of entries, one from each row and column

This formula explains why determinants mix signs, why row swaps flip the determinant, and why dependence kills it.

Set Up Your Lab

import itertools
import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Determinant by permutation expansion (3×3)

def determinant_permutation(A):
    n = A.shape[0]
    total = 0
    for perm in itertools.permutations(range(n)):
        sign = (-1)**(sum(1 for i in range(n) for j in range(i) if perm[j] > perm[i]))
        product = 1
        for i in range(n):
            product *= A[i, perm[i]]
        total += sign * product
    return total

A = np.array([[1,2,3],
              [4,5,6],
              [7,8,9]])

print("Permutation formula det:", determinant_permutation(A))
print("NumPy det:", np.linalg.det(A))

Permutation formula det: 0
NumPy det: -9.51619735392994e-16

Both results ≈ 0, since rows are dependent.

2. Count permutations

For \(n=3\), there are \(3! = 6\) terms:

\[ \det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \]

You can see the alternating signs explicitly.

3. Verification with SymPy

M = Matrix([[2,1,0],
            [1,3,4],
            [0,2,5]])
print("SymPy det:", M.det())

SymPy det: 9

Matches the permutation expansion.

4. Growth of terms

• 2×2 → 2 terms
• 3×3 → 6 terms
• 4×4 → 24 terms
• \(n\) → \(n!\) terms (factorial growth!)

This is why cofactor or LU is preferred computationally.

Try It Yourself

1. Write out the 2×2 permutation formula explicitly and check it equals \(ad - bc\).
2. Expand a 3×3 determinant by hand using the six terms.
3. Modify the code to count how many multiplications are required for a 5×5 matrix using the permutation definition.

The Takeaway

• Determinant = signed sum over all permutations.
• Signs come from permutation parity (even/odd swaps).
• This definition is the combinatorial foundation that unifies all determinant properties.

59. Cramer’s Rule (Solving with Determinants, and When Not to Use It)

Cramer’s Rule gives an explicit formula for solving a system of linear equations \(Ax = b\) using determinants. It is elegant but inefficient for large systems.

For \(A \in \mathbb{R}^{n \times n}\) with \(\det(A) \neq 0\):

\[ x_i = \frac{\det(A_i)}{\det(A)} \]

where \(A_i\) is \(A\) with its \(i\)-th column replaced by \(b\).

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Simple 2×2 example

Solve:

\[ \begin{cases} 2x + y = 5 \\ x - y = 1 \end{cases} \]

A = Matrix([[2,1],[1,-1]])
b = Matrix([5,1])

detA = A.det()
print("det(A):", detA)

# Replace columns
A1 = A.copy()
A1[:,0] = b
A2 = A.copy()
A2[:,1] = b

x1 = A1.det() / detA
x2 = A2.det() / detA
print("Solution via Cramer's Rule:", [x1, x2])

# Check with built-in solver
print("SymPy solve:", A.LUsolve(b))

det(A): -3
Solution via Cramer's Rule: [2, 1]
SymPy solve: Matrix([[2], [1]])

Both give the same solution.

2. 3×3 example

A = Matrix([
    [1,2,3],
    [0,1,4],
    [5,6,0]
])
b = Matrix([7,8,9])

detA = A.det()
print("det(A):", detA)

solutions = []
for i in range(A.shape[1]):
    Ai = A.copy()
    Ai[:,i] = b
    solutions.append(Ai.det()/detA)

print("Solution via Cramer's Rule:", solutions)
print("SymPy solve:", A.LUsolve(b))

det(A): 1
Solution via Cramer's Rule: [21, -16, 6]
SymPy solve: Matrix([[21], [-16], [6]])

3. NumPy version (inefficient but illustrative)

A = np.array([[2,1],[1,-1]], dtype=float)
b = np.array([5,1], dtype=float)

detA = np.linalg.det(A)

solutions = []
for i in range(A.shape[1]):
    Ai = A.copy()
    Ai[:,i] = b
    solutions.append(np.linalg.det(Ai)/detA)

print("Solution:", solutions)

Solution: [np.float64(2.0000000000000004), np.float64(1.0)]

4. Why not use it in practice?

• Requires computing \(n+1\) determinants.
• Determinant computation via cofactor expansion is factorial-time.
• Gaussian elimination or LU is far more efficient.

Try It Yourself

1. Solve a 3×3 system using Cramer’s Rule and confirm with A.solve(b).
2. Try Cramer’s Rule when \(\det(A)=0\). What happens?
3. Compare runtime of Cramer’s Rule vs LU for a random 5×5 matrix.

The Takeaway

• Cramer’s Rule gives explicit formulas for solutions using determinants.
• Beautiful for theory, useful for small cases, but not computationally practical.
• It highlights the deep connection between determinants and solving linear systems.

60. Computing Determinants in Practice (Use LU, Mind Stability)

While definitions like cofactor expansion and permutations are beautiful, they are too slow for large matrices. In practice, determinants are computed using row reduction or LU decomposition, with careful attention to numerical stability.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Cofactor expansion is too slow

A = Matrix([
    [1,2,3],
    [4,5,6],
    [7,8,10]
])
print("det via cofactor expansion:", A.det())

det via cofactor expansion: -3

This works for 3×3, but complexity grows factorially.

2. Determinant via triangular form (LU decomposition)

LU decomposition factorizes \(A = LU\), where \(L\) is lower triangular and \(U\) is upper triangular. Determinant = product of diagonals of \(U\), up to sign corrections for row swaps.

L, U, perm = A.LUdecomposition()
detA = A.det()
print("L:\n", L)
print("U:\n", U)
print("Permutation matrix:\n", perm)
print("det via LU product:", detA)

L:
 Matrix([[1, 0, 0], [4, 1, 0], [7, 2, 1]])
U:
 Matrix([[1, 2, 3], [0, -3, -6], [0, 0, 1]])
Permutation matrix:
 []
det via LU product: -3

3. NumPy efficient method

A_np = np.array([[1,2,3],[4,5,6],[7,8,10]], dtype=float)
print("NumPy det:", np.linalg.det(A_np))

NumPy det: -3.000000000000001

NumPy uses optimized routines (LAPACK under the hood).

4. Large random matrix

np.random.seed(0)
B = np.random.rand(5,5)
print("NumPy det (5x5):", np.linalg.det(B))

NumPy det (5x5): 0.009658225505885114

Computes quickly even for larger matrices.

5. Stability issues

Determinants of large or ill-conditioned matrices can suffer from floating-point errors. For example, if rows are nearly dependent:

C = np.array([[1,2,3],[2,4.0000001,6],[3,6,9]], dtype=float)
print("det(C):", np.linalg.det(C))

det(C): -4.996003624823549e-23

The result may not be exactly 0 due to floating-point approximations.

Try It Yourself

1. Compute the determinant of a random 10×10 matrix with np.linalg.det.
2. Compare results between SymPy (exact rational arithmetic) and NumPy (floating-point).
3. Test determinant of a nearly singular matrix - notice numerical instability.

The Takeaway

• Determinants in practice are computed with LU decomposition or equivalent.
• Always be mindful of numerical stability - small errors matter when determinant ≈ 0.
• For exact answers (small cases), use symbolic tools like SymPy; for speed, use NumPy.

Chapter 7. Eigenvalues, Eigenvectors, and Dynamics

61. Eigenvalues and Eigenvectors (Directions That Stay Put)

An eigenvector of a matrix \(A\) is a special vector that doesn’t change direction when multiplied by \(A\). Instead, it only gets stretched or shrunk by a scalar called the eigenvalue.

Formally:

\[ A v = \lambda v \]

where \(v\) is an eigenvector and \(\lambda\) is the eigenvalue.

Geometrically: eigenvectors are “preferred directions” of a linear transformation.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. A simple 2×2 example

A = Matrix([
    [2,1],
    [1,2]
])

eigs = A.eigenvects()
print("Eigenvalues and eigenvectors:", eigs)

Eigenvalues and eigenvectors: [(1, 1, [Matrix([
[-1],
[ 1]])]), (3, 1, [Matrix([
[1],
[1]])])]

This outputs eigenvalues and their associated eigenvectors.

2. Verify the eigen equation

Pick one eigenpair \((\lambda, v)\):

lam = eigs[0][0]
v = eigs[0][2][0]
print("Check Av = λv:", A*v, lam*v)

Check Av = λv: Matrix([[-1], [1]]) Matrix([[-1], [1]])

Both sides match → confirming the eigenpair.

3. NumPy version

A_np = np.array([[2,1],[1,2]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A_np)

print("Eigenvalues:", eigvals)
print("Eigenvectors:\n", eigvecs)

Eigenvalues: [3. 1.]
Eigenvectors:
 [[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

Columns of eigvecs are eigenvectors.

4. Geometric interpretation (plot)

import matplotlib.pyplot as plt

v1 = np.array(eigvecs[:,0])
v2 = np.array(eigvecs[:,1])

plt.arrow(0,0,v1[0],v1[1],head_width=0.1,color="blue",length_includes_head=True)
plt.arrow(0,0,v2[0],v2[1],head_width=0.1,color="red",length_includes_head=True)

plt.axhline(0,color="black",linewidth=0.5)
plt.axvline(0,color="black",linewidth=0.5)
plt.axis("equal")
plt.grid()
plt.title("Eigenvectors: directions that stay put")
plt.show()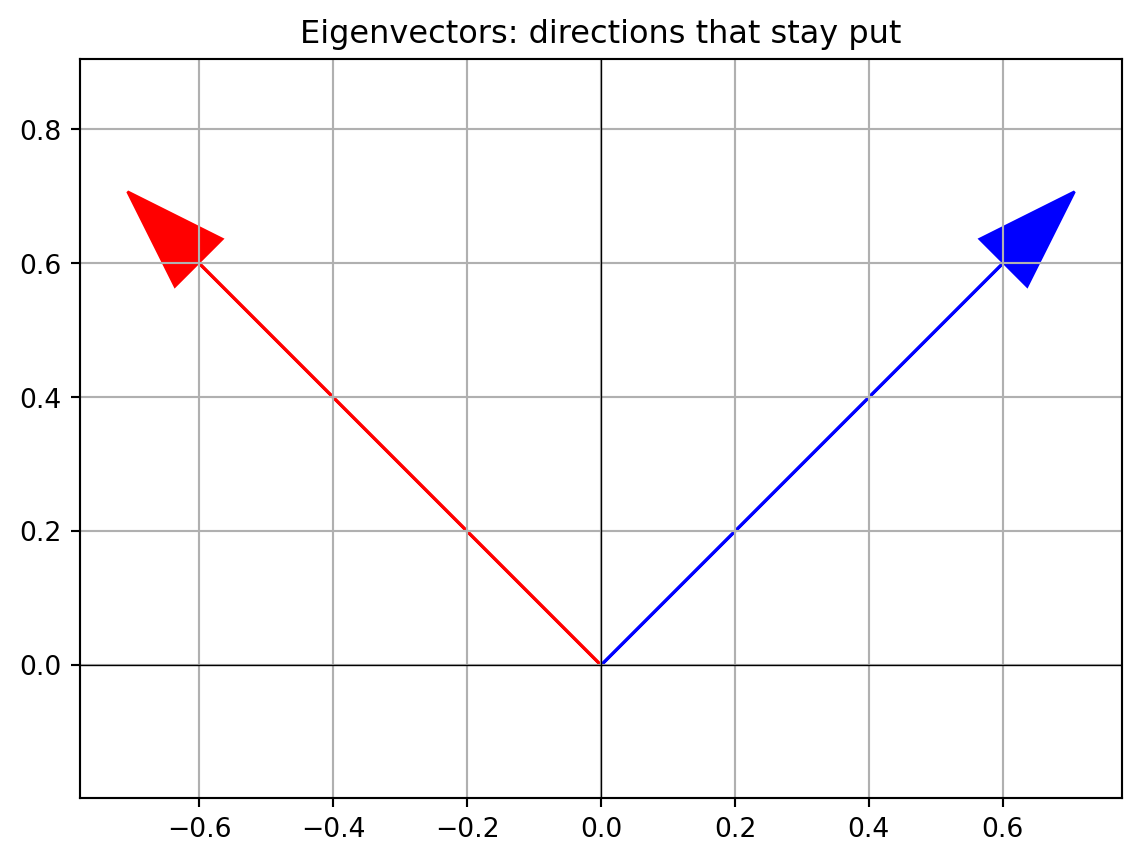

Both eigenvectors define directions where the transformation acts by scaling only.

5. Random 3×3 matrix example

np.random.seed(1)
B = Matrix(np.random.randint(-2,3,(3,3)))
print("Matrix B:\n", B)
print("Eigenvalues/vectors:", B.eigenvects())

Matrix B:
 Matrix([[1, 2, -2], [-1, 1, -2], [-2, -1, 2]])
Eigenvalues/vectors: [(4/3 + (-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3) + 13/(9*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)), 1, [Matrix([
[ -16/27 - 91/(81*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)) + (4/3 + (-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3) + 13/(9*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)))**2/9 - 7*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)/9],
[50/27 + 5*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)/9 - 2*(4/3 + (-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3) + 13/(9*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)))**2/9 + 65/(81*(-1/2 - sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3))],
[                                                                                                                                                                                                                                                              1]])]), (4/3 + 13/(9*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)) + (-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3), 1, [Matrix([
[ -16/27 - 7*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)/9 + (4/3 + 13/(9*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)) + (-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3))**2/9 - 91/(81*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3))],
[50/27 + 65/(81*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)) - 2*(4/3 + 13/(9*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)) + (-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3))**2/9 + 5*(-1/2 + sqrt(3)*I/2)*(2*sqrt(43)/3 + 127/27)**(1/3)/9],
[                                                                                                                                                                                                                                                              1]])]), (13/(9*(2*sqrt(43)/3 + 127/27)**(1/3)) + 4/3 + (2*sqrt(43)/3 + 127/27)**(1/3), 1, [Matrix([
[  -7*(2*sqrt(43)/3 + 127/27)**(1/3)/9 - 16/27 - 91/(81*(2*sqrt(43)/3 + 127/27)**(1/3)) + (13/(9*(2*sqrt(43)/3 + 127/27)**(1/3)) + 4/3 + (2*sqrt(43)/3 + 127/27)**(1/3))**2/9],
[-2*(13/(9*(2*sqrt(43)/3 + 127/27)**(1/3)) + 4/3 + (2*sqrt(43)/3 + 127/27)**(1/3))**2/9 + 65/(81*(2*sqrt(43)/3 + 127/27)**(1/3)) + 5*(2*sqrt(43)/3 + 127/27)**(1/3)/9 + 50/27],
[                                                                                                                                                                           1]])])]

Try It Yourself

1. Compute eigenvalues and eigenvectors of

   \[ \begin{bmatrix} 3 & 0 \\ 0 & 2 \end{bmatrix} \]

   and verify that they match the diagonal entries.

2. Use NumPy to find eigenvectors of a rotation matrix by 90°. What do you notice?

3. For a singular matrix, check if 0 is an eigenvalue.

The Takeaway

• Eigenvalues = scale factors; eigenvectors = directions that stay put.
• The eigen equation \(Av=\lambda v\) captures the essence of a matrix’s action.
• They form the foundation for deeper topics like diagonalization, stability, and dynamics.

62. Characteristic Polynomial (Where Eigenvalues Come From)

Eigenvalues don’t appear out of thin air - they come from the characteristic polynomial of a matrix. For a square matrix \(A\),

\[ p(\lambda) = \det(A - \lambda I) \]

The roots of this polynomial are the eigenvalues of \(A\).

Set Up Your Lab

import numpy as np
from sympy import Matrix, symbols

Step-by-Step Code Walkthrough

1. 2×2 example

\[ A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \]

λ = symbols('λ')
A = Matrix([[2,1],[1,2]])
char_poly = A.charpoly(λ)
print("Characteristic polynomial:", char_poly.as_expr())
print("Eigenvalues (roots):", char_poly.all_roots())

Characteristic polynomial: λ**2 - 4*λ + 3
Eigenvalues (roots): [1, 3]

Polynomial: \(\lambda^2 - 4\lambda + 3\). Roots: \(\lambda = 3, 1\).

2. Verify with eigen computation

print("Eigenvalues directly:", A.eigenvals())

Eigenvalues directly: {3: 1, 1: 1}

Matches the roots of the polynomial.

3. 3×3 example

B = Matrix([
    [1,2,3],
    [0,1,4],
    [5,6,0]
])

char_poly_B = B.charpoly(λ)
print("Characteristic polynomial of B:", char_poly_B.as_expr())
print("Eigenvalues of B:", char_poly_B.all_roots())

Characteristic polynomial of B: λ**3 - 2*λ**2 - 38*λ - 1
Eigenvalues of B: [CRootOf(x**3 - 2*x**2 - 38*x - 1, 0), CRootOf(x**3 - 2*x**2 - 38*x - 1, 1), CRootOf(x**3 - 2*x**2 - 38*x - 1, 2)]

4. NumPy version

NumPy doesn’t give the polynomial directly, but eigenvalues can be checked:

B_np = np.array([[1,2,3],[0,1,4],[5,6,0]], dtype=float)
eigvals = np.linalg.eigvals(B_np)
print("NumPy eigenvalues:", eigvals)

NumPy eigenvalues: [-5.2296696  -0.02635282  7.25602242]

5. Relation to trace and determinant

For a 2×2 matrix

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \]

the characteristic polynomial is

\[ \lambda^2 - (a+d)\lambda + (ad - bc). \]

• Coefficient of \(\lambda\): \(-\text{trace}(A)\).
• Constant term: \(\det(A)\).

print("Trace:", A.trace())
print("Determinant:", A.det())

Trace: 4
Determinant: 3

Try It Yourself

1. Compute the characteristic polynomial of

   \[ \begin{bmatrix} 4 & 0 \\ 0 & 5 \end{bmatrix} \]

   and confirm eigenvalues are 4 and 5.

2. Check the relationship between polynomial coefficients, trace, and determinant for a 3×3 case.

3. Verify with NumPy that the roots of the polynomial equal the eigenvalues.

The Takeaway

• The characteristic polynomial encodes eigenvalues as its roots.
• Coefficients are tied to invariants: trace and determinant.
• This polynomial viewpoint is the bridge from algebraic formulas to geometric eigen-behavior.

63. Algebraic vs. Geometric Multiplicity (How Many and How Independent)

Eigenvalues can repeat, and when they do, two notions of multiplicity arise:

• Algebraic multiplicity: how many times the eigenvalue appears as a root of the characteristic polynomial.
• Geometric multiplicity: the dimension of the eigenspace (number of independent eigenvectors).

Always:

\[ 1 \leq \text{geometric multiplicity} \leq \text{algebraic multiplicity} \]

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Matrix with repeated eigenvalue

A = Matrix([
    [2,1],
    [0,2]
])

print("Eigenvalues and algebraic multiplicity:", A.eigenvals())
print("Eigenvectors:", A.eigenvects())

Eigenvalues and algebraic multiplicity: {2: 2}
Eigenvectors: [(2, 2, [Matrix([
[1],
[0]])])]

• Eigenvalue 2 has algebraic multiplicity = 2.
• But only 1 independent eigenvector → geometric multiplicity = 1.

2. Diagonal matrix with repetition

B = Matrix([
    [3,0,0],
    [0,3,0],
    [0,0,3]
])

print("Eigenvalues:", B.eigenvals())
print("Eigenvectors:", B.eigenvects())

Eigenvalues: {3: 3}
Eigenvectors: [(3, 3, [Matrix([
[1],
[0],
[0]]), Matrix([
[0],
[1],
[0]]), Matrix([
[0],
[0],
[1]])])]

Here, eigenvalue 3 has algebraic multiplicity = 3, and geometric multiplicity = 3.

3. NumPy check

A_np = np.array([[2,1],[0,2]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A_np)
print("Eigenvalues:", eigvals)
print("Eigenvectors:\n", eigvecs)

Eigenvalues: [2. 2.]
Eigenvectors:
 [[ 1.0000000e+00 -1.0000000e+00]
 [ 0.0000000e+00  4.4408921e-16]]

NumPy won’t show multiplicities directly, but you can see repeated eigenvalues.

4. Comparing two cases

• Defective matrix: Algebraic > geometric (like the upper triangular \(A\)).
• Diagonalizable matrix: Algebraic = geometric (like \(B\)).

This distinction determines whether a matrix can be diagonalized.

Try It Yourself

1. Compute algebraic and geometric multiplicities of

   \[ \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \]

   (hint: only one eigenvector).

2. Take a diagonal matrix with repeated entries - what happens to multiplicities?

3. Test a random 3×3 singular matrix. Does 0 have algebraic multiplicity > 1?

The Takeaway

• Algebraic multiplicity = count of root in characteristic polynomial.
• Geometric multiplicity = dimension of eigenspace.
• If they match for all eigenvalues → matrix is diagonalizable.

64. Diagonalization (When a Matrix Becomes Simple)

A matrix \(A\) is diagonalizable if it can be written as

\[ A = P D P^{-1} \]

• \(D\) is diagonal (containing eigenvalues).
• Columns of \(P\) are the eigenvectors.

This means \(A\) acts like simple scaling in a “better” coordinate system.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. A diagonalizable 2×2 matrix

A = Matrix([
    [4,1],
    [2,3]
])

P, D = A.diagonalize()
print("P (eigenvectors):")
print(P)
print("D (eigenvalues on diagonal):")
print(D)

# Verify A = P D P^-1
print("Check:", P*D*P.inv())

P (eigenvectors):
Matrix([[-1, 1], [2, 1]])
D (eigenvalues on diagonal):
Matrix([[2, 0], [0, 5]])
Check: Matrix([[4, 1], [2, 3]])

2. A non-diagonalizable matrix

B = Matrix([
    [2,1],
    [0,2]
])

try:
    P, D = B.diagonalize()
    print("Diagonalization successful")
except Exception as e:
    print("Not diagonalizable:", e)

Not diagonalizable: Matrix is not diagonalizable

This fails because eigenvalue 2 has algebraic multiplicity 2 but geometric multiplicity 1.

3. Diagonalization with NumPy

NumPy doesn’t diagonalize explicitly, but we can build \(P\) and \(D\) ourselves:

A_np = np.array([[4,1],[2,3]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A_np)

P = eigvecs
D = np.diag(eigvals)
Pinv = np.linalg.inv(P)

print("Check A = PDP^-1:\n", P @ D @ Pinv)

Check A = PDP^-1:
 [[4. 1.]
 [2. 3.]]

4. Powers of a diagonalizable matrix

One reason diagonalization is powerful:

\[ A^k = P D^k P^{-1} \]

Since \(D^k\) is trivial (just raise each diagonal entry to power \(k\)).

k = 5

A_power = np.linalg.matrix_power(A, k)
D_power = np.linalg.matrix_power(D, k)
A_via_diag = P @ D_power @ np.linalg.inv(P)

print("A^5 via diagonalization:\n", A_via_diag)
print("Direct A^5:\n", A_power)

A^5 via diagonalization:
 [[2094. 1031.]
 [2062. 1063.]]
Direct A^5:
 [[2094 1031]
 [2062 1063]]

Both match.

Try It Yourself

1. Check whether

   \[ \begin{bmatrix} 5 & 0 \\ 0 & 5 \end{bmatrix} \]

   is diagonalizable.

2. Try diagonalizing a rotation matrix by 90°. Do you get complex eigenvalues?

3. Verify the formula \(A^k = P D^k P^{-1}\) for a 3×3 diagonalizable matrix.

The Takeaway

• Diagonalization rewrites a matrix in its simplest form.
• Works if there are enough independent eigenvectors.
• It makes powers of \(A\) easy, and is the gateway to analyzing dynamics.

65. Powers of a Matrix (Long-Term Behavior via Eigenvalues)

One of the most useful applications of eigenvalues and diagonalization is computing powers of a matrix:

\[ A^k = P D^k P^{-1} \]

where \(D\) is diagonal with eigenvalues of \(A\). Each eigenvalue \(\lambda\) raised to \(k\) dictates how its eigenvector direction grows, decays, or oscillates over time.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Simple diagonal matrix

If \(D = \text{diag}(2,3)\):

D = Matrix([[2,0],[0,3]])
print("D^5 =")
print(D**5)

D^5 =
Matrix([[32, 0], [0, 243]])

Eigenvalues are 2 and 3. Raising to the 5th power just raises each eigenvalue to the 5th: \(2^5, 3^5\).

2. Non-diagonal matrix

A = Matrix([
    [4,1],
    [2,3]
])

P, D = A.diagonalize()
print("D (eigenvalues):")
print(D)

# Compute A^10 via diagonalization
A10 = P * (D**10) * P.inv()
print("A^10 =")
print(A10)

D (eigenvalues):
Matrix([[2, 0], [0, 5]])
A^10 =
Matrix([[6510758, 3254867], [6509734, 3255891]])

Much easier than multiplying \(A\) ten times!

3. NumPy version

A_np = np.array([[4,1],[2,3]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A_np)

k = 10
D_power = np.diag(eigvals**k)
A10_np = eigvecs @ D_power @ np.linalg.inv(eigvecs)

print("A^10 via eigen-decomposition:\n", A10_np)

A^10 via eigen-decomposition:
 [[6510758. 3254867.]
 [6509734. 3255891.]]

4. Long-term behavior

Eigenvalues tell us what happens as \(k \to \infty\):

• If \(|\lambda| < 1\) → decay to 0.
• If \(|\lambda| > 1\) → grows unbounded.
• If \(|\lambda| = 1\) → oscillates or stabilizes.

B = Matrix([
    [0.5,0],
    [0,1.2]
])

P, D = B.diagonalize()
print("Eigenvalues:", D)
print("B^20:", P*(D**20)*P.inv())

Eigenvalues: Matrix([[0.500000000000000, 0], [0, 1.20000000000000]])
B^20: Matrix([[9.53674316406250e-7, 0], [0, 38.3375999244747]])

Here, the component along eigenvalue 0.5 decays, while eigenvalue 1.2 grows.

Try It Yourself

1. Compute \(A^{50}\) for a diagonal matrix with eigenvalues 0.9 and 1.1. Which component dominates?
2. Take a stochastic (Markov) matrix and compute powers. Do the rows stabilize?
3. Experiment with complex eigenvalues (like a rotation) and check if the powers oscillate.

The Takeaway

• Matrix powers are simple when using eigenvalues.
• Long-term dynamics are controlled by eigenvalue magnitudes.
• This insight is critical in Markov chains, stability analysis, and dynamical systems.

66. Real vs. Complex Spectra (Rotations and Oscillations)

Not all eigenvalues are real. Some matrices, especially those involving rotations, have complex eigenvalues. Complex eigenvalues often describe oscillations or rotations in systems.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Rotation matrix in 2D

A 90° rotation matrix:

\[ R = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \]

R = Matrix([[0, -1],
            [1,  0]])

print("Characteristic polynomial:", R.charpoly())
print("Eigenvalues:", R.eigenvals())

Characteristic polynomial: PurePoly(lambda**2 + 1, lambda, domain='ZZ')
Eigenvalues: {-I: 1, I: 1}

Result: eigenvalues are \(i\) and \(-i\) (purely imaginary).

2. Verify eigen-equation with complex numbers

eigs = R.eigenvects()
for eig in eigs:
    lam = eig[0]
    v = eig[2][0]
    print(f"λ = {lam}, Av = {R*v}, λv = {lam*v}")

λ = -I, Av = Matrix([[-1], [-I]]), λv = Matrix([[-1], [-I]])
λ = I, Av = Matrix([[-1], [I]]), λv = Matrix([[-1], [I]])

3. NumPy version

R_np = np.array([[0,-1],[1,0]], dtype=float)
eigvals, eigvecs = np.linalg.eig(R_np)
print("Eigenvalues:", eigvals)
print("Eigenvectors:\n", eigvecs)

Eigenvalues: [0.+1.j 0.-1.j]
Eigenvectors:
 [[0.70710678+0.j         0.70710678-0.j        ]
 [0.        -0.70710678j 0.        +0.70710678j]]

NumPy shows complex eigenvalues with j (Python’s imaginary unit).

4. Rotation by arbitrary angle

General 2D rotation:

\[ R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \]

Eigenvalues:

\[ \lambda = e^{\pm i\theta} = \cos\theta \pm i\sin\theta \]

theta = np.pi/4  # 45 degrees
R_theta = np.array([[np.cos(theta), -np.sin(theta)],
                    [np.sin(theta),  np.cos(theta)]])

eigvals, eigvecs = np.linalg.eig(R_theta)
print("Eigenvalues (rotation 45°):", eigvals)

Eigenvalues (rotation 45°): [0.70710678+0.70710678j 0.70710678-0.70710678j]

5. Oscillation insight

• Complex eigenvalues with \(|\lambda|=1\) → pure oscillation (no growth).
• If \(|\lambda|<1\) → decaying spiral.
• If \(|\lambda|>1\) → growing spiral.

Example:

A = np.array([[0.8, -0.6],
              [0.6,  0.8]])

eigvals, _ = np.linalg.eig(A)
print("Eigenvalues:", eigvals)

Eigenvalues: [0.8+0.6j 0.8-0.6j]

These eigenvalues lie inside the unit circle → spiral decay.

Try It Yourself

1. Compute eigenvalues of a 180° rotation. What happens?
2. Modify the rotation matrix to include scaling (e.g., multiply by 1.1). Do the eigenvalues lie outside the unit circle?
3. Plot the trajectory of repeatedly applying a rotation matrix to a vector.

The Takeaway

• Complex eigenvalues naturally appear in rotations and oscillatory systems.
• Their magnitude controls growth or decay; their angle controls oscillation.
• This is a key link between linear algebra and dynamics in physics and engineering.

67. Defective Matrices and a Peek at Jordan Form (When Diagonalization Fails)

Not every matrix has enough independent eigenvectors to be diagonalized. Such matrices are called defective. To handle them, mathematicians use the Jordan normal form, which extends diagonalization with extra structure.

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. A defective example

\[ A = \begin{bmatrix} 2 & 1 \\ 0 & 2 \end{bmatrix} \]

A = Matrix([[2,1],
            [0,2]])

print("Eigenvalues:", A.eigenvals())
print("Eigenvectors:", A.eigenvects())

Eigenvalues: {2: 2}
Eigenvectors: [(2, 2, [Matrix([
[1],
[0]])])]

• Eigenvalue 2 has algebraic multiplicity = 2.
• Only 1 eigenvector exists → geometric multiplicity = 1.

Thus \(A\) is defective, not diagonalizable.

2. Attempt diagonalization

try:
    P, D = A.diagonalize()
    print("Diagonal form:", D)
except Exception as e:
    print("Diagonalization failed:", e)

Diagonalization failed: Matrix is not diagonalizable

You’ll see an error - confirming \(A\) is not diagonalizable.

3. Jordan form in SymPy

J, P = A.jordan_form()
print("Jordan form J:")
print(J)
print("P (generalized eigenvectors):")
print(P)

Jordan form J:
Matrix([[1, 0], [0, 1]])
P (generalized eigenvectors):
Matrix([[2, 1], [0, 2]])

The Jordan form shows a Jordan block:

\[ J = \begin{bmatrix} 2 & 1 \\ 0 & 2 \end{bmatrix} \]

This block structure represents the failure of diagonalization.

4. NumPy perspective

NumPy doesn’t compute Jordan form, but you can see repeated eigenvalues and lack of eigenvectors:

A_np = np.array([[2,1],[0,2]], dtype=float)
eigvals, eigvecs = np.linalg.eig(A_np)
print("Eigenvalues:", eigvals)
print("Eigenvectors:\n", eigvecs)

Eigenvalues: [2. 2.]
Eigenvectors:
 [[ 1.0000000e+00 -1.0000000e+00]
 [ 0.0000000e+00  4.4408921e-16]]

The eigenvectors matrix has fewer independent columns than expected.

5. Generalized eigenvectors

Jordan form introduces generalized eigenvectors, which satisfy:

\[ (A - \lambda I)^k v = 0 \quad \text{for some } k>1 \]

They “fill the gap” when ordinary eigenvectors are insufficient.

Try It Yourself

1. Test diagonalizability of

   \[ \begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix} \]

   and compare with its Jordan form.

2. Try a 3×3 defective matrix with one Jordan block of size 3.

3. Verify that Jordan blocks still capture the correct eigenvalues.

The Takeaway

• Defective matrices lack enough eigenvectors for diagonalization.
• Jordan form replaces diagonalization with blocks, keeping eigenvalues on the diagonal.
• Understanding Jordan blocks is essential for advanced linear algebra and differential equations.

68. Stability and Spectral Radius (Grow, Decay, or Oscillate)

The spectral radius of a matrix \(A\) is defined as

\[ \rho(A) = \max_i |\lambda_i| \]

where \(\lambda_i\) are the eigenvalues. It tells us the long-term behavior of repeated applications of \(A\):

• If \(\rho(A) < 1\) → powers of \(A\) tend to 0 (stable/decay).
• If \(\rho(A) = 1\) → powers neither blow up nor vanish (neutral, may oscillate).
• If \(\rho(A) > 1\) → powers diverge (unstable/growth).

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Stable matrix (\(\rho < 1\))

A = np.array([[0.5, 0],
              [0, 0.3]])

eigvals = np.linalg.eigvals(A)
spectral_radius = max(abs(eigvals))

print("Eigenvalues:", eigvals)
print("Spectral radius:", spectral_radius)

print("A^10:\n", np.linalg.matrix_power(A, 10))

Eigenvalues: [0.5 0.3]
Spectral radius: 0.5
A^10:
 [[9.765625e-04 0.000000e+00]
 [0.000000e+00 5.904900e-06]]

All entries shrink toward zero.

2. Unstable matrix (\(\rho > 1\))

B = np.array([[1.2, 0],
              [0, 0.9]])

eigvals = np.linalg.eigvals(B)
print("Eigenvalues:", eigvals, "Spectral radius:", max(abs(eigvals)))
print("B^10:\n", np.linalg.matrix_power(B, 10))

Eigenvalues: [1.2 0.9] Spectral radius: 1.2
B^10:
 [[6.19173642 0.        ]
 [0.         0.34867844]]

The component along eigenvalue 1.2 grows quickly.

3. Neutral/oscillatory case (\(\rho = 1\))

90° rotation matrix:

R = np.array([[0, -1],
              [1,  0]])

eigvals = np.linalg.eigvals(R)
print("Eigenvalues:", eigvals)
print("Spectral radius:", max(abs(eigvals)))
print("R^4:\n", np.linalg.matrix_power(R, 4))

Eigenvalues: [0.+1.j 0.-1.j]
Spectral radius: 1.0
R^4:
 [[1 0]
 [0 1]]

Eigenvalues are ±i, with modulus 1 → pure oscillation.

4. Spectral radius with SymPy

M = Matrix([[2,1],[1,2]])
eigs = M.eigenvals()
print("Eigenvalues:", eigs)
print("Spectral radius:", max(abs(ev) for ev in eigs))

Eigenvalues: {3: 1, 1: 1}
Spectral radius: 3

Try It Yourself

1. Build a diagonal matrix with entries 0.8, 1.0, and 1.1. Predict which direction dominates as powers grow.
2. Apply a random matrix repeatedly to a vector. Does it shrink, grow, or oscillate?
3. Check if a Markov chain transition matrix always has spectral radius 1.

The Takeaway

• The spectral radius is the key number that predicts growth, decay, or oscillation.
• Long-term stability in dynamical systems is governed entirely by eigenvalue magnitudes.
• This connects linear algebra directly to control theory, Markov chains, and differential equations.

69. Markov Chains and Steady States (Probabilities as Linear Algebra)

A Markov chain is a process that moves between states according to probabilities. The transitions are encoded in a stochastic matrix \(P\):

• Each entry \(p_{ij} \geq 0\)
• Each row sums to 1

If we start with a probability vector \(v_0\), then after \(k\) steps:

\[ v_k = v_0 P^k \]

A steady state is a probability vector \(v\) such that \(vP = v\). It corresponds to eigenvalue \(\lambda = 1\).

Set Up Your Lab

import numpy as np
from sympy import Matrix

Step-by-Step Code Walkthrough

1. Simple two-state chain

P = np.array([
    [0.9, 0.1],
    [0.5, 0.5]
])

v0 = np.array([1.0, 0.0])  # start in state 1
for k in [1, 2, 5, 10, 50]:
    vk = v0 @ np.linalg.matrix_power(P, k)
    print(f"Step {k}: {vk}")

Step 1: [0.9 0.1]
Step 2: [0.86 0.14]
Step 5: [0.83504 0.16496]
Step 10: [0.83335081 0.16664919]
Step 50: [0.83333333 0.16666667]

The distribution stabilizes as \(k\) increases.

2. Steady state via eigenvector

Find eigenvector for eigenvalue 1:

eigvals, eigvecs = np.linalg.eig(P.T)
steady_state = eigvecs[:, np.isclose(eigvals, 1)]
steady_state = steady_state / steady_state.sum()
print("Steady state:", steady_state.real.flatten())

Steady state: [0.83333333 0.16666667]

3. SymPy exact check

P_sym = Matrix([[0.9,0.1],[0.5,0.5]])
steady = P_sym.eigenvects()
print("Eigen info:", steady)

Eigen info: [(1.00000000000000, 1, [Matrix([
[0.707106781186548],
[0.707106781186547]])]), (0.400000000000000, 1, [Matrix([
[-0.235702260395516],
[  1.17851130197758]])])]

4. A 3-state example

Q = np.array([
    [0.3, 0.7, 0.0],
    [0.2, 0.5, 0.3],
    [0.1, 0.2, 0.7]
])

eigvals, eigvecs = np.linalg.eig(Q.T)
steady = eigvecs[:, np.isclose(eigvals, 1)]
steady = steady / steady.sum()
print("Steady state for Q:", steady.real.flatten())

Steady state for Q: [0.17647059 0.41176471 0.41176471]

Try It Yourself

1. Create a transition matrix where one state is absorbing (e.g., row = [0,0,1]). What happens to the steady state?
2. Simulate a random walk on 3 states. Does the steady state distribute evenly?
3. Compare long-run simulation with eigenvector computation.

The Takeaway

• Markov chains evolve by repeated multiplication with a stochastic matrix.
• Steady states are eigenvectors with eigenvalue 1.
• This framework powers real applications like PageRank, weather models, and queuing systems.

70. Linear Differential Systems (Solutions via Eigen-Decomposition)

Linear differential equations often reduce to systems of the form:

\[ \frac{d}{dt}x(t) = A x(t) \]

where \(A\) is a matrix and \(x(t)\) is a vector of functions. The solution is given by the matrix exponential:

\[ x(t) = e^{At} x(0) \]

If \(A\) is diagonalizable, this becomes simple using eigenvalues and eigenvectors.

Set Up Your Lab

import numpy as np
from sympy import Matrix, exp, symbols
from scipy.linalg import expm

Step-by-Step Code Walkthrough

1. Simple system with diagonal matrix

\[ A = \begin{bmatrix} -1 & 0 \\ 0 & 2 \end{bmatrix} \]

A = Matrix([[-1,0],
            [0, 2]])
t = symbols('t')
expAt = (A*t).exp()
print("e^{At} =")
print(expAt)

e^{At} =
Matrix([[exp(-t), 0], [0, exp(2*t)]])

Solution:

\[ x(t) = \begin{bmatrix} e^{-t} & 0 \\ 0 & e^{2t} \end{bmatrix} x(0) \]

One component decays, the other grows.

2. Non-diagonal example

B = Matrix([[0,1],
            [-2,-3]])
expBt = (B*t).exp()
print("e^{Bt} =")
print(expBt)

e^{Bt} =
Matrix([[2*exp(-t) - exp(-2*t), exp(-t) - exp(-2*t)], [-2*exp(-t) + 2*exp(-2*t), -exp(-t) + 2*exp(-2*t)]])

Here the solution involves exponentials and possibly sines/cosines (oscillatory behavior).

3. Numeric computation with SciPy

import numpy as np
from scipy.linalg import expm

A = np.array([[-1,0],[0,2]], dtype=float)
t = 1.0
print("Matrix exponential e^{At} at t=1:\n", expm(A*t))

Matrix exponential e^{At} at t=1:
 [[0.36787944 0.        ]
 [0.         7.3890561 ]]

This computes \(e^{At}\) numerically.

4. Simulation of a trajectory

x0 = np.array([1.0, 1.0])
for t in [0, 0.5, 1, 2]:
    xt = expm(A*t) @ x0
    print(f"x({t}) = {xt}")

x(0) = [1. 1.]
x(0.5) = [0.60653066 2.71828183]
x(1) = [0.36787944 7.3890561 ]
x(2) = [ 0.13533528 54.59815003]

One coordinate decays, the other explodes with time.

Try It Yourself

1. Solve the system \(\dot{x} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}x\). What kind of motion do you see?
2. Use SciPy to simulate a system with eigenvalues less than 0. Does it always decay?
3. Try an unstable system with eigenvalues > 0 and watch how trajectories diverge.

The Takeaway

• Linear systems \(\dot{x} = Ax\) are solved via the matrix exponential.
• Eigenvalues determine stability: negative real parts = stable, positive = unstable, imaginary = oscillations.
• This ties linear algebra directly to differential equations and dynamical systems.

Chapter 8. Orthogonality, least squars, and QR

71. Inner Products Beyond Dot Product (Custom Notions of Angle)

The dot product is the standard inner product in \(\mathbb{R}^n\), but linear algebra allows us to define more general inner products that measure length and angle in different ways.

An inner product on a vector space is a function \(\langle u, v \rangle\) that satisfies:

1. Linearity in the first argument.
2. Symmetry: \(\langle u, v \rangle = \langle v, u \rangle\).
3. Positive definiteness: \(\langle v, v \rangle \geq 0\) and equals 0 only if \(v=0\).

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Standard dot product

u = np.array([1,2,3])
v = np.array([4,5,6])

print("Dot product:", np.dot(u,v))

Dot product: 32

This is the familiar formula: \(1·4 + 2·5 + 3·6 = 32\).

2. Weighted inner product

We can define:

\[ \langle u, v \rangle_W = u^T W v \]

where \(W\) is a positive definite matrix.

W = np.array([[2,0,0],
              [0,1,0],
              [0,0,3]])

def weighted_inner(u,v,W):
    return u.T @ W @ v

print("Weighted inner product:", weighted_inner(u,v,W))

Weighted inner product: 72

Here, some coordinates “count more” than others.

3. Check symmetry and positivity

print("⟨u,v⟩ == ⟨v,u⟩ ?", weighted_inner(u,v,W) == weighted_inner(v,u,W))
print("⟨u,u⟩ (should be >0):", weighted_inner(u,u,W))

⟨u,v⟩ == ⟨v,u⟩ ? True
⟨u,u⟩ (should be >0): 33

4. Angle with weighted inner product

\[ \cos\theta = \frac{\langle u,v \rangle_W}{\|u\|_W \, \|v\|_W} \]

def weighted_norm(u,W):
    return np.sqrt(weighted_inner(u,u,W))

cos_theta = weighted_inner(u,v,W) / (weighted_norm(u,W) * weighted_norm(v,W))
print("Cosine of angle (weighted):", cos_theta)

Cosine of angle (weighted): 0.97573875381809

5. Custom example: correlation inner product

For statistics, an inner product can be defined as covariance or correlation. Example with mean-centered vectors:

x = np.array([2,4,6])
y = np.array([1,3,5])

x_centered = x - x.mean()
y_centered = y - y.mean()

corr_inner = np.dot(x_centered,y_centered)
print("Correlation-style inner product:", corr_inner)

Correlation-style inner product: 8.0

Try It Yourself

1. Define a custom inner product with \(W = \text{diag}(1,10,100)\). How does it change angles between vectors?
2. Verify positivity: compute \(\langle v, v \rangle_W\) for a random vector \(v\).
3. Compare dot product vs weighted inner product on the same pair of vectors.

The Takeaway

• Inner products generalize the dot product to new “geometries.”
• By changing the weight matrix \(W\), you change how lengths and angles are measured.
• This flexibility is essential in statistics, optimization, and machine learning.

72. Orthogonality and Orthonormal Bases (Perpendicular Power)

Two vectors are orthogonal if their inner product is zero:

\[ \langle u, v \rangle = 0 \]

If, in addition, each vector has length 1, the set is orthonormal. Orthonormal bases are extremely useful because they simplify computations: projections, decompositions, and coordinate changes all become clean.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Check orthogonality

u = np.array([1, -1])
v = np.array([1, 1])

print("Dot product:", np.dot(u,v))

Dot product: 0

Since the dot product is 0, they’re orthogonal.

2. Normalizing vectors

\[ \hat{u} = \frac{u}{\|u\|} \]

def normalize(vec):
    return vec / np.linalg.norm(vec)

u_norm = normalize(u)
v_norm = normalize(v)

print("Normalized u:", u_norm)
print("Normalized v:", v_norm)

Normalized u: [ 0.70710678 -0.70710678]
Normalized v: [0.70710678 0.70710678]

Now both have length 1.

3. Form an orthonormal basis

basis = np.column_stack((u_norm, v_norm))
print("Orthonormal basis:\n", basis)

print("Check inner products:\n", basis.T @ basis)

Orthonormal basis:
 [[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]
Check inner products:
 [[ 1.00000000e+00 -2.23711432e-17]
 [-2.23711432e-17  1.00000000e+00]]

The result is the identity matrix → perfectly orthonormal.

4. Apply to coordinates

If \(x = [2,3]\), coordinates in the orthonormal basis are:

x = np.array([2,3])
coords = basis.T @ x
print("Coordinates in new basis:", coords)
print("Reconstruction:", basis @ coords)

Coordinates in new basis: [-0.70710678  3.53553391]
Reconstruction: [2. 3.]

It reconstructs exactly.

5. Random example with QR

Any set of linearly independent vectors can be orthonormalized (Gram–Schmidt, or QR decomposition):

M = np.random.rand(3,3)
Q, R = np.linalg.qr(M)
print("Q (orthonormal basis):\n", Q)
print("Check Q^T Q = I:\n", Q.T @ Q)

Q (orthonormal basis):
 [[-0.37617518  0.91975919 -0.111961  ]
 [-0.82070726 -0.38684608 -0.42046368]
 [-0.430037   -0.06628079  0.90037494]]
Check Q^T Q = I:
 [[1.00000000e+00 5.55111512e-17 5.55111512e-17]
 [5.55111512e-17 1.00000000e+00 3.47849792e-17]
 [5.55111512e-17 3.47849792e-17 1.00000000e+00]]

Try It Yourself

1. Create two 3D vectors and check if they’re orthogonal.
2. Normalize them to form an orthonormal set.
3. Use np.linalg.qr on a 4×3 random matrix and verify that the columns of \(Q\) are orthonormal.

The Takeaway

• Orthogonality means perpendicularity; orthonormality adds unit length.
• Orthonormal bases simplify coordinate systems, making inner products and projections easy.
• QR decomposition is the practical tool to generate orthonormal bases in higher dimensions.

73. Gram–Schmidt Process (Constructing Orthonormal Bases)

The Gram–Schmidt process takes a set of linearly independent vectors and turns them into an orthonormal basis. This is crucial for working with subspaces, projections, and numerical stability.

Given vectors \(v_1, v_2, \dots, v_n\):

1. Set \(u_1 = v_1\).

2. Subtract projections to make each new vector orthogonal to the earlier ones:

   \[ u_k = v_k - \sum_{j=1}^{k-1} \frac{\langle v_k, u_j \rangle}{\langle u_j, u_j \rangle} u_j \]

3. Normalize:

   \[ e_k = \frac{u_k}{\|u_k\|} \]

The set \(\{e_1, e_2, \dots, e_n\}\) is orthonormal.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Define vectors

v1 = np.array([1.0, 1.0, 0.0])
v2 = np.array([1.0, 0.0, 1.0])
v3 = np.array([0.0, 1.0, 1.0])
V = [v1, v2, v3]

2. Implement Gram–Schmidt

def gram_schmidt(V):
    U = []
    for v in V:
        u = v.copy()
        for uj in U:
            u -= np.dot(v, uj) / np.dot(uj, uj) * uj
        U.append(u)
    # Normalize
    E = [u/np.linalg.norm(u) for u in U]
    return np.array(E)

E = gram_schmidt(V)
print("Orthonormal basis:\n", E)
print("Check orthonormality:\n", np.round(E @ E.T, 6))

Orthonormal basis:
 [[ 0.70710678  0.70710678  0.        ]
 [ 0.40824829 -0.40824829  0.81649658]
 [-0.57735027  0.57735027  0.57735027]]
Check orthonormality:
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

3. Compare with NumPy QR

Q, R = np.linalg.qr(np.column_stack(V))
print("QR-based orthonormal basis:\n", Q)
print("Check Q^T Q = I:\n", np.round(Q.T @ Q, 6))

QR-based orthonormal basis:
 [[-0.70710678  0.40824829 -0.57735027]
 [-0.70710678 -0.40824829  0.57735027]
 [-0.          0.81649658  0.57735027]]
Check Q^T Q = I:
 [[ 1.  0. -0.]
 [ 0.  1. -0.]
 [-0. -0.  1.]]

Both methods give orthonormal bases.

4. Application: projection

To project a vector \(x\) onto the span of \(V\):

x = np.array([2.0, 2.0, 2.0])
proj = sum((x @ e) * e for e in E)
print("Projection of x onto span(V):", proj)

Projection of x onto span(V): [2. 2. 2.]

Try It Yourself

1. Run Gram–Schmidt on two vectors in 2D. Compare with just normalizing and checking orthogonality.
2. Replace one vector with a linear combination of others. What happens?
3. Use QR decomposition on a 4×3 random matrix and compare with Gram–Schmidt.

The Takeaway

• Gram–Schmidt converts arbitrary independent vectors into an orthonormal basis.
• Orthonormal bases simplify projections, decompositions, and computations.
• In practice, QR decomposition is often used as a numerically stable implementation.

74. Orthogonal Projections onto Subspaces (Closest Point Principle)

Given a subspace spanned by vectors, the orthogonal projection of a vector \(x\) onto the subspace is the point in the subspace that is closest to \(x\). This is a cornerstone idea in least squares, data fitting, and signal processing.

Formula Recap

If \(Q\) is a matrix with orthonormal columns spanning the subspace, the projection of \(x\) is:

\[ \text{proj}(x) = Q Q^T x \]

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Projection onto a line (1D subspace)

Suppose the subspace is spanned by \(u = [1,2]\).

u = np.array([1.0,2.0])
x = np.array([3.0,1.0])

u_norm = u / np.linalg.norm(u)
proj = np.dot(x, u_norm) * u_norm
print("Projection of x onto span(u):", proj)

Projection of x onto span(u): [1. 2.]

This gives the closest point to \(x\) along the line spanned by \(u\).

2. Projection onto a plane (2D subspace in 3D)

u1 = np.array([1.0,0.0,0.0])
u2 = np.array([0.0,1.0,0.0])
Q = np.column_stack([u1,u2])   # Orthonormal basis for xy-plane

x = np.array([2.0,3.0,5.0])
proj = Q @ Q.T @ x
print("Projection of x onto xy-plane:", proj)

Projection of x onto xy-plane: [2. 3. 0.]

Result drops the z-component → projection onto the plane.

3. General projection using QR

A = np.array([[1,1,0],
              [0,1,1],
              [1,0,1]], dtype=float)

Q, R = np.linalg.qr(A)
Q = Q[:, :2]   # take first 2 independent columns
x = np.array([2,2,2], dtype=float)

proj = Q @ Q.T @ x
print("Projection of x onto span(A):", proj)

Projection of x onto span(A): [2.66666667 1.33333333 1.33333333]

4. Visualization (2D case)

import matplotlib.pyplot as plt

plt.quiver(0,0,x[0],x[1],angles='xy',scale_units='xy',scale=1,color='red',label="x")
plt.quiver(0,0,proj[0],proj[1],angles='xy',scale_units='xy',scale=1,color='blue',label="Projection")
plt.quiver(0,0,u[0],u[1],angles='xy',scale_units='xy',scale=1,color='green',label="Subspace")
plt.axis('equal'); plt.grid(); plt.legend(); plt.show()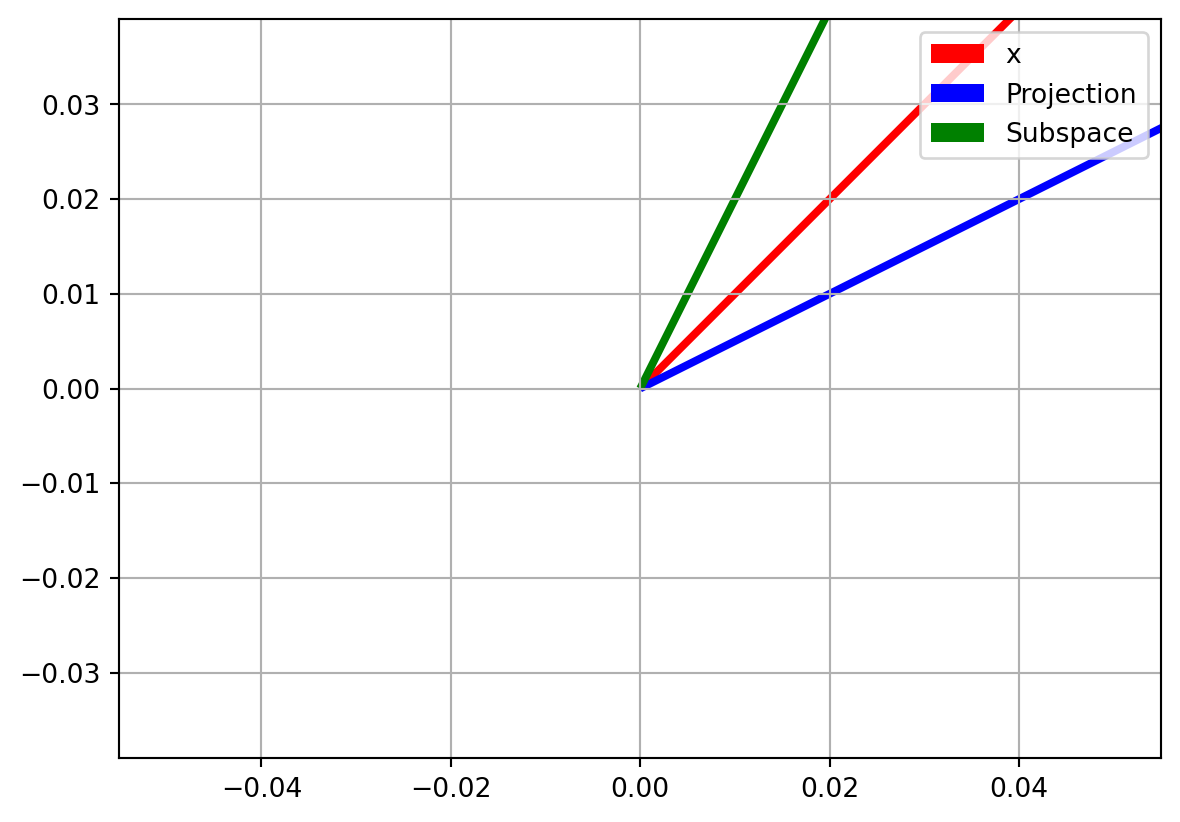

Try It Yourself

1. Project a vector onto the line spanned by \([2,1]\).
2. Project \([1,2,3]\) onto the plane spanned by \([1,0,1]\) and \([0,1,1]\).
3. Compare projection via formula \(Q Q^T x\) with manually solving least squares.

The Takeaway

• Orthogonal projection finds the closest point in a subspace.
• Formula \(Q Q^T x\) works perfectly when \(Q\) has orthonormal columns.
• Projections are the foundation of least squares, PCA, and many geometric algorithms.

75. Least-Squares Problems (Fit When Exact Solve Is Impossible)

Sometimes a system of equations \(Ax = b\) has no exact solution - usually because it’s overdetermined (more equations than unknowns). In this case, we look for an approximate solution \(x^*\) that minimizes the error:

\[ x^* = \arg\min_x \|Ax - b\|^2 \]

This is the least-squares solution, which geometrically is the projection of \(b\) onto the column space of \(A\).

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Overdetermined system

3 equations, 2 unknowns:

A = np.array([[1,1],
              [1,2],
              [1,3]], dtype=float)
b = np.array([6, 0, 0], dtype=float)

2. Solve least squares with NumPy

x_star, residuals, rank, s = np.linalg.lstsq(A, b, rcond=None)
print("Least squares solution:", x_star)
print("Residual norm squared:", residuals)

Least squares solution: [ 8. -3.]
Residual norm squared: [6.]

3. Compare with normal equations

\[ A^T A x = A^T b \]

x_normal = np.linalg.inv(A.T @ A) @ (A.T @ b)
print("Solution via normal equations:", x_normal)

Solution via normal equations: [ 8. -3.]

4. Geometric picture

The least-squares solution projects \(b\) onto the column space of \(A\):

proj = A @ x_star
print("Projection of b onto Col(A):", proj)
print("Original b:", b)
print("Error vector (b - proj):", b - proj)

Projection of b onto Col(A): [ 5.  2. -1.]
Original b: [6. 0. 0.]
Error vector (b - proj): [ 1. -2.  1.]

The error vector is orthogonal to the column space.

5. Verify orthogonality condition

\[ A^T (b - Ax^*) = 0 \]

print("Check orthogonality:", A.T @ (b - A @ x_star))

Check orthogonality: [0. 0.]

The result should be (close to) zero.

Try It Yourself

1. Create a taller \(A\) (say 5×2) with random numbers and solve least squares for a random \(b\).
2. Compare the residual from np.linalg.lstsq with geometric intuition (projection).
3. Modify \(b\) so that the system has an exact solution. Check if least squares gives it exactly.

The Takeaway

• Least-squares finds the best-fit solution when no exact solution exists.
• It works by projecting \(b\) onto the column space of \(A\).
• This principle underlies regression, curve fitting, and countless applications in data science.

76. Normal Equations and Geometry of Residuals (Why It Works)

The least-squares solution can be found by solving the normal equations:

\[ A^T A x = A^T b \]

This comes from the condition that the residual vector

\[ r = b - Ax \]

is orthogonal to the column space of \(A\).

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Build an overdetermined system

A = np.array([[1,1],
              [1,2],
              [1,3]], dtype=float)
b = np.array([6, 0, 0], dtype=float)

2. Solve least squares via normal equations

ATA = A.T @ A
ATb = A.T @ b
x_star = np.linalg.solve(ATA, ATb)

print("Least-squares solution x*:", x_star)

Least-squares solution x*: [ 8. -3.]

3. Compute residual and check orthogonality

residual = b - A @ x_star
print("Residual vector:", residual)
print("Check A^T r ≈ 0:", A.T @ residual)

Residual vector: [ 1. -2.  1.]
Check A^T r ≈ 0: [0. 0.]

This verifies the residual is perpendicular to the column space of \(A\).

4. Compare with NumPy’s least squares solver

x_lstsq, *_ = np.linalg.lstsq(A, b, rcond=None)
print("NumPy lstsq solution:", x_lstsq)

NumPy lstsq solution: [ 8. -3.]

The solutions should match (within numerical precision).

5. Geometric picture

• \(b\) is a point in \(\mathbb{R}^3\).
• \(Ax\) is restricted to lie in the 2D column space of \(A\).
• The least-squares solution picks the \(Ax\) closest to \(b\).
• The error vector \(r = b - Ax^*\) is orthogonal to the subspace.

proj = A @ x_star
print("Projection of b onto Col(A):", proj)

Projection of b onto Col(A): [ 5.  2. -1.]

Try It Yourself

1. Change \(b\) to \([1,1,1]\). Solve again and check the residual.
2. Use a random tall \(A\) (say 6×2) and verify that the residual is always orthogonal.
3. Compute \(\|r\|\) and see how it changes when you change \(b\).

The Takeaway

• Least squares works by making the residual orthogonal to the column space.
• Normal equations are the algebraic way to encode this condition.
• This orthogonality principle is the geometric heart of least-squares fitting.

77. QR Factorization (Stable Least Squares via Orthogonality)

While normal equations solve least squares, they can be numerically unstable if \(A^T A\) is ill-conditioned. A more stable method uses QR factorization:

\[ A = Q R \]

• \(Q\): matrix with orthonormal columns
• \(R\): upper triangular matrix

Then the least-squares problem reduces to solving:

\[ Rx = Q^T b \]

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Overdetermined system

A = np.array([[1,1],
              [1,2],
              [1,3]], dtype=float)
b = np.array([6, 0, 0], dtype=float)

2. QR factorization

Q, R = np.linalg.qr(A)
print("Q (orthonormal basis):\n", Q)
print("R (upper triangular):\n", R)

Q (orthonormal basis):
 [[-5.77350269e-01  7.07106781e-01]
 [-5.77350269e-01 -1.73054947e-16]
 [-5.77350269e-01 -7.07106781e-01]]
R (upper triangular):
 [[-1.73205081 -3.46410162]
 [ 0.         -1.41421356]]

3. Solve least squares using QR

y = Q.T @ b
x_star = np.linalg.solve(R[:2,:], y[:2])  # only top rows matter
print("Least squares solution via QR:", x_star)

Least squares solution via QR: [ 8. -3.]

4. Compare with NumPy’s lstsq

x_lstsq, *_ = np.linalg.lstsq(A, b, rcond=None)
print("NumPy lstsq:", x_lstsq)

NumPy lstsq: [ 8. -3.]

The answers should match closely.

5. Residual check

residual = b - A @ x_star
print("Residual vector:", residual)
print("Check orthogonality (Q^T r):", Q.T @ residual)

Residual vector: [ 1. -2.  1.]
Check orthogonality (Q^T r): [0.00000000e+00 3.46109895e-16]

Residual is orthogonal to the column space, confirming correctness.

Try It Yourself

1. Solve least squares for a 5×2 random matrix using both normal equations and QR. Compare results.
2. Check stability by making columns of \(A\) nearly dependent - see if QR behaves better than normal equations.
3. Compute projection of \(b\) using \(Q Q^T b\) and confirm it equals \(A x^*\).

The Takeaway

• QR factorization provides a numerically stable way to solve least squares.
• It avoids the instability of normal equations.
• In practice, modern solvers (like NumPy’s lstsq) rely on QR or SVD under the hood.

78. Orthogonal Matrices (Length-Preserving Transforms)

An orthogonal matrix \(Q\) is a square matrix whose columns (and rows) are orthonormal vectors. Formally:

\[ Q^T Q = Q Q^T = I \]

Key properties:

• Preserves lengths: \(\|Qx\| = \|x\|\)
• Preserves dot products: \(\langle Qx, Qy \rangle = \langle x, y \rangle\)
• Determinant is either \(+1\) (rotation) or \(-1\) (reflection)

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Construct a simple orthogonal matrix

90° rotation in 2D:

Q = np.array([[0, -1],
              [1,  0]])

print("Q^T Q =\n", Q.T @ Q)

Q^T Q =
 [[1 0]
 [0 1]]

Result = identity → confirms orthogonality.

2. Check length preservation

x = np.array([3,4])
print("Original length:", np.linalg.norm(x))
print("Transformed length:", np.linalg.norm(Q @ x))

Original length: 5.0
Transformed length: 5.0

Both lengths match.

3. Check dot product preservation

u = np.array([1,0])
v = np.array([0,1])

print("Dot(u,v):", np.dot(u,v))
print("Dot(Q u, Q v):", np.dot(Q @ u, Q @ v))

Dot(u,v): 0
Dot(Q u, Q v): 0

Dot product is preserved.

4. Reflection matrix

Reflection about the x-axis:

R = np.array([[1,0],
              [0,-1]])

print("R^T R =\n", R.T @ R)
print("Determinant of R:", np.linalg.det(R))

R^T R =
 [[1 0]
 [0 1]]
Determinant of R: -1.0

Determinant = -1 → reflection.

5. Random orthogonal matrix via QR

M = np.random.rand(3,3)
Q, _ = np.linalg.qr(M)
print("Q (random orthogonal):\n", Q)
print("Check Q^T Q ≈ I:\n", np.round(Q.T @ Q, 6))

Q (random orthogonal):
 [[-0.59472353  0.03725157 -0.80306677]
 [-0.61109913 -0.67000966  0.42147943]
 [-0.52236172  0.74141714  0.42123492]]
Check Q^T Q ≈ I:
 [[ 1.  0. -0.]
 [ 0.  1. -0.]
 [-0. -0.  1.]]

Try It Yourself

1. Build a 2D rotation matrix for 45°. Verify it’s orthogonal.
2. Check whether scaling matrices (e.g., \(\text{diag}(2,1)\)) are orthogonal. Why or why not?
3. Generate a random orthogonal matrix with np.linalg.qr and test its determinant.

The Takeaway

• Orthogonal matrices are rigid motions: they rotate or reflect without distorting lengths or angles.
• They play a key role in numerical stability, geometry, and physics.
• Every orthonormal basis corresponds to an orthogonal matrix.

79. Fourier Viewpoint (Expanding in Orthogonal Waves)

The Fourier viewpoint treats functions or signals as combinations of orthogonal waves (sines and cosines). This is just linear algebra: sine and cosine functions form an orthogonal basis, and any signal can be expressed as a linear combination of them.

Formula Recap

For a discrete signal \(x\), the Discrete Fourier Transform (DFT) is:

\[ X_k = \sum_{n=0}^{N-1} x_n e^{-2\pi i kn / N}, \quad k=0,\dots,N-1 \]

The inverse DFT reconstructs the signal. Orthogonality of complex exponentials makes this work.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Build a simple signal

t = np.linspace(0, 1, 100, endpoint=False)
signal = np.sin(2*np.pi*3*t) + 0.5*np.sin(2*np.pi*5*t)
plt.plot(t, signal)
plt.title("Signal = sin(3Hz) + 0.5 sin(5Hz)")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.show()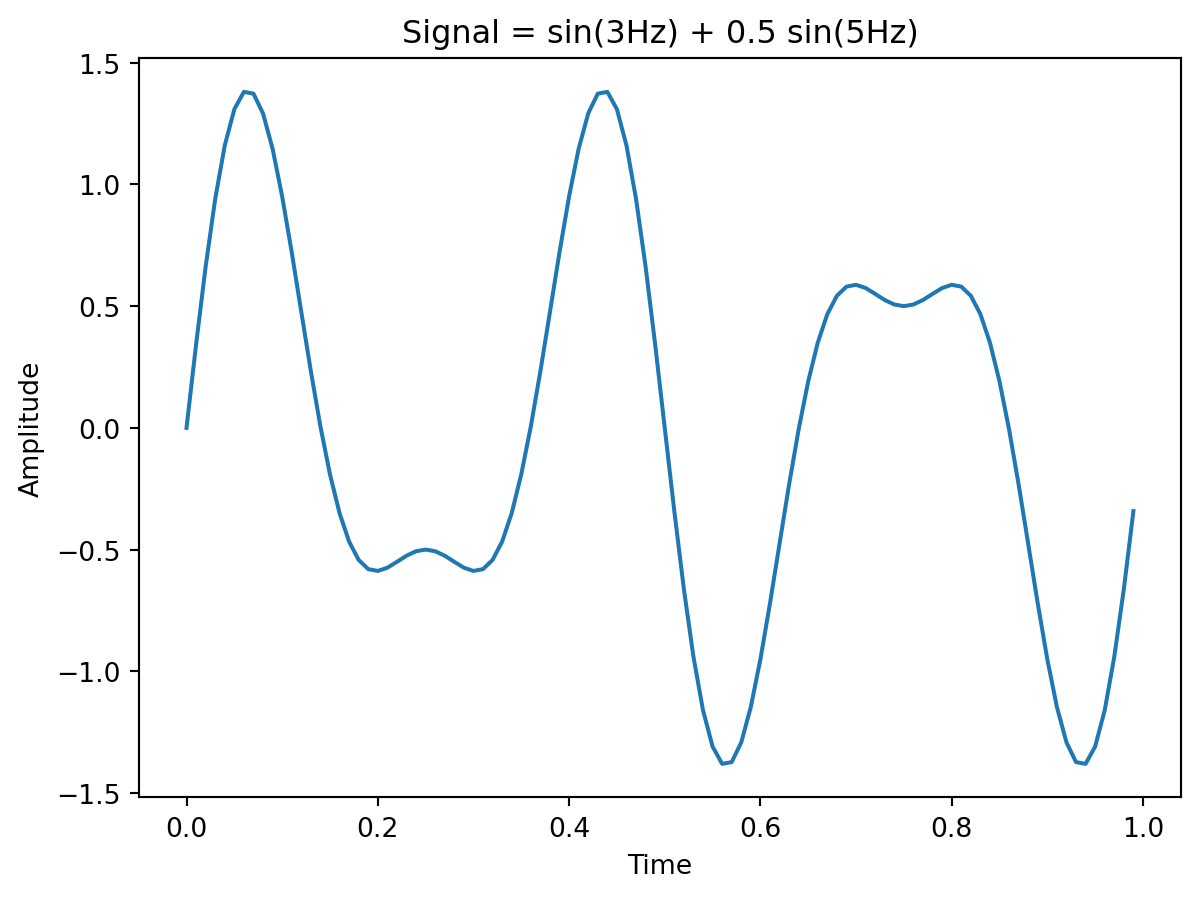

2. Compute Fourier transform (DFT)

X = np.fft.fft(signal)
freqs = np.fft.fftfreq(len(t), d=1/100)  # sampling rate = 100Hz

plt.stem(freqs[:50], np.abs(X[:50]), basefmt=" ")
plt.title("Fourier spectrum")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude")
plt.show()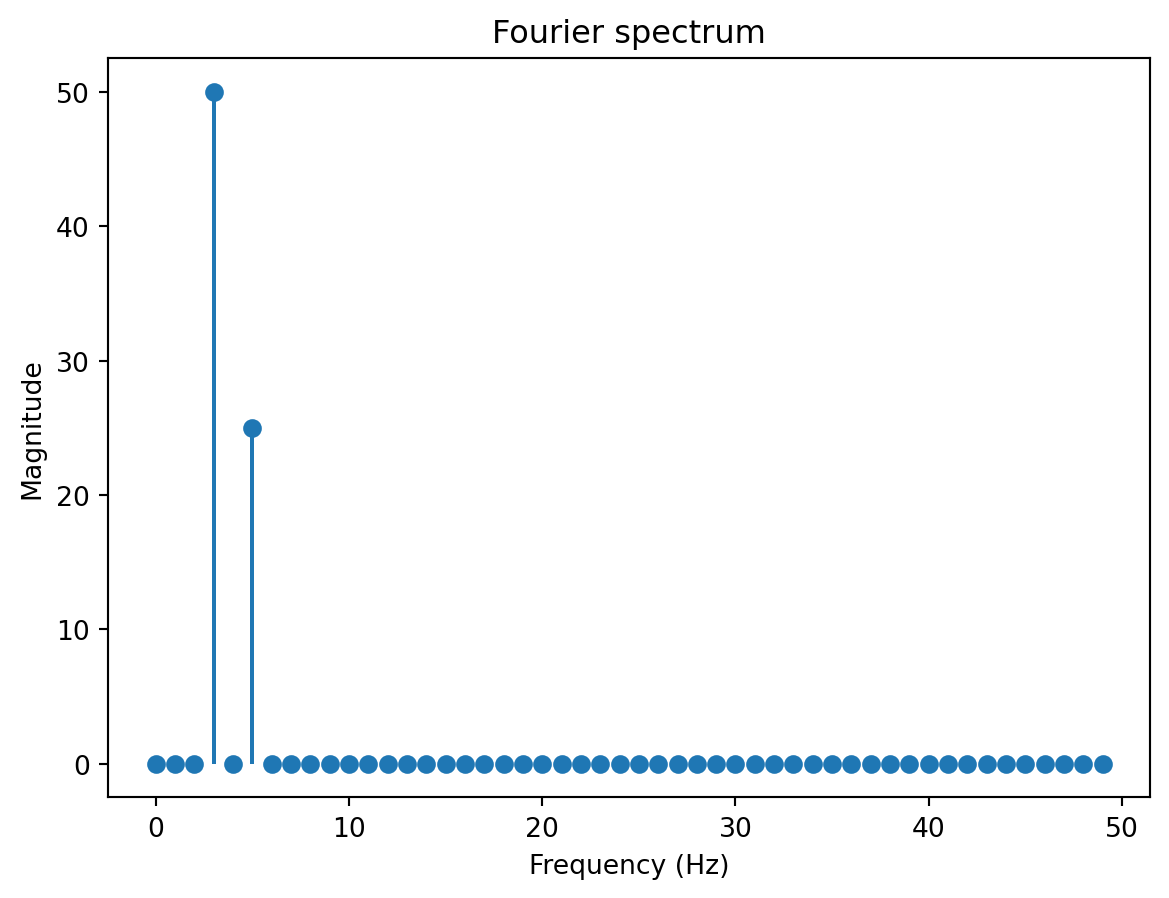

Peaks appear at 3Hz and 5Hz → the frequencies of the original signal.

3. Reconstruct signal using inverse FFT

signal_reconstructed = np.fft.ifft(X).real
print("Reconstruction error:", np.linalg.norm(signal - signal_reconstructed))

Reconstruction error: 1.4664679821708477e-15

Error is near zero → perfect reconstruction.

4. Orthogonality check of sinusoids

u = np.sin(2*np.pi*3*t)
v = np.sin(2*np.pi*5*t)

inner = np.dot(u, v)
print("Inner product of 3Hz and 5Hz sinusoids:", inner)

Inner product of 3Hz and 5Hz sinusoids: 1.2961853812498703e-14

The result is ≈ 0 → confirms orthogonality.

Try It Yourself

1. Change the frequencies to 7Hz and 9Hz. Do the Fourier peaks move accordingly?
2. Mix in some noise and check how the spectrum looks.
3. Try cosine signals instead of sine. Do you still see orthogonality?

The Takeaway

• Fourier analysis = linear algebra with orthogonal sinusoidal basis functions.
• Any signal can be decomposed into orthogonal waves.
• This orthogonal viewpoint powers audio, image compression, and signal processing.

80. Polynomial and Multifeature Least Squares (Fitting More Flexibly)

Least squares isn’t limited to straight lines. By adding polynomial or multiple features, we can fit curves and capture more complex relationships. This is the foundation of regression models in data science.

Formula Recap

Given data \((x_i, y_i)\), we build a design matrix \(A\):

• For polynomial fit of degree \(d\):

\[ A = \begin{bmatrix} 1 & x_1 & x_1^2 & \dots & x_1^d \\ 1 & x_2 & x_2^2 & \dots & x_2^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^d \end{bmatrix} \]

Then solve least squares:

\[ \hat{c} = \arg\min_c \|Ac - y\|^2 \]

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Generate noisy quadratic data

np.random.seed(0)
x = np.linspace(-3, 3, 30)
y_true = 1 - 2*x + 0.5*x**2
y_noisy = y_true + np.random.normal(scale=2.0, size=x.shape)

plt.scatter(x, y_noisy, label="Noisy data")
plt.plot(x, y_true, "g--", label="True curve")
plt.legend()
plt.show()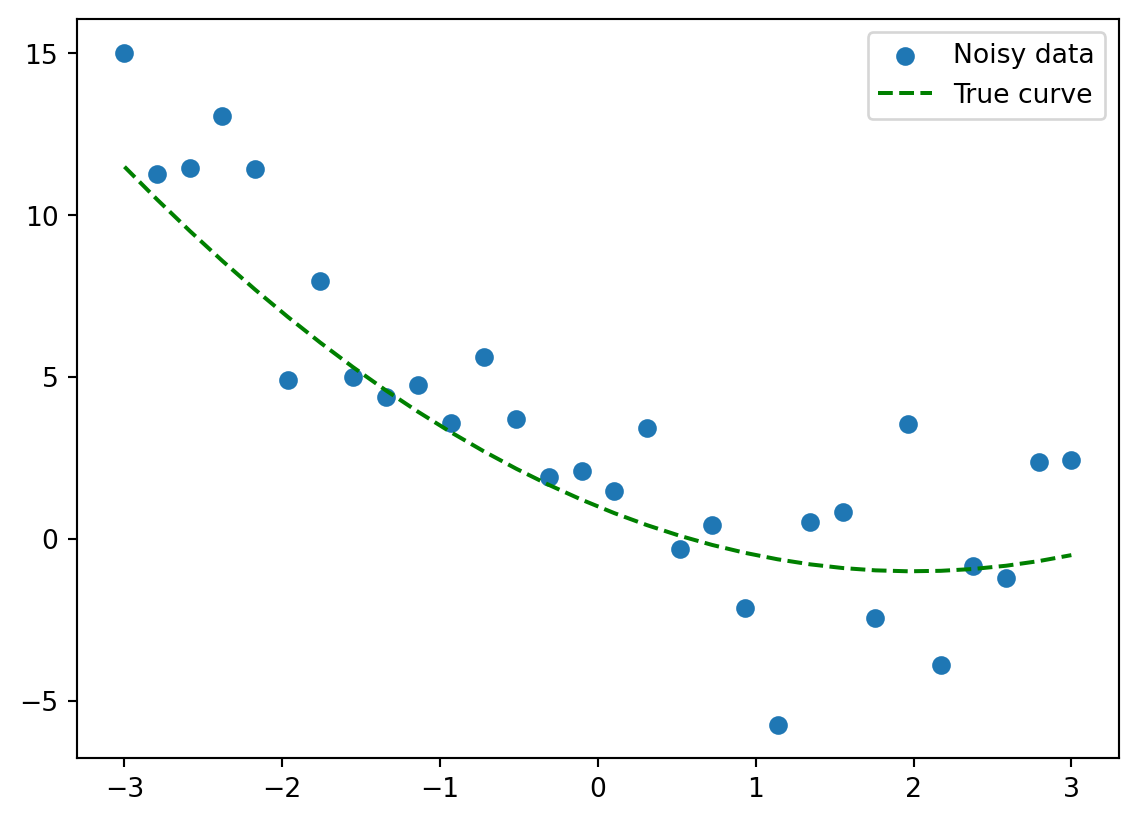

2. Build polynomial design matrix (degree 2)

A = np.column_stack([np.ones_like(x), x, x**2])
coeffs, *_ = np.linalg.lstsq(A, y_noisy, rcond=None)
print("Fitted coefficients:", coeffs)

Fitted coefficients: [ 1.15666306 -2.25753954  0.72733812]

3. Plot fitted polynomial

y_fit = A @ coeffs
plt.scatter(x, y_noisy, label="Noisy data")
plt.plot(x, y_fit, "r-", label="Fitted quadratic")
plt.legend()
plt.show()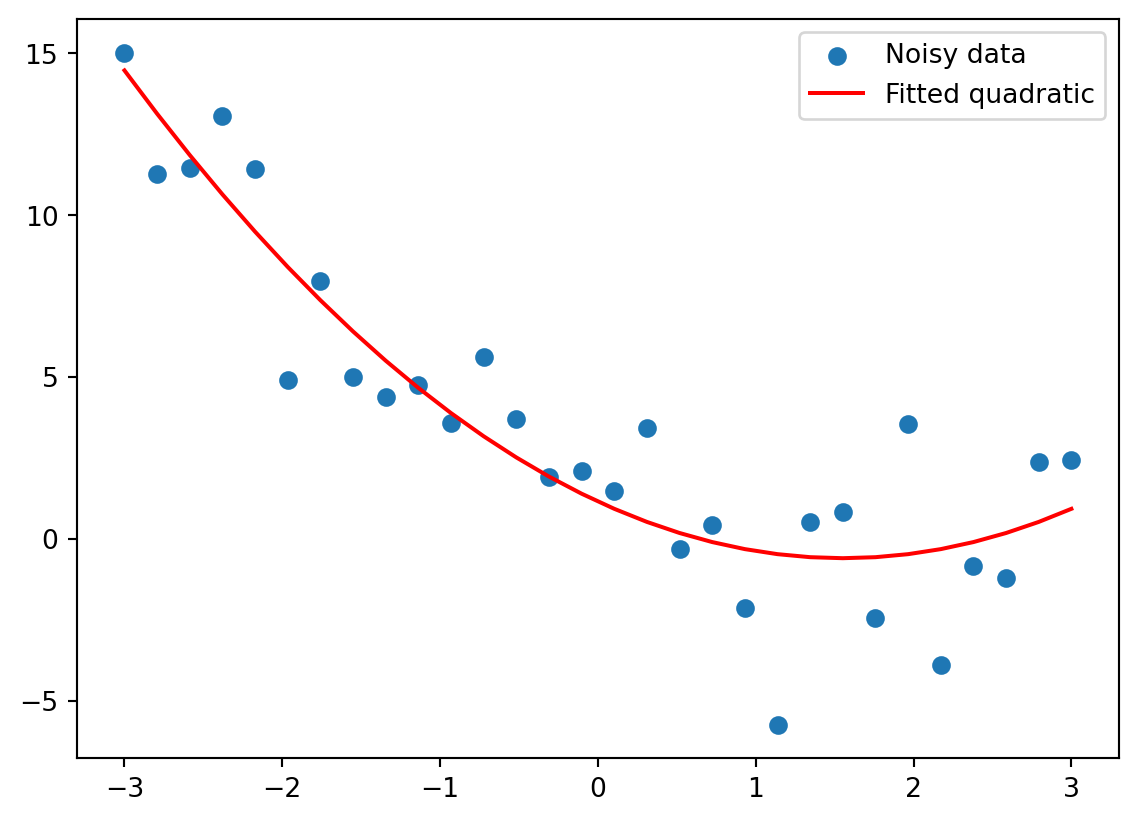

4. Higher-degree fit (overfitting demonstration)

A_high = np.column_stack([x**i for i in range(6)])  # degree 5
coeffs_high, *_ = np.linalg.lstsq(A_high, y_noisy, rcond=None)

y_fit_high = A_high @ coeffs_high
plt.scatter(x, y_noisy, label="Noisy data")
plt.plot(x, y_fit_high, "r-", label="Degree 5 polynomial")
plt.plot(x, y_true, "g--", label="True curve")
plt.legend()
plt.show()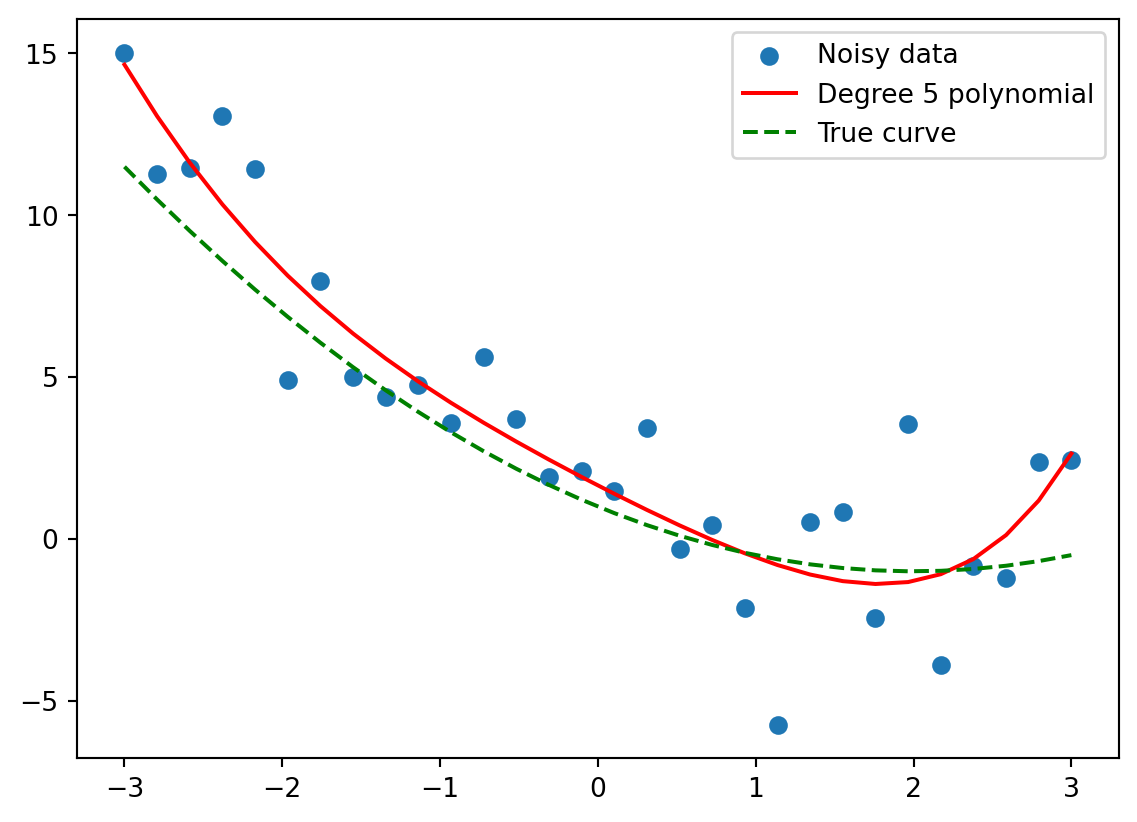

5. Multifeature regression example

Suppose we predict \(y\) from features \([x, x^2, \sin(x)]\):

A_multi = np.column_stack([np.ones_like(x), x, x**2, np.sin(x)])
coeffs_multi, *_ = np.linalg.lstsq(A_multi, y_noisy, rcond=None)
print("Multi-feature coefficients:", coeffs_multi)

Multi-feature coefficients: [ 1.15666306 -2.0492999   0.72733812 -0.65902274]

Try It Yourself

1. Fit degree 3, 4, 5 polynomials to the same data. Watch how the curve changes.
2. Add features like \(\cos(x)\) or \(\exp(x)\) - does the fit improve?
3. Compare training error (fit to noisy data) vs error on new test points.

The Takeaway

• Least squares can fit polynomials and arbitrary feature combinations.
• The design matrix encodes how input variables transform into features.
• This is the basis of regression, curve fitting, and many machine learning models.

Chapter 9. SVD, PCA, and Conditioning

81. Singular Values and SVD (Universal Factorization)

The Singular Value Decomposition (SVD) is one of the most powerful results in linear algebra. It says any \(m \times n\) matrix \(A\) can be factored as:

\[ A = U \Sigma V^T \]

• \(U\): orthogonal \(m \times m\) matrix (left singular vectors)
• \(\Sigma\): diagonal \(m \times n\) matrix with nonnegative numbers (singular values)
• \(V\): orthogonal \(n \times n\) matrix (right singular vectors)

Singular values are always nonnegative and sorted \(\sigma_1 \geq \sigma_2 \geq \dots\).

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Compute SVD of a matrix

A = np.array([[3,1,1],
              [-1,3,1]])

U, S, Vt = np.linalg.svd(A, full_matrices=True)

print("U:\n", U)
print("Singular values:", S)
print("V^T:\n", Vt)

U:
 [[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]
Singular values: [3.46410162 3.16227766]
V^T:
 [[-4.08248290e-01 -8.16496581e-01 -4.08248290e-01]
 [-8.94427191e-01  4.47213595e-01  5.27355937e-16]
 [-1.82574186e-01 -3.65148372e-01  9.12870929e-01]]

• U: orthogonal basis in input space.
• S: singular values (as a 1D array).
• V^T: orthogonal basis in output space.

2. Reconstruct \(A\) from decomposition

Sigma = np.zeros((U.shape[1], Vt.shape[0]))
Sigma[:len(S), :len(S)] = np.diag(S)

A_reconstructed = U @ Sigma @ Vt
print("Reconstruction error:", np.linalg.norm(A - A_reconstructed))

Reconstruction error: 1.5895974606912448e-15

The error should be near zero.

3. Rank from SVD

Number of nonzero singular values = rank of \(A\).

rank = np.sum(S > 1e-10)
print("Rank of A:", rank)

Rank of A: 2

4. Geometry: effect of \(A\)

SVD says:

1. \(V\) rotates input space.
2. \(\Sigma\) scales along orthogonal directions (by singular values).
3. \(U\) rotates to output space.

This explains why SVD works for any matrix (not just square ones).

5. Low-rank approximation preview

Keep only the top singular value(s) → best approximation of \(A\).

k = 1
A_approx = np.outer(U[:,0], Vt[0]) * S[0]
print("Rank-1 approximation:\n", A_approx)

Rank-1 approximation:
 [[1. 2. 1.]
 [1. 2. 1.]]

Try It Yourself

1. Compute SVD for a random 5×3 matrix. Check if \(U\) and \(V\) are orthogonal.
2. Compare singular values of a diagonal matrix vs a rotation matrix.
3. Zero out small singular values and see how much of \(A\) is preserved.

The Takeaway

• SVD factorizes any matrix into rotations and scalings.
• Singular values reveal rank and strength of directions.
• It’s the universal tool of numerical linear algebra: the backbone of PCA, compression, and stability analysis.

82. Geometry of SVD (Rotations + Stretching)

The Singular Value Decomposition (SVD) has a beautiful geometric interpretation: every matrix is just a combination of two rotations (or reflections) and a stretching.

For \(A = U \Sigma V^T\):

1. \(V^T\): rotates (or reflects) the input space.
2. \(\Sigma\): stretches space along orthogonal axes by singular values \(\sigma_i\).
3. \(U\): rotates (or reflects) the result into the output space.

This turns any linear transformation into a rotation → stretching → rotation pipeline.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Make a 2D matrix

A = np.array([[2, 1],
              [1, 3]])

2. Apply SVD

U, S, Vt = np.linalg.svd(A)

print("U:\n", U)
print("Singular values:", S)
print("V^T:\n", Vt)

U:
 [[-0.52573111 -0.85065081]
 [-0.85065081  0.52573111]]
Singular values: [3.61803399 1.38196601]
V^T:
 [[-0.52573111 -0.85065081]
 [-0.85065081  0.52573111]]

3. Visualize effect on the unit circle

The unit circle is often used to visualize linear transformations.

theta = np.linspace(0, 2*np.pi, 200)
circle = np.vstack((np.cos(theta), np.sin(theta)))

transformed = A @ circle

plt.plot(circle[0], circle[1], 'b--', label="Unit circle")
plt.plot(transformed[0], transformed[1], 'r-', label="Transformed")
plt.axis("equal")
plt.legend()
plt.title("Action of A on the unit circle")
plt.show()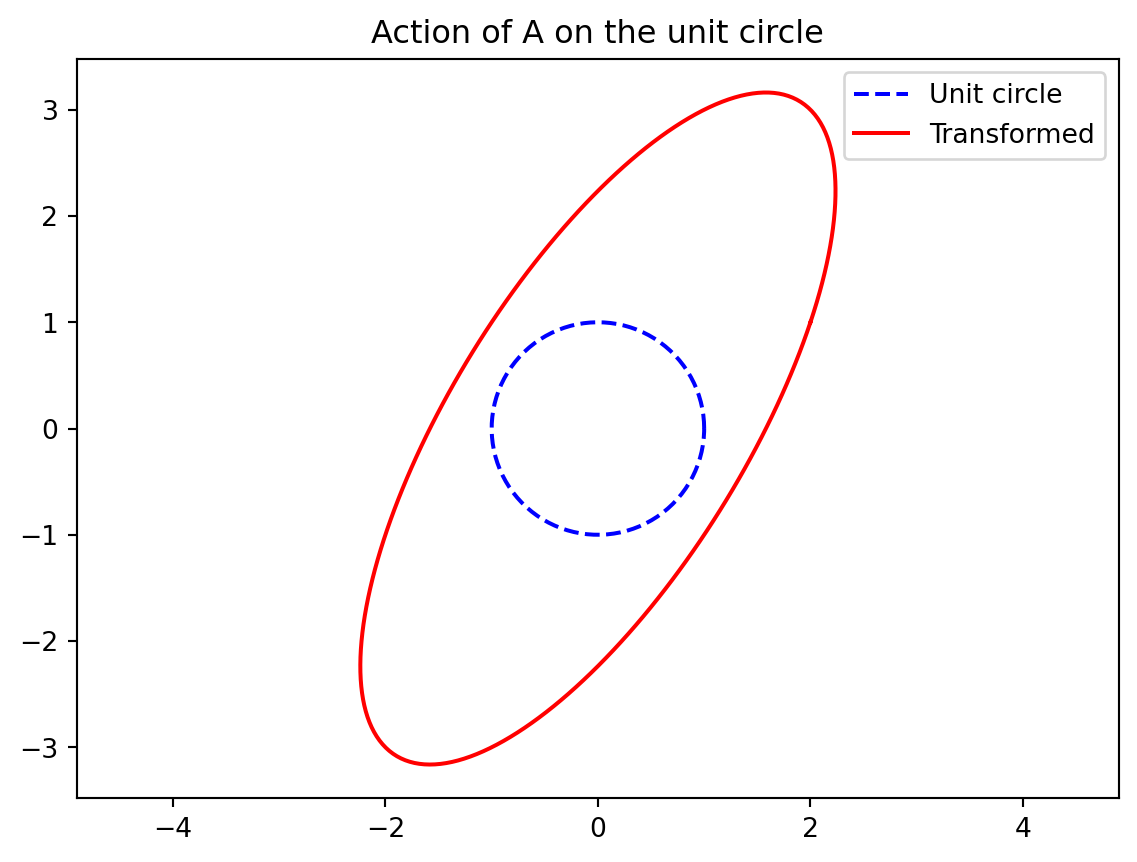

The circle becomes an ellipse. Its axes align with the singular vectors, and its radii are the singular values.

4. Compare with decomposition steps

# Apply V^T
step1 = Vt @ circle
# Apply Σ
Sigma = np.diag(S)
step2 = Sigma @ step1
# Apply U
step3 = U @ step2

plt.plot(circle[0], circle[1], 'b--', label="Unit circle")
plt.plot(step3[0], step3[1], 'g-', label="U Σ V^T circle")
plt.axis("equal")
plt.legend()
plt.title("SVD decomposition of transformation")
plt.show()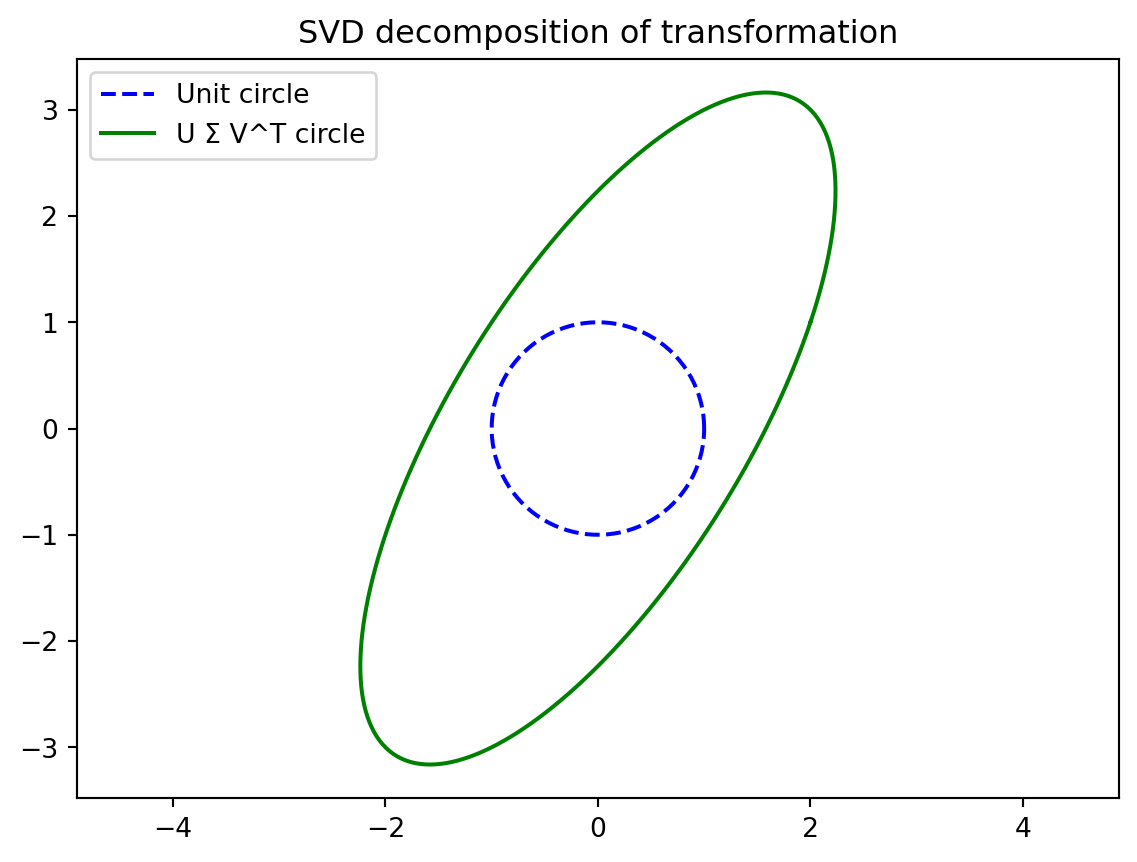

Both transformed shapes match → confirms SVD’s geometric picture.

Try It Yourself

1. Change \(A\) to a pure shear, like [[1,2],[0,1]]. How does the ellipse look?
2. Try a diagonal matrix, like [[3,0],[0,1]]. Do the singular vectors match the coordinate axes?
3. Scale the input circle to a square and see if geometry still works.

The Takeaway

• SVD = rotate → stretch → rotate.
• The unit circle becomes an ellipse: axes = singular vectors, radii = singular values.
• This geometric lens makes SVD intuitive and explains why it’s so widely used in data, graphics, and signal processing.

83. Relation to Eigen-Decompositions (ATA and AAT)

Singular values and eigenvalues are closely connected. While eigen-decomposition applies only to square matrices, SVD works for any rectangular matrix. The bridge between them is:

\[ A^T A v = \sigma^2 v \quad \text{and} \quad A A^T u = \sigma^2 u \]

• \(v\): right singular vector (from eigenvectors of \(A^T A\))
• \(u\): left singular vector (from eigenvectors of \(A A^T\))
• \(\sigma\): singular values (square roots of eigenvalues of \(A^T A\) or \(A A^T\))

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Define a rectangular matrix

A = np.array([[2, 0],
              [1, 1],
              [0, 1]])  # shape 3x2

2. Compute SVD directly

U, S, Vt = np.linalg.svd(A)
print("Singular values:", S)

Singular values: [2.30277564 1.30277564]

3. Compare with eigenvalues of \(A^T A\)

ATA = A.T @ A
eigvals, eigvecs = np.linalg.eig(ATA)

print("Eigenvalues of A^T A:", eigvals)
print("Square roots (sorted):", np.sqrt(np.sort(eigvals)[::-1]))

Eigenvalues of A^T A: [5.30277564 1.69722436]
Square roots (sorted): [2.30277564 1.30277564]

Notice: singular values from SVD = square roots of eigenvalues of \(A^T A\).

4. Compare with eigenvalues of \(A A^T\)

AAT = A @ A.T
eigvals2, eigvecs2 = np.linalg.eig(AAT)

print("Eigenvalues of A A^T:", eigvals2)
print("Square roots:", np.sqrt(np.sort(eigvals2)[::-1]))

Eigenvalues of A A^T: [ 5.30277564e+00  1.69722436e+00 -2.01266546e-17]
Square roots: [2.30277564 1.30277564        nan]

/var/folders/_g/lq_pglm508df70x751kkxrl80000gp/T/ipykernel_31637/436251338.py:5: RuntimeWarning: invalid value encountered in sqrt
  print("Square roots:", np.sqrt(np.sort(eigvals2)[::-1]))

They match too → confirming the relationship.

5. Verify singular vectors

• Right singular vectors (\(V\)) = eigenvectors of \(A^T A\).
• Left singular vectors (\(U\)) = eigenvectors of \(A A^T\).

print("Right singular vectors (V):\n", Vt.T)
print("Eigenvectors of A^T A:\n", eigvecs)

print("Left singular vectors (U):\n", U)
print("Eigenvectors of A A^T:\n", eigvecs2)

Right singular vectors (V):
 [[-0.95709203  0.28978415]
 [-0.28978415 -0.95709203]]
Eigenvectors of A^T A:
 [[ 0.95709203 -0.28978415]
 [ 0.28978415  0.95709203]]
Left singular vectors (U):
 [[-0.83125078  0.44487192  0.33333333]
 [-0.54146663 -0.51222011 -0.66666667]
 [-0.12584124 -0.73465607  0.66666667]]
Eigenvectors of A A^T:
 [[-0.83125078  0.44487192  0.33333333]
 [-0.54146663 -0.51222011 -0.66666667]
 [-0.12584124 -0.73465607  0.66666667]]

Try It Yourself

1. Try a square symmetric matrix and compare SVD with eigen-decomposition. Do they match?
2. For a tall vs wide rectangular matrix, check whether \(U\) and \(V\) differ.
3. Compute eigenvalues manually with np.linalg.eig for a random \(A\) and confirm singular values.

The Takeaway

• Singular values = square roots of eigenvalues of \(A^T A\) (or \(A A^T\)).
• Right singular vectors = eigenvectors of \(A^T A\).
• Left singular vectors = eigenvectors of \(A A^T\).
• SVD generalizes eigen-decomposition to all matrices, rectangular or square.

84. Low-Rank Approximation (Best Small Models)

One of the most useful applications of SVD is low-rank approximation: compressing a large matrix into a smaller one while keeping most of the important information.

The Eckart–Young theorem says: If \(A = U \Sigma V^T\), then the best rank-\(k\) approximation (in least-squares sense) is:

\[ A_k = U_k \Sigma_k V_k^T \]

where we keep only the top \(k\) singular values (and corresponding vectors).

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Create a matrix with hidden low-rank structure

np.random.seed(0)
U = np.random.randn(50, 5)   # 50 x 5
V = np.random.randn(5, 30)   # 5 x 30
A = U @ V  # true rank ≤ 5

2. Full SVD

U, S, Vt = np.linalg.svd(A, full_matrices=False)
print("Singular values:", S[:10])

Singular values: [4.90672194e+01 4.05935057e+01 3.39228766e+01 3.07883338e+01
 2.29261740e+01 3.97150036e-15 3.97150036e-15 3.97150036e-15
 3.97150036e-15 3.97150036e-15]

Only the first ~5 should be large; the rest close to zero.

3. Build rank-1 approximation

k = 1
A1 = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]
error1 = np.linalg.norm(A - A1)
print("Rank-1 approximation error:", error1)

Rank-1 approximation error: 65.36149641872869

4. Rank-5 approximation (should be almost exact)

k = 5
A5 = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]
error5 = np.linalg.norm(A - A5)
print("Rank-5 approximation error:", error5)

Rank-5 approximation error: 5.756573247253659e-14

5. Visual comparison (image compression demo)

Let’s see it on an image.

from sklearn.datasets import load_digits
digits = load_digits()
img = digits.images[0]  # 8x8 grayscale digit

U, S, Vt = np.linalg.svd(img, full_matrices=False)

# Keep only top 2 singular values
k = 2
img2 = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]

plt.subplot(1,2,1)
plt.imshow(img, cmap="gray")
plt.title("Original")

plt.subplot(1,2,2)
plt.imshow(img2, cmap="gray")
plt.title("Rank-2 Approximation")
plt.show()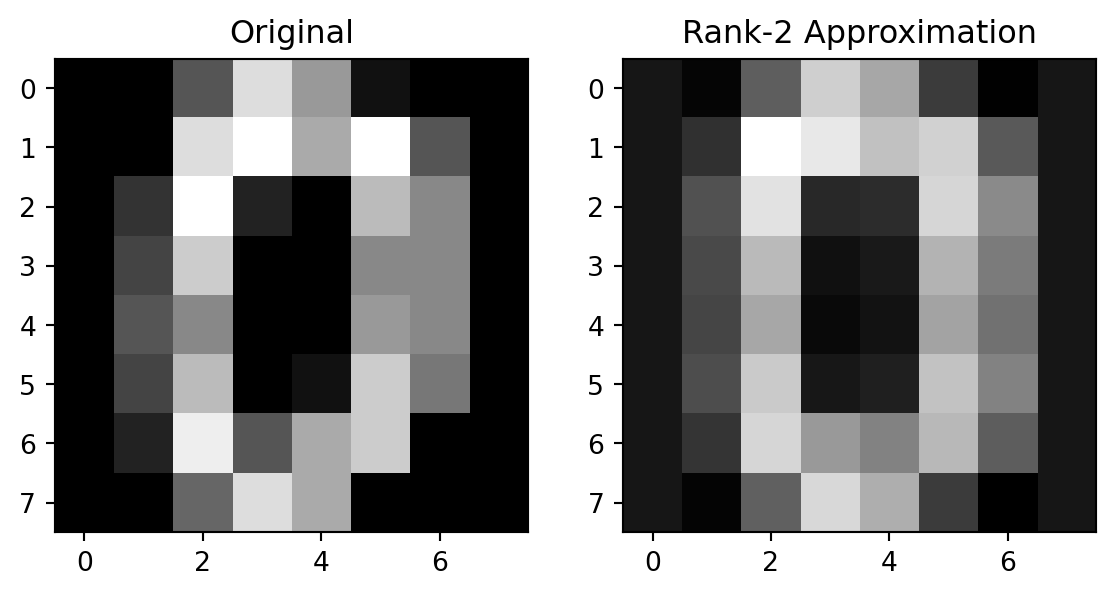

Even with just 2 singular values, the digit shape is recognizable.

Try It Yourself

1. Vary \(k\) in the image example (1, 2, 5, 10). How much detail do you keep?
2. Compare the approximation error \(\|A - A_k\|\) as \(k\) increases.
3. Apply low-rank approximation to random noisy data. Does it denoise?

The Takeaway

• SVD gives the best possible low-rank approximation in terms of error.
• By truncating singular values, you compress data while keeping its essential structure.
• This is the backbone of image compression, recommender systems, and dimensionality reduction.

85. Principal Component Analysis (Variance and Directions)

Principal Component Analysis (PCA) is one of the most important applications of SVD. It finds the directions (principal components) where data varies the most, and projects the data onto them to reduce dimensionality while preserving as much information as possible.

Mathematically:

1. Center the data (subtract the mean).
2. Compute covariance matrix \(C = \frac{1}{n} X^T X\).
3. Eigenvectors of \(C\) = principal directions.
4. Eigenvalues = variance explained.
5. Equivalently: PCA = SVD of centered data matrix.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

Step-by-Step Code Walkthrough

1. Generate synthetic 2D data

np.random.seed(0)
X = np.random.randn(200, 2) @ np.array([[3,1],[1,0.5]])  # stretched cloud

plt.scatter(X[:,0], X[:,1], alpha=0.3)
plt.title("Original data")
plt.axis("equal")
plt.show()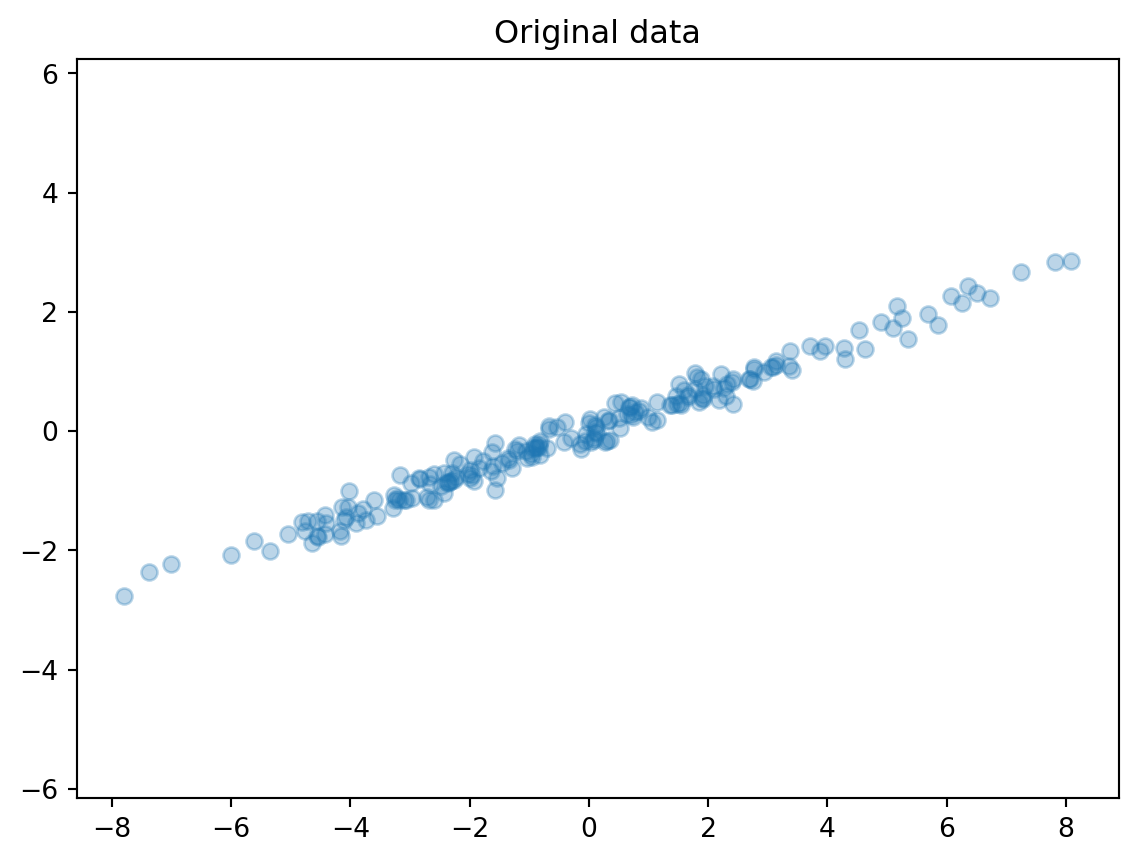

2. Center the data

X_centered = X - X.mean(axis=0)

3. Compute SVD

U, S, Vt = np.linalg.svd(X_centered, full_matrices=False)
print("Principal directions (V):\n", Vt)

Principal directions (V):
 [[-0.94430098 -0.32908307]
 [ 0.32908307 -0.94430098]]

Rows of Vt are the principal components.

4. Project data onto first component

X_pca1 = X_centered @ Vt.T[:,0]

plt.scatter(X_pca1, np.zeros_like(X_pca1), alpha=0.3)
plt.title("Data projected on first principal component")
plt.show()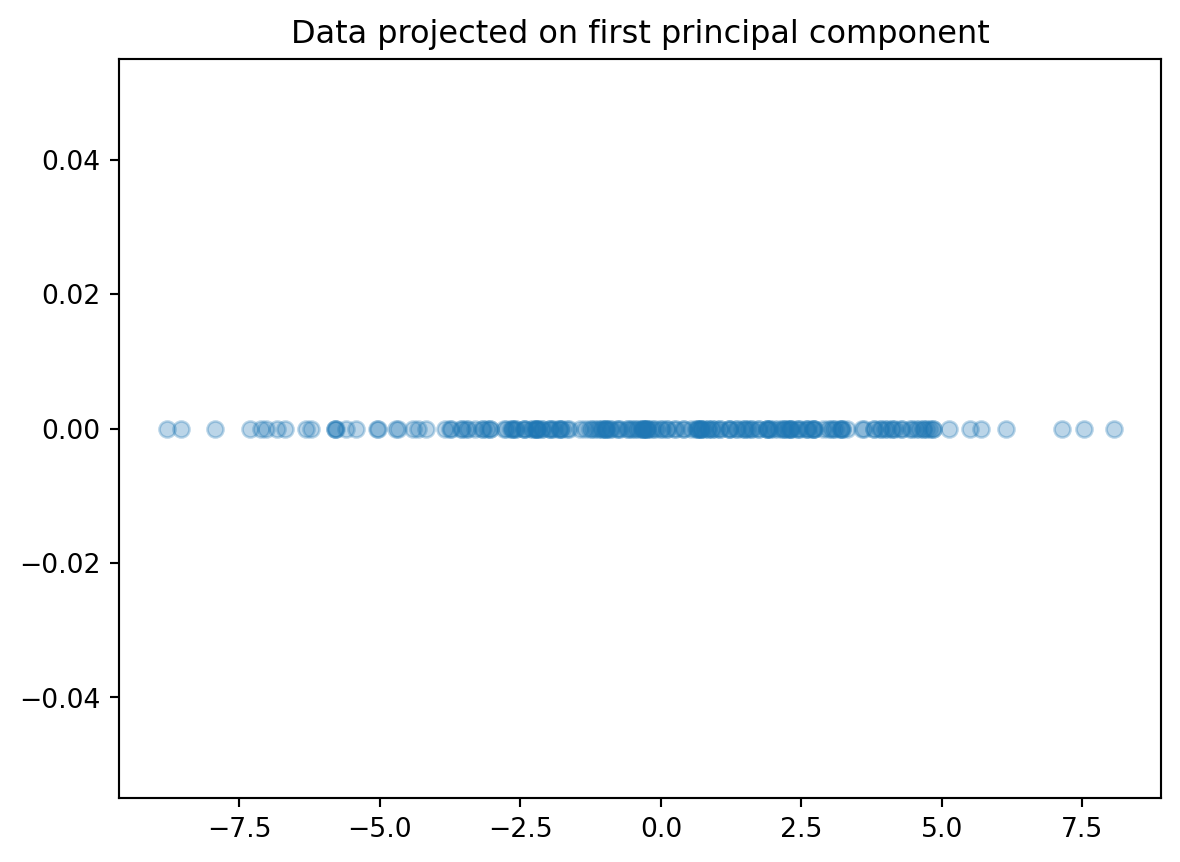

This collapses data into 1D, keeping the most variance.

5. Visualize principal axes

plt.scatter(X_centered[:,0], X_centered[:,1], alpha=0.3)
for length, vector in zip(S, Vt):
    plt.plot([0, vector[0]*length], [0, vector[1]*length], 'r-', linewidth=3)
plt.title("Principal components (directions of max variance)")
plt.axis("equal")
plt.show()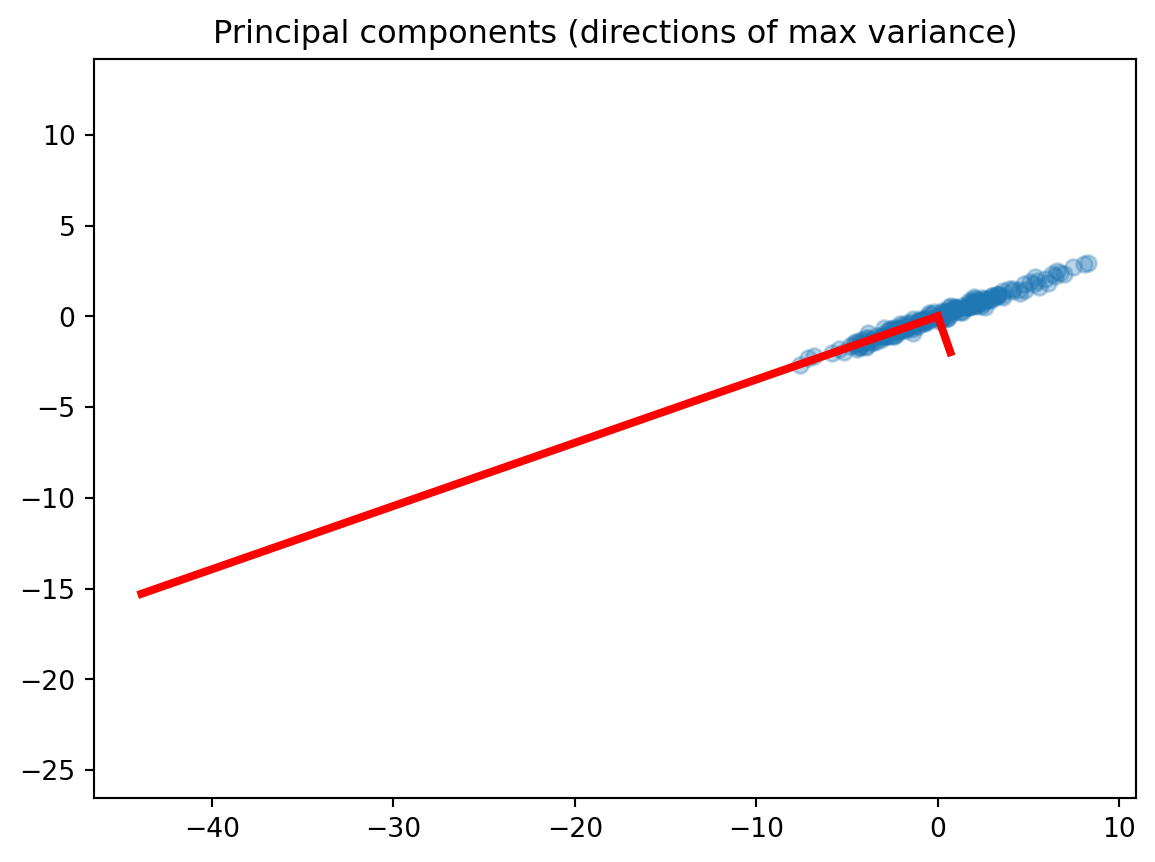

The red arrows show where the data spreads most.

6. PCA on real data (digits)

digits = load_digits()
X = digits.data  # 1797 samples, 64 features
X_centered = X - X.mean(axis=0)

U, S, Vt = np.linalg.svd(X_centered, full_matrices=False)

explained_variance = (S**2) / np.sum(S**2)
print("Explained variance ratio (first 5):", explained_variance[:5])

Explained variance ratio (first 5): [0.14890594 0.13618771 0.11794594 0.08409979 0.05782415]

Try It Yourself

1. Reduce digits dataset to 2D using the top 2 components and plot. Do digit clusters separate?
2. Compare explained variance ratio for top 10 components.
3. Add noise to data and check if PCA filters it out when projecting to fewer dimensions.

The Takeaway

• PCA finds directions of maximum variance using SVD.
• By projecting onto top components, you compress data with minimal information loss.
• PCA is the backbone of dimensionality reduction, visualization, and preprocessing in machine learning.

86. Pseudoinverse (Moore–Penrose) and Solving Ill-Posed Systems

The Moore–Penrose pseudoinverse \(A^+\) generalizes the inverse of a matrix. It allows solving systems \(Ax = b\) even when:

• \(A\) is not square, or
• \(A\) is singular (non-invertible).

The solution given by the pseudoinverse is the least-squares solution with minimum norm:

\[ x = A^+ b \]

If \(A = U \Sigma V^T\), then:

\[ A^+ = V \Sigma^+ U^T \]

where \(\Sigma^+\) is obtained by taking reciprocals of nonzero singular values.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Solve an overdetermined system (more equations than unknowns)

A = np.array([[1,1],
              [1,2],
              [1,3]])  # 3x2 system
b = np.array([1,2,2])

x_ls, *_ = np.linalg.lstsq(A, b, rcond=None)
print("Least-squares solution:", x_ls)

Least-squares solution: [0.66666667 0.5       ]

2. Compute with pseudoinverse

A_pinv = np.linalg.pinv(A)
x_pinv = A_pinv @ b
print("Pseudoinverse solution:", x_pinv)

Pseudoinverse solution: [0.66666667 0.5       ]

Both match → pseudoinverse gives least-squares solution.

3. Solve an underdetermined system (fewer equations than unknowns)

A = np.array([[1,2,3]])  # 1x3
b = np.array([1])

x_pinv = np.linalg.pinv(A) @ b
print("Minimum norm solution:", x_pinv)

Minimum norm solution: [0.07142857 0.14285714 0.21428571]

Here, infinitely many solutions exist. The pseudoinverse picks the one with smallest norm.

4. Compare with singular matrix

A = np.array([[1,2],
              [2,4]])  # rank deficient
b = np.array([1,2])

x_pinv = np.linalg.pinv(A) @ b
print("Solution with pseudoinverse:", x_pinv)

Solution with pseudoinverse: [0.2 0.4]

Even when \(A\) is singular, pseudoinverse provides a solution.

5. Manual pseudoinverse via SVD

A = np.array([[1,2],
              [3,4]])
U, S, Vt = np.linalg.svd(A)
S_inv = np.zeros((Vt.shape[0], U.shape[0]))
for i in range(len(S)):
    if S[i] > 1e-10:
        S_inv[i,i] = 1/S[i]

A_pinv_manual = Vt.T @ S_inv @ U.T
print("Manual pseudoinverse:\n", A_pinv_manual)
print("NumPy pseudoinverse:\n", np.linalg.pinv(A))

Manual pseudoinverse:
 [[-2.   1. ]
 [ 1.5 -0.5]]
NumPy pseudoinverse:
 [[-2.   1. ]
 [ 1.5 -0.5]]

They match.

Try It Yourself

1. Create an overdetermined system with noise and see how pseudoinverse smooths the solution.
2. Compare pseudoinverse with direct inverse (np.linalg.inv) on a square nonsingular matrix.
3. Zero out small singular values manually and see how solution changes.

The Takeaway

• The pseudoinverse solves any linear system, square or not.
• It provides the least-squares solution in overdetermined cases and the minimum-norm solution in underdetermined cases.
• Built on SVD, it is a cornerstone of regression, optimization, and numerical methods.

87. Conditioning and Sensitivity (How Errors Amplify)

Conditioning tells us how sensitive a system is to small changes. For a linear system \(Ax = b\):

• If \(A\) is well-conditioned, small changes in \(b\) or \(A\) → small changes in \(x\).
• If \(A\) is ill-conditioned, tiny changes can cause huge swings in \(x\).

The condition number is defined as:

\[ \kappa(A) = \|A\| \cdot \|A^{-1}\| \]

For SVD:

\[ \kappa(A) = \frac{\sigma_{\max}}{\sigma_{\min}} \]

where \(\sigma_{\max}\) and \(\sigma_{\min}\) are the largest and smallest singular values.

• Large \(\kappa(A)\) → unstable system.
• Small \(\kappa(A)\) → stable system.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Well-conditioned system

A = np.array([[2,0],
              [0,1]])
b = np.array([1,1])

x = np.linalg.solve(A, b)
cond = np.linalg.cond(A)
print("Solution:", x)
print("Condition number:", cond)

Solution: [0.5 1. ]
Condition number: 2.0

Condition number = ratio of singular values → moderate size.

2. Ill-conditioned system

A = np.array([[1, 1.0001],
              [1, 1.0000]])
b = np.array([2,2])

x = np.linalg.lstsq(A, b, rcond=None)[0]
cond = np.linalg.cond(A)
print("Solution:", x)
print("Condition number:", cond)

Solution: [ 2.00000000e+00 -5.73526099e-13]
Condition number: 40002.000075017124

Condition number is very large → instability.

3. Perturb the right-hand side

b2 = np.array([2, 2.001])  # tiny change
x2 = np.linalg.lstsq(A, b2, rcond=None)[0]
print("Solution after tiny change:", x2)

Solution after tiny change: [ 12.001 -10.   ]

The solution changes drastically → shows sensitivity.

4. Relation to singular values

U, S, Vt = np.linalg.svd(A)
print("Singular values:", S)
print("Condition number (SVD):", S[0]/S[-1])

Singular values: [2.000050e+00 4.999875e-05]
Condition number (SVD): 40002.00007501713

5. Scaling experiment

for scale in [1,1e-2,1e-4,1e-6]:
    A = np.array([[1,0],[0,scale]])
    print(f"Scale={scale}, condition number={np.linalg.cond(A)}")

Scale=1, condition number=1.0
Scale=0.01, condition number=100.0
Scale=0.0001, condition number=10000.0
Scale=1e-06, condition number=1000000.0

As scale shrinks, condition number explodes.

Try It Yourself

1. Generate random matrices and compute their condition numbers. Which are stable?
2. Compare condition numbers of Hilbert matrices (notoriously ill-conditioned).
3. Explore how rounding errors grow with high condition numbers.

The Takeaway

• Condition number = measure of problem sensitivity.
• \(\kappa(A) = \sigma_{\max}/\sigma_{\min}\).
• Ill-conditioned problems amplify errors and are numerically unstable → why scaling, regularization, and good formulations matter.

88. Matrix Norms and Singular Values (Measuring Size Properly)

Matrix norms measure the size or strength of a matrix. They extend the idea of vector length to matrices. Norms are crucial for analyzing stability, error growth, and performance of algorithms.

Some important norms:

• Frobenius norm:

\[ \|A\|_F = \sqrt{\sum_{i,j} |a_{ij}|^2} \]

Equivalent to treating the matrix as a big vector.

• Spectral norm (operator 2-norm):

\[ \|A\|_2 = \sigma_{\max} \]

The largest singular value - tells how much \(A\) can stretch a vector.

• 1-norm: maximum absolute column sum.
• ∞-norm: maximum absolute row sum.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Build a test matrix

A = np.array([[1, -2, 3],
              [0,  4, 5],
              [-1, 2, 1]])

2. Compute different norms

fro = np.linalg.norm(A, 'fro')
spec = np.linalg.norm(A, 2)
one_norm = np.linalg.norm(A, 1)
inf_norm = np.linalg.norm(A, np.inf)

print("Frobenius norm:", fro)
print("Spectral norm:", spec)
print("1-norm:", one_norm)
print("Infinity norm:", inf_norm)

Frobenius norm: 7.810249675906654
Spectral norm: 6.813953458914004
1-norm: 9.0
Infinity norm: 9.0

3. Compare spectral norm with largest singular value

U, S, Vt = np.linalg.svd(A)
print("Largest singular value:", S[0])
print("Spectral norm:", spec)

Largest singular value: 6.813953458914004
Spectral norm: 6.813953458914004

They match → spectral norm = largest singular value.

4. Frobenius norm from singular values

\[ \|A\|_F = \sqrt{\sigma_1^2 + \sigma_2^2 + \dots} \]

fro_from_svd = np.sqrt(np.sum(S**2))
print("Frobenius norm (from SVD):", fro_from_svd)

Frobenius norm (from SVD): 7.810249675906654

5. Stretching effect demonstration

Pick a random vector and see how much it grows:

x = np.random.randn(3)
stretch = np.linalg.norm(A @ x) / np.linalg.norm(x)
print("Stretch factor:", stretch)
print("Spectral norm (max possible stretch):", spec)

Stretch factor: 2.7537463268177698
Spectral norm (max possible stretch): 6.813953458914004

The stretch ≤ spectral norm, always.

Try It Yourself

1. Compare norms for diagonal matrices - do they match the largest diagonal entry?
2. Generate random matrices and see how norms differ.
3. Compute Frobenius vs spectral norm for a rank-1 matrix.

The Takeaway

• Frobenius norm = overall energy of the matrix.
• Spectral norm = maximum stretching power (largest singular value).
• Other norms (1-norm, ∞-norm) capture row/column dominance.
• Singular values unify all these views of “matrix size.”

89. Regularization (Ridge/Tikhonov to Tame Instability)

When solving \(Ax = b\), if \(A\) is ill-conditioned (large condition number), small errors in data can cause huge errors in the solution. Regularization stabilizes the problem by adding a penalty term that discourages extreme solutions.

The most common form: ridge regression (a.k.a. Tikhonov regularization):

\[ x_\lambda = \arg\min_x \|Ax - b\|^2 + \lambda \|x\|^2 \]

Closed form:

\[ x_\lambda = (A^T A + \lambda I)^{-1} A^T b \]

Here \(\lambda > 0\) controls the amount of regularization:

• Small \(\lambda\): solution close to least-squares.
• Large \(\lambda\): smaller coefficients, more stability.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Build an ill-conditioned system

A = np.array([[1, 1.001],
              [1, 0.999]])
b = np.array([2, 2])

2. Solve without regularization

x_ls, *_ = np.linalg.lstsq(A, b, rcond=None)
print("Least squares solution:", x_ls)

Least squares solution: [ 2.00000000e+00 -2.84186735e-14]

The result may be unstable.

3. Apply ridge regularization

lam = 0.1
x_ridge = np.linalg.inv(A.T @ A + lam*np.eye(2)) @ A.T @ b
print("Ridge solution (λ=0.1):", x_ridge)

Ridge solution (λ=0.1): [0.97561927 0.97559976]

4. Compare effect of different λ

lambdas = np.logspace(-4, 2, 20)
solutions = []
for lam in lambdas:
    x_reg = np.linalg.inv(A.T @ A + lam*np.eye(2)) @ A.T @ b
    solutions.append(np.linalg.norm(x_reg))

plt.semilogx(lambdas, solutions, 'o-')
plt.xlabel("λ (regularization strength)")
plt.ylabel("Solution norm")
plt.title("Effect of ridge regularization")
plt.show()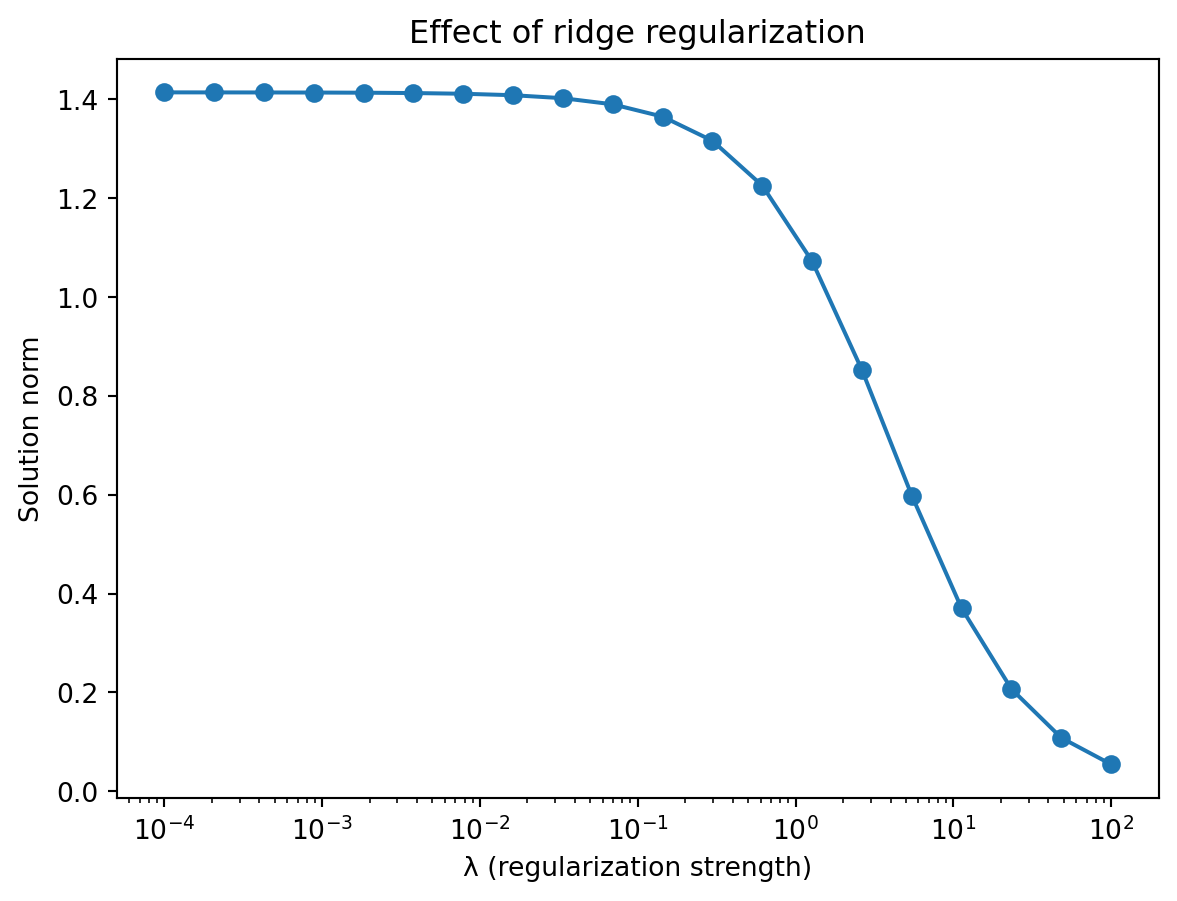

As \(\lambda\) increases, the solution becomes smaller and more stable.

5. Connection to SVD

If \(A = U \Sigma V^T\):

\[ x_\lambda = \sum_i \frac{\sigma_i}{\sigma_i^2 + \lambda} (u_i^T b) v_i \]

Small singular values (causing instability) get damped by \(\frac{\sigma_i}{\sigma_i^2 + \lambda}\).

Try It Yourself

1. Experiment with larger and smaller \(\lambda\). What happens to the solution?
2. Add random noise to \(b\). Compare least-squares vs ridge stability.
3. Plot how each coefficient changes with λ.

The Takeaway

• Regularization controls instability in ill-conditioned problems.
• Ridge regression balances fit vs. stability using λ.
• In SVD terms, regularization damps small singular values that cause wild solutions.

90. Rank-Revealing QR and Practical Diagnostics (What Rank Really Is)

In practice, we often need to determine the numerical rank of a matrix - not just the theoretical rank, but how many directions carry meaningful information beyond round-off errors or noise. A useful tool for this is the Rank-Revealing QR (RRQR) factorization.

For a matrix \(A\):

\[ A P = Q R \]

• \(Q\): orthogonal matrix
• \(R\): upper triangular matrix
• \(P\): column permutation matrix

By reordering columns smartly, the diagonal of \(R\) reveals which directions are significant.

Set Up Your Lab

import numpy as np
from scipy.linalg import qr

Step-by-Step Code Walkthrough

1. Build a nearly rank-deficient matrix

A = np.array([[1, 2, 3],
              [2, 4.001, 6],
              [3, 6, 9.001]])
print("Rank (theoretical):", np.linalg.matrix_rank(A))

Rank (theoretical): 3

This matrix is almost rank 2 but with small perturbations.

2. QR with column pivoting

Q, R, P = qr(A, pivoting=True)
print("R:\n", R)
print("Column permutation:", P)

R:
 [[-1.12257740e+01 -7.48384925e+00 -3.74165738e+00]
 [ 0.00000000e+00 -1.20185042e-03 -1.84886859e-04]
 [ 0.00000000e+00  0.00000000e+00 -7.41196374e-05]]
Column permutation: [2 1 0]

The diagonal entries of \(R\) decrease rapidly → numerical rank is determined where they become tiny.

3. Compare with SVD

U, S, Vt = np.linalg.svd(A)
print("Singular values:", S)

Singular values: [1.40009286e+01 1.00000000e-03 7.14238341e-05]

The singular values tell the same story: one is very small → effective rank ≈ 2.

4. Thresholding for rank

tol = 1e-3
rank_est = np.sum(S > tol)
print("Estimated rank:", rank_est)

Estimated rank: 2

5. Diagnostics on a noisy matrix

np.random.seed(0)
B = np.random.randn(50, 10) @ np.random.randn(10, 10)  # rank ≤ 10
B[:, -1] += 1e-6 * np.random.randn(50)  # tiny noise

U, S, Vt = np.linalg.svd(B)
plt.semilogy(S, 'o-')
plt.title("Singular values (log scale)")
plt.xlabel("Index")
plt.ylabel("Value")
plt.show()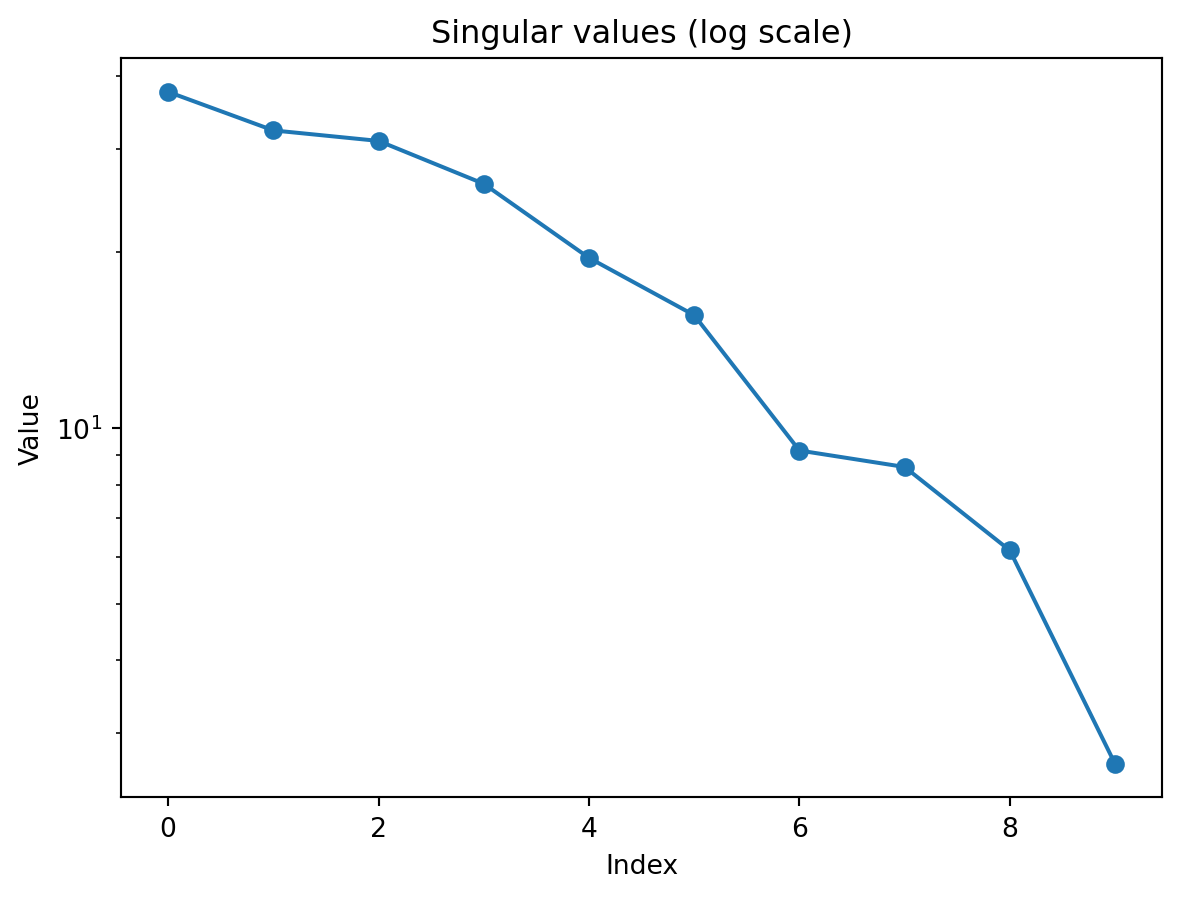

The drop in singular values shows effective rank.

Try It Yourself

1. Change the perturbation in \(A\) from 0.001 to 0.000001. Does the numerical rank change?
2. Test QR with pivoting on random rectangular matrices.
3. Compare rank estimates from QR vs SVD for large noisy matrices.

The Takeaway

• Rank-revealing QR is a practical tool to detect effective rank in real-world data.
• SVD gives the most precise picture (singular values), but QR with pivoting is faster.
• Understanding numerical rank is crucial for diagnostics, stability, and model complexity control.

Chapter 10. Applications and computation

91. 2D/3D Geometry Pipelines (Cameras, Rotations, and Transforms)

Linear algebra powers the geometry pipelines in computer graphics and robotics.

• 2D transforms: rotation, scaling, translation.
• 3D transforms: same ideas, but with an extra dimension.
• Homogeneous coordinates let us unify all transforms (even translations) into matrix multiplications.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Rotation in 2D

\[ R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \]

theta = np.pi/4  # 45 degrees
R = np.array([[np.cos(theta), -np.sin(theta)],
              [np.sin(theta),  np.cos(theta)]])

point = np.array([1, 0])
rotated = R @ point

print("Original:", point)
print("Rotated:", rotated)

Original: [1 0]
Rotated: [0.70710678 0.70710678]

2. Translation using homogeneous coordinates

In 2D:

\[ T(dx, dy) = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} \]

T = np.array([[1,0,2],
              [0,1,1],
              [0,0,1]])

p_h = np.array([1,1,1])  # homogeneous (x=1,y=1)
translated = T @ p_h
print("Translated point:", translated)

Translated point: [3 2 1]

3. Combine rotation + translation

Transformations compose by multiplying matrices.

M = T @ np.block([[R, np.zeros((2,1))],
                  [np.zeros((1,2)), 1]])
combined = M @ p_h
print("Combined transform (rotation+translation):", combined)

Combined transform (rotation+translation): [2.         2.41421356 1.        ]

4. 3D rotation (around z-axis)

\[ R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

theta = np.pi/3
Rz = np.array([[np.cos(theta), -np.sin(theta), 0],
               [np.sin(theta),  np.cos(theta), 0],
               [0,              0,             1]])

point3d = np.array([1,0,0])
rotated3d = Rz @ point3d
print("3D rotated point:", rotated3d)

3D rotated point: [0.5       0.8660254 0.       ]

5. Camera projection (3D → 2D)

Simple pinhole model:

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} f \cdot x / z \\ f \cdot y / z \end{bmatrix} \]

f = 1.0  # focal length
P = np.array([[f,0,0],
              [0,f,0],
              [0,0,1]])  # projection matrix

point3d = np.array([2,3,5])
p_proj = P @ point3d
p_proj = p_proj[:2] / p_proj[2]  # divide by z
print("Projected 2D point:", p_proj)

Projected 2D point: [0.4 0.6]

Try It Yourself

1. Rotate a square in 2D, then translate it. Plot before/after.
2. Rotate a 3D point cloud around x, y, and z axes.
3. Project a cube into 2D using the pinhole camera model.

The Takeaway

• Geometry pipelines = sequences of linear transforms.
• Homogeneous coordinates unify rotation, scaling, and translation.
• Camera projection links 3D world to 2D images - a cornerstone of graphics and vision.

92. Computer Graphics and Robotics (Homogeneous Tricks in Action)

Computer graphics and robotics both rely on homogeneous coordinates to unify rotations, translations, scalings, and projections into a single framework. With \(4 \times 4\) matrices in 3D, entire transformation pipelines can be built as matrix products.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Homogeneous representation of a point

In 3D:

\[ (x, y, z) \mapsto (x, y, z, 1) \]

p = np.array([1,2,3,1])  # homogeneous point

2. Define translation, rotation, and scaling matrices

• Translation by \((dx,dy,dz)\):

T = np.array([[1,0,0,2],
              [0,1,0,1],
              [0,0,1,3],
              [0,0,0,1]])

• Scaling by factors \((sx, sy, sz)\):

S = np.diag([2, 0.5, 1.5, 1])

• Rotation about z-axis (\(\theta = 90^\circ\)):

theta = np.pi/2
Rz = np.array([[np.cos(theta), -np.sin(theta), 0, 0],
               [np.sin(theta),  np.cos(theta), 0, 0],
               [0,              0,             1, 0],
               [0,              0,             0, 1]])

3. Combine transforms into a pipeline

M = T @ Rz @ S  # first scale, then rotate, then translate
p_transformed = M @ p
print("Transformed point:", p_transformed)

Transformed point: [1.  3.  7.5 1. ]

4. Robotics: forward kinematics of a 2-link arm

Each joint is a rotation + translation.

def link(theta, length):
    return np.array([[np.cos(theta), -np.sin(theta), 0, length*np.cos(theta)],
                     [np.sin(theta),  np.cos(theta), 0, length*np.sin(theta)],
                     [0,              0,             1, 0],
                     [0,              0,             0, 1]])

theta1, theta2 = np.pi/4, np.pi/6
L1, L2 = 2, 1.5

M1 = link(theta1, L1)
M2 = link(theta2, L2)

end_effector = M1 @ M2 @ np.array([0,0,0,1])
print("End effector position:", end_effector[:3])

End effector position: [1.80244213 2.8631023  0.        ]

5. Graphics: simple 3D camera projection

f = 2.0
P = np.array([[f,0,0,0],
              [0,f,0,0],
              [0,0,1,0]])

cube = np.array([[x,y,z,1] for x in [0,1] for y in [0,1] for z in [0,1]])
proj = (P @ cube.T).T
proj2d = proj[:,:2] / proj[:,2:3]

plt.scatter(proj2d[:,0], proj2d[:,1])
plt.title("Projected cube")
plt.show()

/var/folders/_g/lq_pglm508df70x751kkxrl80000gp/T/ipykernel_31637/2038614107.py:8: RuntimeWarning: divide by zero encountered in divide
  proj2d = proj[:,:2] / proj[:,2:3]
/var/folders/_g/lq_pglm508df70x751kkxrl80000gp/T/ipykernel_31637/2038614107.py:8: RuntimeWarning: invalid value encountered in divide
  proj2d = proj[:,:2] / proj[:,2:3]

Try It Yourself

1. Change order of transforms (Rz @ S @ T). How does the result differ?
2. Add a third joint to the robotic arm and compute new end-effector position.
3. Project the cube with different focal lengths \(f\).

The Takeaway

• Homogeneous coordinates unify all transformations.
• Robotics uses this framework for forward kinematics.
• Graphics uses it for camera and projection pipelines.
• Both fields rely on the same linear algebra tricks - just applied differently.

93. Graphs, Adjacency, and Laplacians (Networks via Matrices)

Graphs can be studied with linear algebra by encoding them into matrices. Two of the most important:

• Adjacency matrix \(A\):

  \[ A_{ij} = \begin{cases} 1 & \text{if edge between i and j exists} \\ 0 & \text{otherwise} \end{cases} \]

• Graph Laplacian \(L\):

  \[ L = D - A \]

  where \(D\) is the degree matrix ($D_{ii} = $ number of neighbors of node \(i\)).

These matrices let us analyze connectivity, diffusion, and clustering.

Set Up Your Lab

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Build a simple graph

G = nx.Graph()
G.add_edges_from([(0,1), (1,2), (2,3), (3,0), (0,2)])  # square with diagonal

nx.draw(G, with_labels=True, node_color="lightblue", node_size=800)
plt.show()

2. Adjacency matrix

A = nx.to_numpy_array(G)
print("Adjacency matrix:\n", A)

Adjacency matrix:
 [[0. 1. 1. 1.]
 [1. 0. 1. 0.]
 [1. 1. 0. 1.]
 [1. 0. 1. 0.]]

3. Degree and Laplacian matrices

D = np.diag(A.sum(axis=1))
L = D - A
print("Degree matrix:\n", D)
print("Graph Laplacian:\n", L)

Degree matrix:
 [[3. 0. 0. 0.]
 [0. 2. 0. 0.]
 [0. 0. 3. 0.]
 [0. 0. 0. 2.]]
Graph Laplacian:
 [[ 3. -1. -1. -1.]
 [-1.  2. -1.  0.]
 [-1. -1.  3. -1.]
 [-1.  0. -1.  2.]]

4. Eigenvalues of Laplacian (connectivity check)

eigvals, eigvecs = np.linalg.eigh(L)
print("Laplacian eigenvalues:", eigvals)

Laplacian eigenvalues: [1.11022302e-16 2.00000000e+00 4.00000000e+00 4.00000000e+00]

• The number of zero eigenvalues = number of connected components.

5. Spectral embedding (clustering)

Use Laplacian eigenvectors to embed nodes in low dimensions.

coords = eigvecs[:,1:3]  # skip the trivial first eigenvector
plt.scatter(coords[:,0], coords[:,1], c=range(len(coords)), cmap="tab10", s=200)
for i, (x,y) in enumerate(coords):
    plt.text(x, y, str(i), fontsize=12, ha="center", va="center", color="white")
plt.title("Spectral embedding of graph")
plt.show()

Try It Yourself

1. Remove one edge from the graph and see how Laplacian eigenvalues change.
2. Add a disconnected node - does an extra zero eigenvalue appear?
3. Try a random graph and compare adjacency vs Laplacian spectra.

The Takeaway

• Adjacency matrices describe direct graph structure.
• Laplacians capture connectivity and diffusion.
• Eigenvalues of \(L\) reveal graph properties like connectedness and clustering - bridging networks with linear algebra.

94. Data Preprocessing as Linear Ops (Centering, Whitening, Scaling)

Many machine learning and data analysis workflows begin with preprocessing, and linear algebra provides the tools.

• Centering: subtract the mean → move data to origin.
• Scaling: divide by standard deviation → normalize feature ranges.
• Whitening: decorrelate features → make covariance matrix the identity.

Each step can be written as a matrix operation.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Generate correlated data

np.random.seed(0)
X = np.random.randn(200, 2) @ np.array([[3,1],[1,0.5]])
plt.scatter(X[:,0], X[:,1], alpha=0.4)
plt.title("Original correlated data")
plt.axis("equal")
plt.show()

2. Centering (subtract mean)

X_centered = X - X.mean(axis=0)
print("Mean after centering:", X_centered.mean(axis=0))

Mean after centering: [ 8.88178420e-18 -1.22124533e-17]

3. Scaling (normalize features)

X_scaled = X_centered / X_centered.std(axis=0)
print("Std after scaling:", X_scaled.std(axis=0))

Std after scaling: [1. 1.]

4. Whitening via eigen-decomposition

Covariance of centered data:

C = np.cov(X_centered.T)
eigvals, eigvecs = np.linalg.eigh(C)

W = eigvecs @ np.diag(1/np.sqrt(eigvals)) @ eigvecs.T
X_white = X_centered @ W

Check covariance:

print("Whitened covariance:\n", np.cov(X_white.T))

Whitened covariance:
 [[1.00000000e+00 2.54402864e-15]
 [2.54402864e-15 1.00000000e+00]]

5. Compare scatter plots

plt.subplot(1,3,1)
plt.scatter(X[:,0], X[:,1], alpha=0.4)
plt.title("Original")

plt.subplot(1,3,2)
plt.scatter(X_scaled[:,0], X_scaled[:,1], alpha=0.4)
plt.title("Scaled")

plt.subplot(1,3,3)
plt.scatter(X_white[:,0], X_white[:,1], alpha=0.4)
plt.title("Whitened")

plt.tight_layout()
plt.show()

• Original: elongated ellipse.
• Scaled: axis-aligned ellipse.
• Whitened: circular cloud (uncorrelated, unit variance).

Try It Yourself

1. Add a third feature and apply centering, scaling, whitening.
2. Compare whitening with PCA - they use the same eigen-decomposition.
3. Test what happens if you skip centering before whitening.

The Takeaway

• Centering → mean zero.
• Scaling → unit variance.
• Whitening → features uncorrelated, variance = 1. Linear algebra provides the exact matrix operations to make preprocessing systematic and reliable.

95. Linear Regression and Classification (From Model to Matrix)

Linear regression and classification problems can be written neatly in matrix form. This unifies data, models, and solutions under the framework of least squares and linear decision boundaries.

Linear Regression Model

For data \((x_i, y_i)\):

\[ y \approx X \beta \]

• \(X\): design matrix (rows = samples, columns = features).
• \(\beta\): coefficients to solve for.
• Solution (least squares):

\[ \hat{\beta} = (X^T X)^{-1} X^T y \]

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification

Step-by-Step Code Walkthrough

1. Linear regression example

np.random.seed(0)
X = np.linspace(0, 10, 30).reshape(-1,1)
y = 3*X.squeeze() + 5 + np.random.randn(30)*2

Construct design matrix with bias term:

X_design = np.column_stack([np.ones_like(X), X])
beta_hat, *_ = np.linalg.lstsq(X_design, y, rcond=None)
print("Fitted coefficients:", beta_hat)

Fitted coefficients: [6.65833151 2.84547628]

2. Visualize regression line

y_pred = X_design @ beta_hat

plt.scatter(X, y, label="Data")
plt.plot(X, y_pred, 'r-', label="Fitted line")
plt.legend()
plt.show()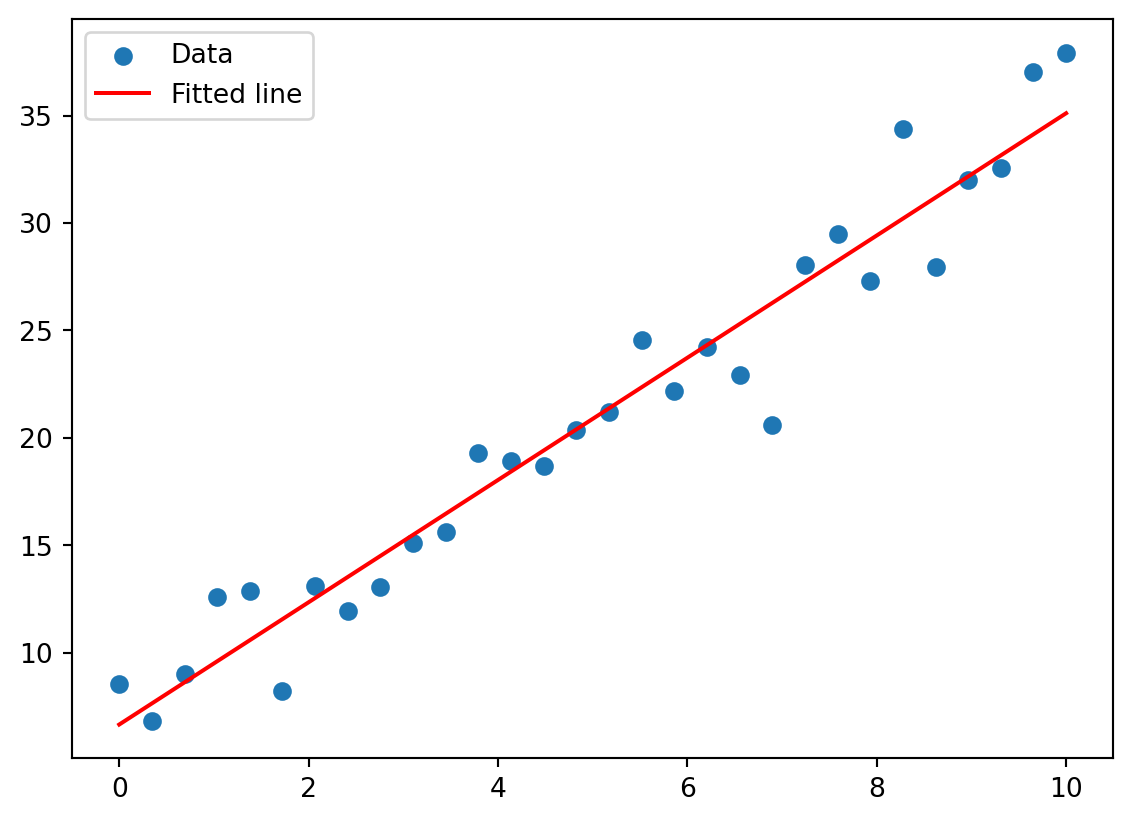

3. Logistic classification with linear decision boundary

Xc, yc = make_classification(n_features=2, n_redundant=0, n_informative=2,
                             n_clusters_per_class=1, n_samples=100, random_state=0)

plt.scatter(Xc[:,0], Xc[:,1], c=yc, cmap="bwr", alpha=0.7)
plt.title("Classification data")
plt.show()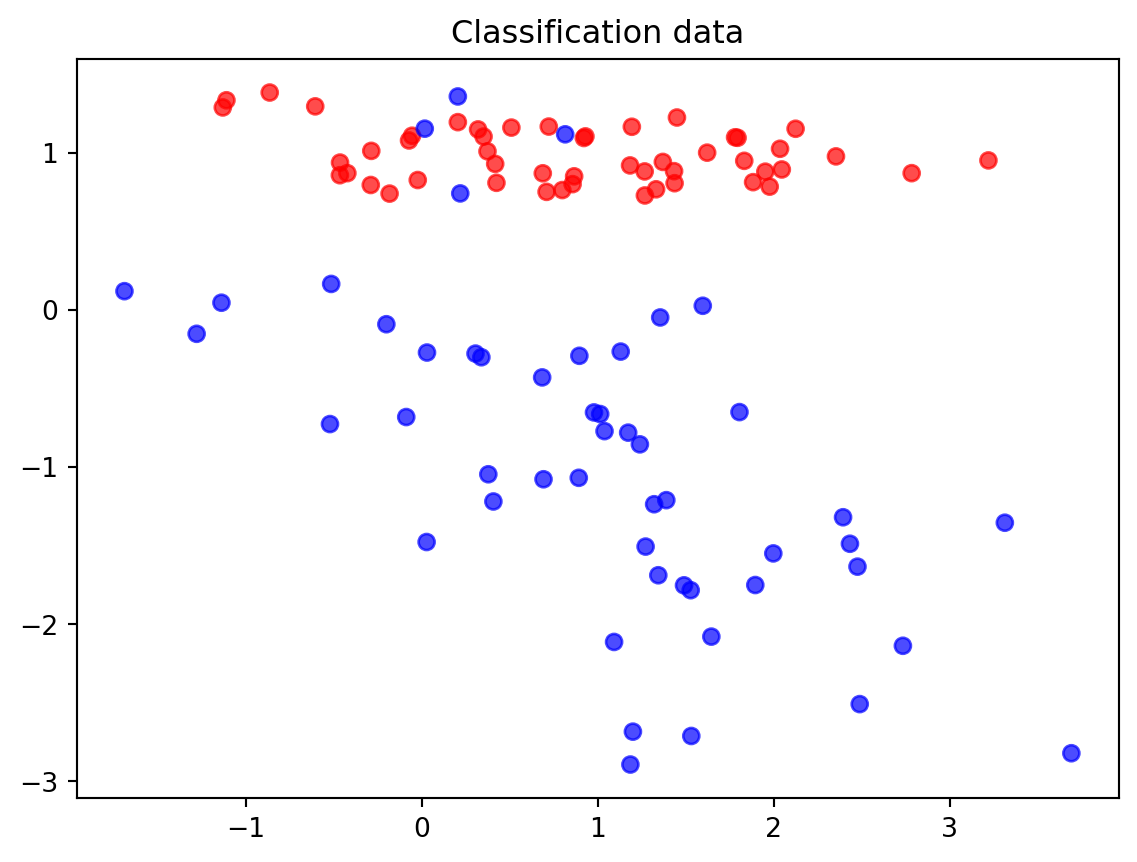

4. Logistic regression via gradient descent

def sigmoid(z):
    return 1/(1+np.exp(-z))

X_design = np.column_stack([np.ones(len(Xc)), Xc])
y = yc

w = np.zeros(X_design.shape[1])
lr = 0.1

for _ in range(2000):
    preds = sigmoid(X_design @ w)
    grad = X_design.T @ (preds - y) / len(y)
    w -= lr * grad

print("Learned weights:", w)

Learned weights: [-2.10451116  0.70752542  4.13295129]

5. Plot decision boundary

xx, yy = np.meshgrid(np.linspace(Xc[:,0].min()-1, Xc[:,0].max()+1, 200),
                     np.linspace(Xc[:,1].min()-1, Xc[:,1].max()+1, 200))

grid = np.c_[np.ones(xx.size), xx.ravel(), yy.ravel()]
probs = sigmoid(grid @ w).reshape(xx.shape)

plt.contourf(xx, yy, probs, levels=[0,0.5,1], alpha=0.3, cmap="bwr")
plt.scatter(Xc[:,0], Xc[:,1], c=yc, cmap="bwr", edgecolor="k")
plt.title("Linear decision boundary")
plt.show()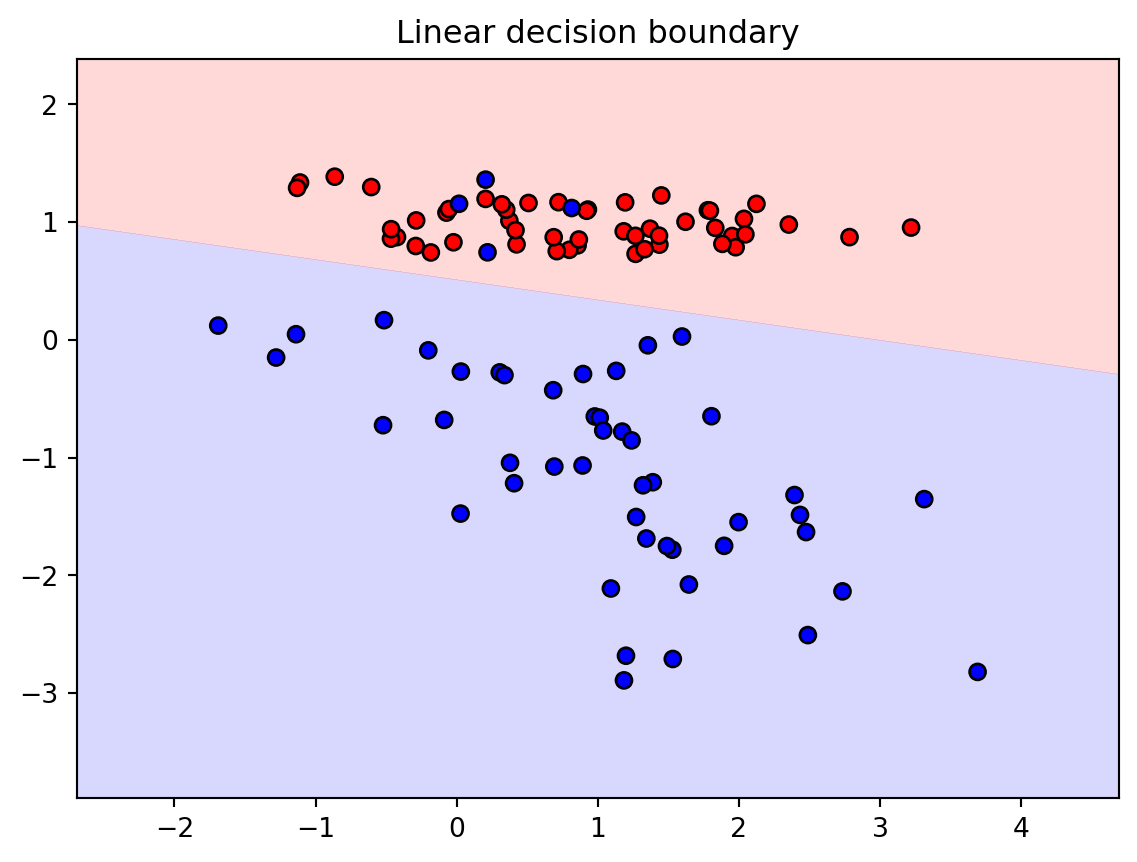

Try It Yourself

1. Add polynomial features to regression and refit. Does the line bend into a curve?
2. Change learning rate in logistic regression - what happens?
3. Generate data that is not linearly separable. Can a linear model still classify well?

The Takeaway

• Regression and classification fit naturally into linear algebra with matrix formulations.
• Least squares solves regression directly; logistic regression requires optimization.
• Linear models are simple, interpretable, and still form the foundation of modern machine learning.

96. PCA in Practice (Dimensionality Reduction Workflow)

Principal Component Analysis (PCA) is widely used to reduce dimensions, compress data, and visualize high-dimensional datasets. Here, we’ll walk through a full PCA workflow: centering, computing components, projecting, and visualizing.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

Step-by-Step Code Walkthrough

1. Load dataset (digits)

digits = load_digits()
X = digits.data  # shape (1797, 64)
y = digits.target
print("Data shape:", X.shape)

Data shape: (1797, 64)

Each sample is an 8×8 grayscale image flattened into 64 features.

2. Center the data

X_centered = X - X.mean(axis=0)

3. Compute PCA via SVD

U, S, Vt = np.linalg.svd(X_centered, full_matrices=False)
explained_variance = (S**2) / (len(X) - 1)
explained_ratio = explained_variance / explained_variance.sum()

4. Plot explained variance ratio

plt.plot(np.cumsum(explained_ratio[:30]), 'o-')
plt.xlabel("Number of components")
plt.ylabel("Cumulative explained variance")
plt.title("PCA explained variance")
plt.grid(True)
plt.show()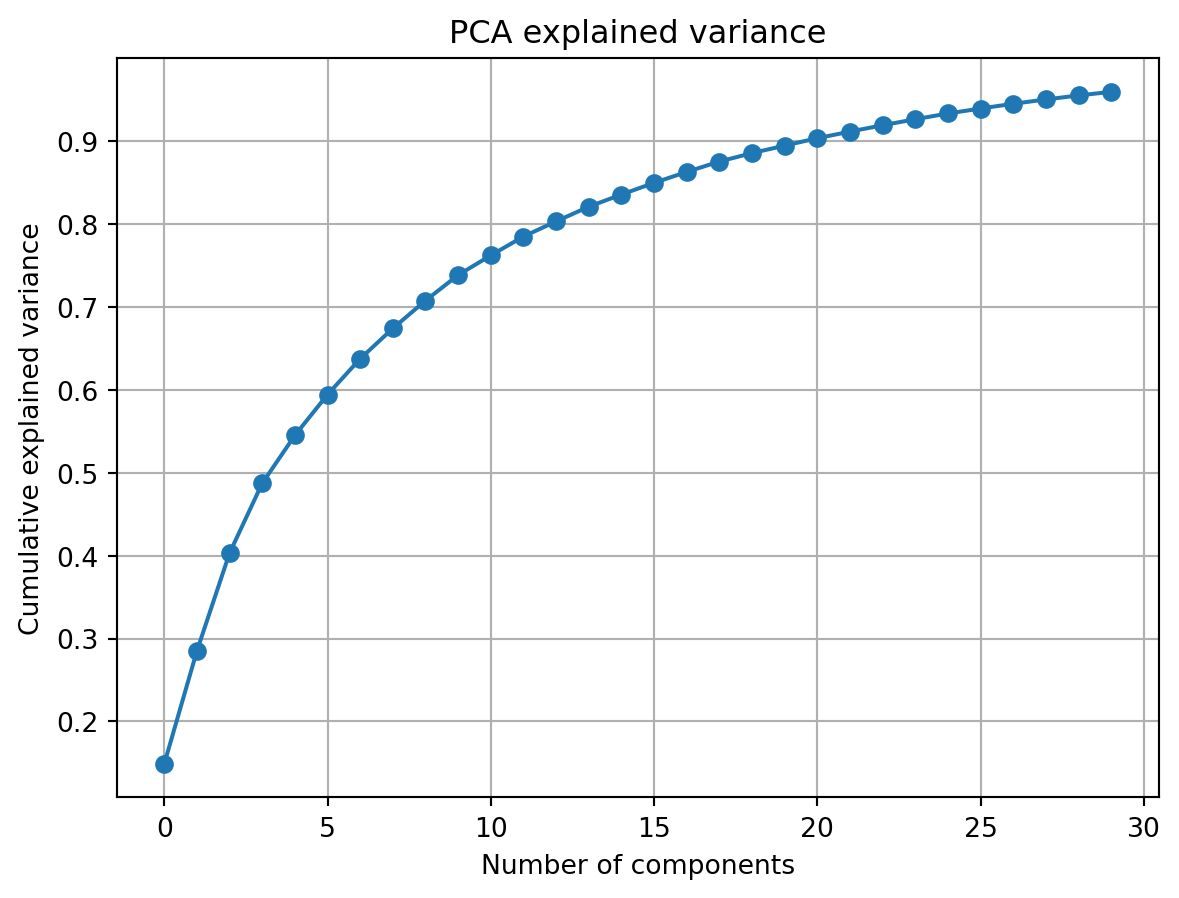

This shows how many components are needed to capture most variance.

5. Project onto top 2 components for visualization

X_pca2 = X_centered @ Vt[:2].T
plt.scatter(X_pca2[:,0], X_pca2[:,1], c=y, cmap="tab10", alpha=0.6, s=15)
plt.colorbar()
plt.title("Digits dataset (PCA 2D projection)")
plt.show()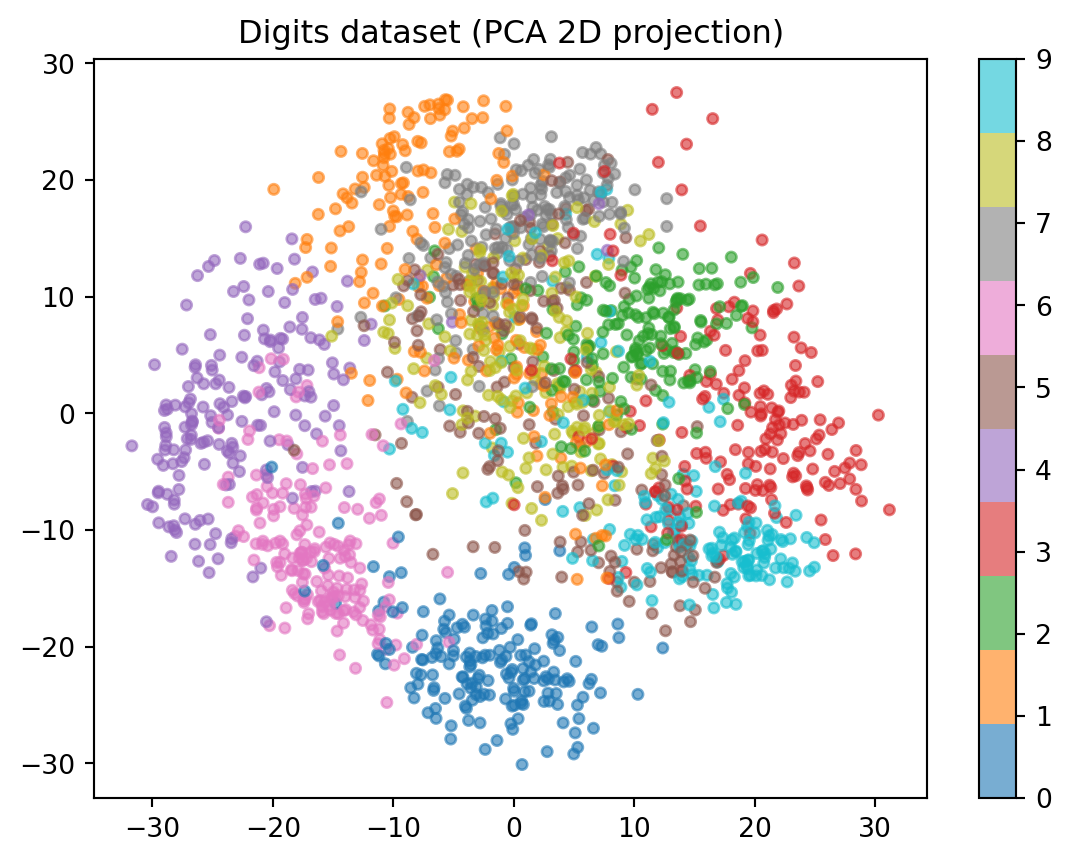

6. Reconstruct images from reduced dimensions

k = 20
X_pca20 = X_centered @ Vt[:k].T
X_reconstructed = X_pca20 @ Vt[:k]

fig, axes = plt.subplots(2, 10, figsize=(10,2))
for i in range(10):
    axes[0,i].imshow(X[i].reshape(8,8), cmap="gray")
    axes[0,i].axis("off")
    axes[1,i].imshow(X_reconstructed[i].reshape(8,8), cmap="gray")
    axes[1,i].axis("off")
plt.suptitle("Original (top) vs PCA reconstruction (bottom, 20 comps)")
plt.show()

Even with only 20/64 components, the digits remain recognizable.

Try It Yourself

1. Change \(k\) to 5, 10, 30 - how do reconstructions change?
2. Use top 2 PCA components to classify digits with k-NN. How does accuracy compare to full 64 features?
3. Try PCA on your own dataset (images, tabular data).

The Takeaway

• PCA reduces dimensions while keeping maximum variance.
• In practice: center → decompose → select top components → project/reconstruct.
• PCA enables visualization, compression, and denoising in real-world workflows.

97. Recommender Systems and Low-Rank Models (Fill the Missing Entries)

Recommender systems often deal with incomplete matrices - rows are users, columns are items, entries are ratings. Most entries are missing, but the matrix is usually close to low-rank (because user preferences depend on only a few hidden factors). SVD and low-rank approximations are powerful tools to fill in these missing values.

Set Up Your Lab

import numpy as np
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Simulate a user–item rating matrix

np.random.seed(0)
true_users = np.random.randn(10, 3)   # 10 users, 3 latent features
true_items = np.random.randn(3, 8)    # 8 items
R_full = true_users @ true_items      # true low-rank ratings

2. Hide some ratings (simulate missing data)

mask = np.random.rand(*R_full.shape) > 0.3  # keep 70% of entries
R_obs = np.where(mask, R_full, np.nan)

print("Observed ratings:\n", R_obs)

Observed ratings:
 [[-1.10781465         nan -3.56526968         nan -2.1729387   1.43510077
   1.46641178  0.79023284]
 [ 0.84819453         nan         nan         nan         nan         nan
   2.30434358  3.03008138]
 [        nan  0.32479187 -0.51818422         nan  0.02013802         nan
   1.29874918  1.33053637]
 [-1.81407786  1.24241182         nan -1.32723907         nan         nan
  -0.31110699         nan]
 [-0.48527696         nan -1.51957106         nan -0.86984941  0.52807989
          nan  0.33771451]
 [-0.26997359 -0.48498966         nan -2.73891459 -2.48167957  2.88740609
  -0.24614835         nan]
 [ 3.57769701 -1.608339    4.73789234  1.13583164  3.63451505 -2.60495928
   2.12453635  3.76472563]
 [ 0.69623809 -0.59117353 -0.28890188 -2.36431192         nan  1.50136796
   0.74268078         nan]
 [ 0.85768141  1.33357168         nan         nan  1.65089037 -2.46456289
   3.51030491  3.31220347]
 [-2.463496    0.60826298 -3.81241599 -2.11839267 -3.86597359  3.52934055
  -1.76203083 -2.63130953]]

3. Simple mean imputation (baseline)

R_mean = np.where(np.isnan(R_obs), np.nanmean(R_obs), R_obs)

4. Apply SVD for low-rank approximation

# Replace NaNs with zeros for SVD step
R_filled = np.nan_to_num(R_obs, nan=0.0)

U, S, Vt = np.linalg.svd(R_filled, full_matrices=False)

k = 3  # latent dimension
R_approx = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]

5. Compare filled matrix with ground truth

error = np.nanmean((R_full - R_approx)**2)
print("Approximation error (MSE):", error)

Approximation error (MSE): 1.4862378490976202

6. Visualize original vs reconstructed

fig, axes = plt.subplots(1, 2, figsize=(8,4))
axes[0].imshow(R_full, cmap="viridis")
axes[0].set_title("True ratings")
axes[1].imshow(R_approx, cmap="viridis")
axes[1].set_title("Low-rank approximation")
plt.show()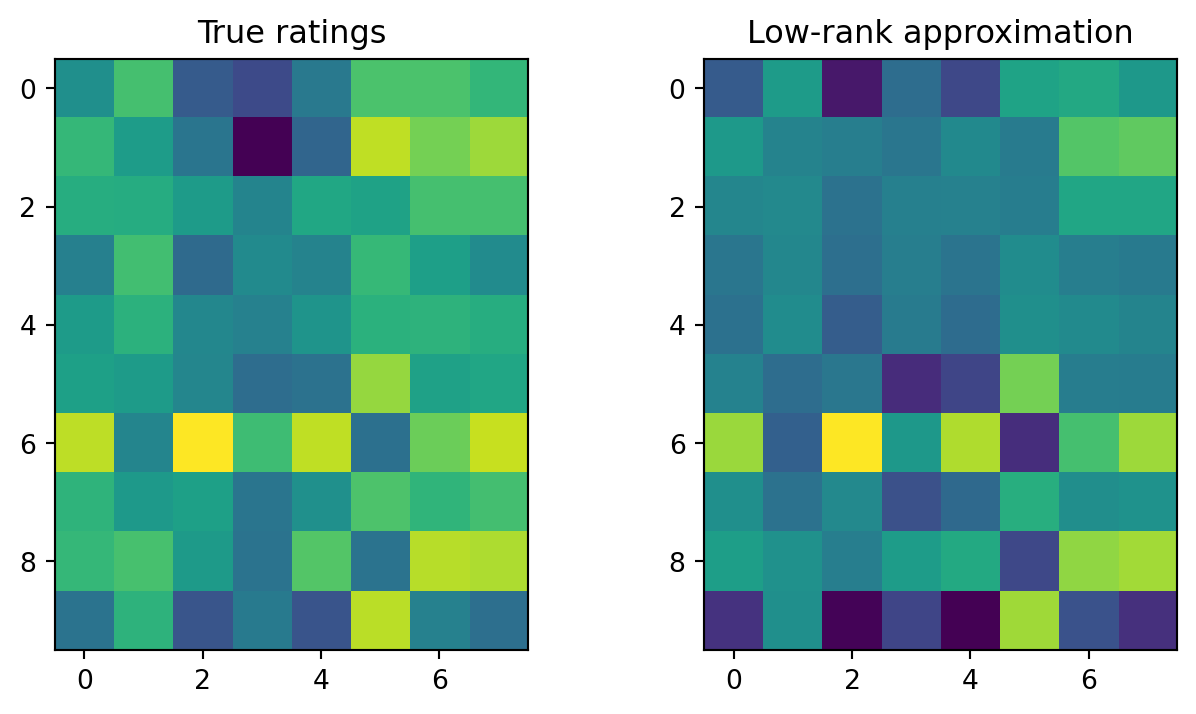

Try It Yourself

1. Vary \(k\) (2, 3, 5). Does error go down?
2. Mask more entries (50%, 80%) - how does SVD reconstruction perform?
3. Use iterative imputation: alternate filling missing entries with low-rank approximations.

The Takeaway

• Recommender systems rely on low-rank structure of user–item matrices.
• SVD provides a natural way to approximate and fill missing ratings.
• This low-rank modeling idea underpins modern collaborative filtering systems like Netflix and Spotify recommenders.

98. PageRank and Random Walks (Ranking with Eigenvectors)

The PageRank algorithm, made famous by Google, uses linear algebra and random walks on graphs to rank nodes (webpages, people, items). The idea: importance flows through links - being linked by important nodes makes you important.

The PageRank Idea

• Start a random walk on a graph: at each step, move to a random neighbor.
• Add a “teleportation” step with probability \(1 - \alpha\) to avoid dead ends.
• The steady-state distribution of this walk is the PageRank vector, found as the principal eigenvector of the transition matrix.

Set Up Your Lab

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt

Step-by-Step Code Walkthrough

1. Build a small directed graph

G = nx.DiGraph()
G.add_edges_from([
    (0,1), (1,2), (2,0),  # cycle among 0–1–2
    (2,3), (3,2),         # back-and-forth 2–3
    (1,3), (3,4), (4,1)   # small loop with 1–3–4
])
nx.draw_circular(G, with_labels=True, node_color="lightblue", node_size=800, arrowsize=15)
plt.show()

2. Build adjacency and transition matrix

n = G.number_of_nodes()
A = nx.to_numpy_array(G, nodelist=range(n))
P = A / A.sum(axis=1, keepdims=True)  # row-stochastic transition matrix

3. Add teleportation (Google matrix)

alpha = 0.85  # damping factor
G_matrix = alpha * P + (1 - alpha) * np.ones((n,n)) / n

4. Power iteration to compute PageRank

r = np.ones(n) / n  # start uniform
for _ in range(100):
    r = r @ G_matrix
r /= r.sum()
print("PageRank vector:", r)

PageRank vector: [0.13219034 0.25472358 0.24044787 0.24044787 0.13219034]

5. Compare with NetworkX built-in

pr = nx.pagerank(G, alpha=alpha)
print("NetworkX PageRank:", pr)

NetworkX PageRank: {0: 0.13219008157546333, 1: 0.2547244023837789, 2: 0.24044771723264727, 3: 0.24044771723264727, 4: 0.13219008157546333}

6. Visualize node importance

sizes = [5000 * r_i for r_i in r]
nx.draw_circular(G, with_labels=True, node_size=sizes, node_color="lightblue", arrowsize=15)
plt.title("PageRank visualization (node size ~ importance)")
plt.show()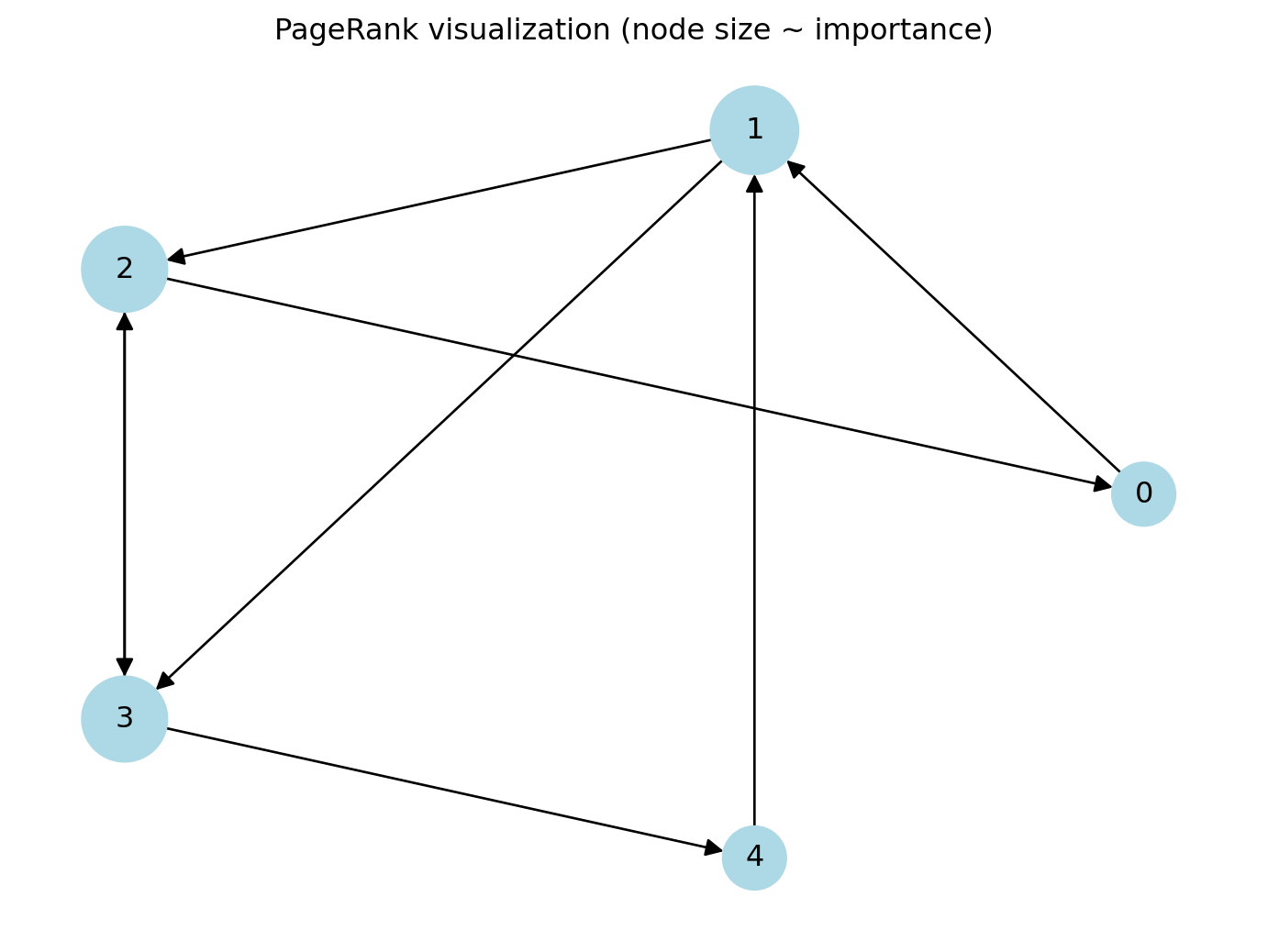

Try It Yourself

1. Change \(\alpha\) (e.g., 0.6 vs 0.95). Does ranking change?
2. Add a “dangling node” with no outlinks. How does teleportation handle it?
3. Try PageRank on a larger graph (like a random graph with 50 nodes).

The Takeaway

• PageRank is a random-walk steady state problem.
• It reduces to finding the dominant eigenvector of the Google matrix.
• This method generalizes beyond webpages - to influence ranking, recommendation, and network analysis.

99. Numerical Linear Algebra Essentials (Floating Point, BLAS/LAPACK)

When working with linear algebra on computers, numbers are not exact. They live in floating-point arithmetic, and computations rely on highly optimized libraries like BLAS and LAPACK. Understanding these essentials is crucial to doing linear algebra at scale.

Floating Point Basics

• Numbers are stored in base-2 scientific notation:

  \[ x = \pm (1.b_1b_2b_3\ldots) \times 2^e \]

• Limited precision means rounding errors.

• Two key constants:

  • Machine epsilon ($\(): smallest difference detectable (\)^{-16}$ for double).
  • Overflow/underflow: too large or too small to represent.

Set Up Your Lab

import numpy as np

Step-by-Step Code Walkthrough

1. Machine epsilon

eps = np.finfo(float).eps
print("Machine epsilon:", eps)

Machine epsilon: 2.220446049250313e-16

2. Round-off error demo

a = 1e16
b = 1.0
print("a + b - a:", (a + b) - a)  # may lose b due to precision limits

a + b - a: 0.0

3. Stability of matrix inversion

A = np.array([[1, 1.0001], [1.0001, 1]])
b = np.array([2, 2.0001])

x_direct = np.linalg.solve(A, b)
x_via_inv = np.linalg.inv(A) @ b

print("Solve:", x_direct)
print("Inverse method:", x_via_inv)

Solve: [1.499975 0.499975]
Inverse method: [1.499975 0.499975]

Notice: using np.linalg.inv can be less stable - better to solve directly.

4. Conditioning of a matrix

cond = np.linalg.cond(A)
print("Condition number:", cond)

Condition number: 20001.00000000417

• Large condition number → small input changes cause big output changes.

5. BLAS/LAPACK under the hood

A = np.random.randn(500, 500)
B = np.random.randn(500, 500)

# Matrix multiplication (calls optimized BLAS under the hood)
C = A @ B

This @ operator is not a naive loop - it calls a highly optimized C/Fortran routine.

Try It Yourself

1. Compare solving Ax = b with np.linalg.solve vs np.linalg.inv(A) @ b for larger, ill-conditioned systems.
2. Use np.linalg.svd on a nearly singular matrix. How stable are the singular values?
3. Check performance: time A @ B for sizes 100, 500, 1000.

The Takeaway

• Numerical linear algebra = math + floating-point reality.
• Always prefer stable algorithms (solve, qr, svd) over naive inversion.
• Libraries like BLAS/LAPACK make large computations fast, but understanding precision and conditioning prevents nasty surprises.

100. Capstone Problem Sets and Next Steps (A Roadmap to Mastery)

This final section ties everything together. Instead of introducing a new topic, it provides capstone labs that combine multiple ideas from the book. Working through them will give you confidence that you can apply linear algebra to real problems.

Problem Set 1 - Image Compression with SVD

Take an image, treat it as a matrix, and approximate it with low-rank SVD.

import numpy as np
import matplotlib.pyplot as plt
from skimage import data, color

# Load grayscale image
img = color.rgb2gray(data.astronaut())
U, S, Vt = np.linalg.svd(img, full_matrices=False)

# Approximate with rank-k
k = 50
img_approx = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]

plt.subplot(1,2,1)
plt.imshow(img, cmap="gray")
plt.title("Original")
plt.axis("off")

plt.subplot(1,2,2)
plt.imshow(img_approx, cmap="gray")
plt.title(f"Rank-{k} Approximation")
plt.axis("off")

plt.show()

Try different \(k\) values (5, 20, 100). How does quality vs. compression trade off?

Problem Set 2 - Predictive Modeling with PCA + Regression

Combine PCA for dimensionality reduction with linear regression for prediction.

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.decomposition import PCA

# Load dataset
X, y = load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# PCA reduce features
pca = PCA(n_components=5)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)

# Regression on reduced space
model = LinearRegression().fit(X_train_pca, y_train)
print("R^2 on test set:", model.score(X_test_pca, y_test))

R^2 on test set: 0.3691398497153573

Does reducing dimensions improve or hurt accuracy?

Problem Set 3 - Graph Analysis with PageRank

Apply PageRank to a custom-built network.

import networkx as nx

G = nx.barabasi_albert_graph(20, 2)  # 20 nodes, scale-free graph
pr = nx.pagerank(G, alpha=0.85)

nx.draw(G, with_labels=True, node_size=[5000*pr[n] for n in G], node_color="lightblue")
plt.title("PageRank on a scale-free graph")
plt.show()

Which nodes dominate? How does structure affect ranking?

Problem Set 4 - Solving Differential Equations with Eigen Decomposition

Use eigenvalues/eigenvectors to solve a linear dynamical system.

A = np.array([[0,1],[-2,-3]])
eigvals, eigvecs = np.linalg.eig(A)

print("Eigenvalues:", eigvals)
print("Eigenvectors:\n", eigvecs)

Eigenvalues: [-1. -2.]
Eigenvectors:
 [[ 0.70710678 -0.4472136 ]
 [-0.70710678  0.89442719]]

Predict long-term behavior: will the system decay, oscillate, or grow?

Problem Set 5 - Least Squares for Overdetermined Systems

np.random.seed(0)
X = np.random.randn(100, 3)
beta_true = np.array([2, -1, 0.5])
y = X @ beta_true + np.random.randn(100)*0.1

beta_hat, *_ = np.linalg.lstsq(X, y, rcond=None)
print("Estimated coefficients:", beta_hat)

Estimated coefficients: [ 1.99371939 -1.00708947  0.50661857]

Compare estimated vs. true coefficients. How close are they?

Try It Yourself

1. Combine SVD and recommender systems - build a movie recommender with synthetic data.
2. Implement Gram–Schmidt by hand and test it against np.linalg.qr.
3. Write a mini “linear algebra toolkit” with your favorite helper functions.

The Takeaway

• You’ve practiced vectors, matrices, systems, eigenvalues, SVD, PCA, PageRank, and more.
• Real problems often combine multiple concepts - the labs show how everything fits together.
• Next steps: dive deeper into numerical linear algebra, explore machine learning applications, or study advanced matrix factorizations (Jordan form, tensor decompositions).

This concludes the hands-on journey. By now, you don’t just know the theory - you can use linear algebra as a working tool in Python for data, science, and engineering.